Java C++ 算法题解leetcode669修剪二叉搜索树示例

目录

• 题目要求
• 思路一：模拟迭代
• Java
• C++
• 思路二：递归
• Java
• C++
• Rust

题目要求

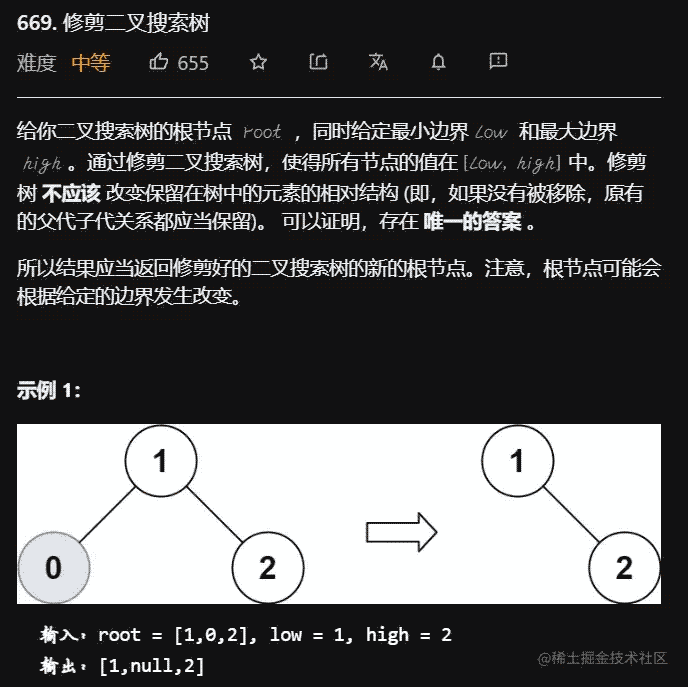
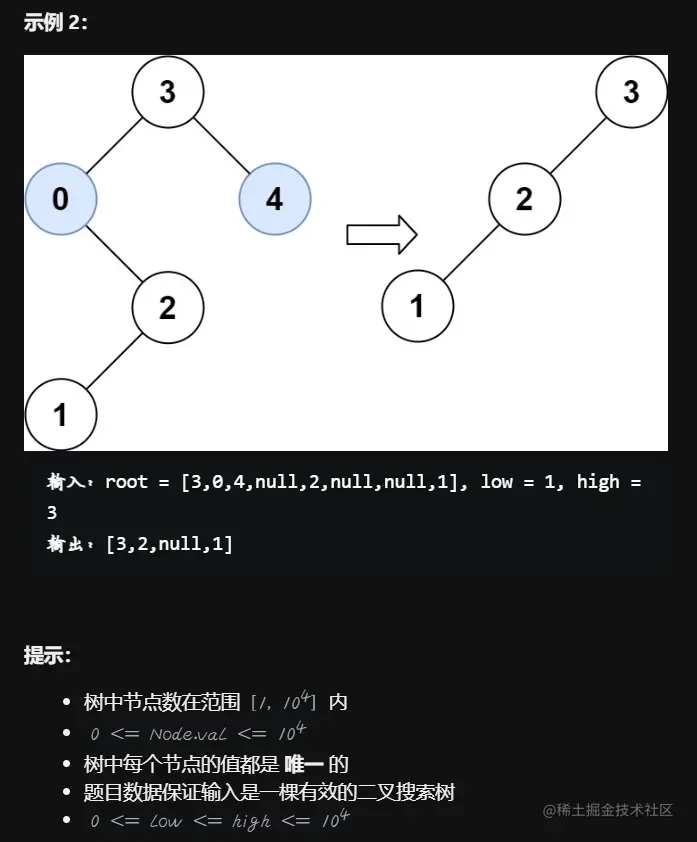
思路一：模拟迭代

• 依次判断每个节点是否合法：
  • 首先找出结果的根，若原根小了就拉右边的过来，大了拉左边的过来做新根；
  • 然后分别判断左右子树的大小，由于二叉搜索树的性质，子树只需要判断一边就好：
    • 左子树判断是否>low，合法就向左下走，不合法往右下；
    • 右子树判断是否<high，合法就向右下走，不合法往左下。

Java

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        while (root != null && (root.val < low || root.val > high)) // 确定原根是否合法
            root = root.val < low ? root.right : root.left;
        TreeNode res = root;
        while (root != null) {
            while (root.left != null && root.left.val < low)
                root.left = root.left.right;
            root = root.left;
        }
        root = res;
        while (root != null) {
            while (root.right != null && root.right.val > high)
                root.right = root.right.left;
            root = root.right;
        }
        return res;
    }
}

• 时间复杂度：O(n)
• 空间复杂度：O(1)

C++

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        while (root != nullptr && (root->val < low || root->val > high)) // 确定原根是否合法
            root = root->val < low ? root->right : root->left;
        TreeNode* res = root;
        while (root != nullptr) {
            while (root->left != nullptr && root->left->val < low)
                root->left = root->left->right;
            root = root->left;
        }
        root = res;
        while (root != nullptr) {
            while (root->right != nullptr && root->right->val > high)
                root->right = root->right->left;
            root = root->right;
        }
        return res;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

思路二：递归

• 直接用当前函数递归修剪即可：
  • 当前值小了放右下（大）的值进去，剪掉当前和左边节点；
  • 当前值大了放左下（小）的值进去，剪掉当前和右边节点。
  • 然后递归掉下面所有节点。

Java

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null)
            return null;
        if (root.val < low)
            return trimBST(root.right, low, high);
        else if (root.val > high)
            return trimBST(root.left, low, high);
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

• 时间复杂度：O(n)
• 空间复杂度：O(1)，忽略递归的额外空间开销

C++

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr)
            return nullptr;
        if (root->val < low)
            return trimBST(root->right, low, high);
        else if (root->val > high)
            return trimBST(root->left, low, high);
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)，忽略递归的额外空间开销

Rust

• 今天又见识到了新报错：already borrowed: BorrowMutError，不能把borrow的东西来回随便等，要搞临时中间变量，闭包要关好。

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn trim_bst(root: Option<Rc<RefCell<TreeNode>>>, low: i32, high: i32) -> Option<Rc<RefCell<TreeNode>>> {
        if  root.is_none() {
            return None;
        }
        if root.as_ref().unwrap().borrow().val < low {
            return Solution::trim_bst(root.as_ref().unwrap().borrow().right.clone(), low, high);
        }
        else if root.as_ref().unwrap().borrow().val > high {
            return Solution::trim_bst(root.as_ref().unwrap().borrow().left.clone(), low, high);
        }
        let (l, r) = (Solution::trim_bst(root.as_ref().unwrap().borrow().left.clone(), low, high), Solution::trim_bst(root.as_ref().unwrap().borrow().right.clone(), low, high)); // 要先拎出来
        root.as_ref().unwrap().borrow_mut().left = l;
        root.as_ref().unwrap().borrow_mut().right = r;
        root
    }
}

• 时间复杂度：O(n)
• 空间复杂度：O(1)，忽略递归的额外空间开销

以上就是Java C++ 算法题解leetcode669修剪二叉搜索树的详细内容，更多关于Java C++ 算法修剪二叉搜索树的资料请关注我们其它相关文章！