详解js数组的完全随机排列算法

Array.prototype.sort 方法被许多 JavaScript 程序员误用来随机排列数组。最近做的前端星计划挑战项目中，一道实现 blackjack 游戏的问题，就发现很多同学使用了 Array.prototype.sort 来洗牌。

洗牌

以下就是常见的完全错误的随机排列算法：

function shuffle(arr){
 return arr.sort(function(){
 return Math.random() - 0.5;
 });
}

以上代码看似巧妙利用了 Array.prototype.sort 实现随机，但是，却有非常严重的问题，甚至是完全错误。

证明 Array.prototype.sort 随机算法的错误

为了证明这个算法的错误，我们设计一个测试的方法。假定这个排序算法是正确的，那么，将这个算法用于随机数组 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]，如果算法正确，那么每个数字在每一位出现的概率均等。因此，将数组重复洗牌足够多次，然后将每次的结果在每一位相加，最后对每一位的结果取平均值，这个平均值应该约等于 (0 + 9) / 2 = 4.5，测试次数越多次，每一位上的平均值就都应该越接近于 4.5。所以我们简单实现测试代码如下：

var arr = [0,1,2,3,4,5,6,7,8,9];
var res = [0,0,0,0,0,0,0,0,0,0];
var t = 10000;
for(var i = 0; i < t; i++){
 var sorted = shuffle(arr.slice(0));
 sorted.forEach(function(o,i){
 res[i] += o;
 });
}
res = res.map(function(o){
 return o / t;
});
console.log(res);

将上面的 shuffle 方法用这段测试代码在 chrome 浏览器中测试一下，可以得出结果，发现结果并不随机分布，各个位置的平均值越往后越大，这意味着这种随机算法越大的数字出现在越后面的概率越大。

为什么会产生这个结果呢？我们需要了解 Array.prototype.sort 究竟是怎么作用的。

首先我们知道排序算法有很多种，而 ECMAScript 并没有规定 Array.prototype.sort 必须使用何种排序算法。

排序不是我们今天讨论的主题，但是不论用何种排序算法，都是需要进行两个数之间的比较和交换，排序算法的效率和两个数之间比较和交换的次数有关系。

最基础的排序有冒泡排序和插入排序，原版的冒泡或者插入排序都比较了 n(n-1)/2 次，也就是说任意两个位置的元素都进行了一次比较。那么在这种情况下，如果采用前面的 sort 随机算法，由于每次比较都有 50% 的几率交换和不交换，这样的结果是随机均匀的吗？我们可以看一下例子：

function bubbleSort(arr, compare){
 var len = arr.length;
 for(var i = 0; i < len - 1; i++){
 for(var j = 0; j < len - 1 - i; j++){
 var k = j + 1;
 if(compare(arr[j], arr[k]) > 0){
 var tmp = arr[j];
 arr[j] = arr[k];
 arr[k] = tmp;
 }
 }
 }
 return arr;
}
function shuffle(arr){
 return bubbleSort(arr, function(){
 return Math.random() - 0.5;
 });
}
var arr = [0,1,2,3,4,5,6,7,8,9];
var res = [0,0,0,0,0,0,0,0,0,0];
var t = 10000;
for(var i = 0; i < t; i++){
 var sorted = shuffle(arr.slice(0));
 sorted.forEach(function(o,i){
 res[i] += o;
 });
}
res = res.map(function(o){
 return o / t;
});
console.log(res);

上面的代码的随机结果也是不均匀的，测试平均值的结果越往后的越大。（笔者之前没有复制原数组所以错误得出均匀的结论，已更正于 2016-05-10）

冒泡排序总是将比较结果较小的元素与它的前一个元素交换，我们可以大约思考一下，这个算法越后面的元素，交换到越前的位置的概率越小（因为每次只有50%几率“冒泡”），原始数组是顺序从小到大排序的，因此测试平均值的结果自然就是越往后的越大（因为越靠后的大数出现在前面的概率越小）。

我们再换一种算法，我们这一次用插入排序：

function insertionSort(arr, compare){
 var len = arr.length;
 for(var i = 0; i < len; i++){
 for(var j = i + 1; j < len; j++){
 if(compare(arr[i], arr[j]) > 0){
 var tmp = arr[i];
 arr[i] = arr[j];
 arr[j] = tmp;
 }
 }
 }
 return arr;
}
function shuffle(arr){
 return insertionSort(arr, function(){
 return Math.random() - 0.5;
 });
}
var arr = [0,1,2,3,4,5,6,7,8,9];
var res = [0,0,0,0,0,0,0,0,0,0];
var t = 10000;
for(var i = 0; i < t; i++){
 var sorted = shuffle(arr.slice(0));
 sorted.forEach(function(o,i){
 res[i] += o;
 });
}
res = res.map(function(o){
 return o / t;
});
console.log(res);

由于插入排序找后面的大数与前面的数进行交换，这一次的结果和冒泡排序相反，测试平均值的结果自然就是越往后越小。原因也和上面类似，对于插入排序，越往后的数字越容易随机交换到前面。

所以我们看到即使是两两交换的排序算法，随机分布差别也是比较大。除了每个位置两两都比较一次的这种排序算法外，大多数排序算法的时间复杂度介于 O(n) 到 O(n2) 之间，元素之间的比较次数通常情况下要远小于 n(n-1)/2，也就意味着有一些元素之间根本就没机会相比较（也就没有了随机交换的可能），这些 sort 随机排序的算法自然也不能真正随机。

我们将上面的代码改一下，采用快速排序：

function quickSort(arr, compare){
 arr = arr.slice(0);
 if(arr.length <= 1) return arr;
 var mid = arr[0], rest = arr.slice(1);
 var left = [], right = [];
 for(var i = 0; i < rest.length; i++){
 if(compare(rest[i], mid) > 0){
 right.push(rest[i]);
 }else{
 left.push(rest[i]);
 }
 }
 return quickSort(left, compare).concat([mid])
 .concat(quickSort(right, compare));
}
function shuffle(arr){
 return quickSort(arr, function(){
 return Math.random() - 0.5;
 });
}
var arr = [0,1,2,3,4,5,6,7,8,9];
var res = [0,0,0,0,0,0,0,0,0,0];
var t = 10000;
for(var i = 0; i < t; i++){
 var sorted = shuffle(arr.slice(0));
 sorted.forEach(function(o,i){
 res[i] += o;
 });
}
res = res.map(function(o){
 return o / t;
});
console.log(res);

快速排序并没有两两元素进行比较，它的概率分布也不随机。

所以我们可以得出结论，用 Array.prototype.sort 随机交换的方式来随机排列数组，得到的结果并不一定随机，而是取决于排序算法是如何实现的，用 JavaScript 内置的排序算法这么排序，通常肯定是不完全随机的。

经典的随机排列

所有空间复杂度 O(1) 的排序算法的时间复杂度都介于 O(nlogn) 到 O(n2) 之间，因此在不考虑算法结果错误的前提下，使用排序来随机交换也是慢的。事实上，随机排列数组元素有经典的 O(n) 复杂度的算法：

function shuffle(arr){
 var len = arr.length;
 for(var i = 0; i < len - 1; i++){
 var idx = Math.floor(Math.random() * (len - i));
 var temp = arr[idx];
 arr[idx] = arr[len - i - 1];
 arr[len - i -1] = temp;
 }
 return arr;
}

在上面的算法里，我们每一次循环从前 len - i 个元素里随机一个位置，将这个元素和第 len - i 个元素进行交换，迭代直到 i = len - 1 为止。

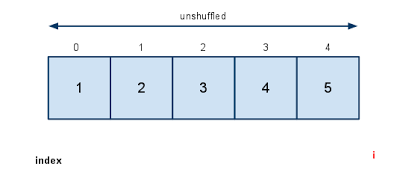
我们同样可以检验一下这个算法的随机性：

function shuffle(arr){
 var len = arr.length;
 for(var i = 0; i < len - 1; i++){
 var idx = Math.floor(Math.random() * (len - i));
 var temp = arr[idx];
 arr[idx] = arr[len - i - 1];
 arr[len - i -1] = temp;
 }
 return arr;
}
var arr = [0,1,2,3,4,5,6,7,8,9];
var res = [0,0,0,0,0,0,0,0,0,0];
var t = 10000;
for(var i = 0; i < t; i++){
 var sorted = shuffle(arr.slice(0));
 sorted.forEach(function(o,i){
 res[i] += o;
 });
}
res = res.map(function(o){
 return o / t;
});
console.log(res);

从结果可以看出这个算法的随机结果应该是均匀的。不过我们的测试方法其实有个小小的问题，我们只测试了平均值，实际上平均值接近只是均匀分布的必要而非充分条件，平均值接近不一定就是均匀分布。不过别担心，事实上我们可以简单从数学上证明这个算法的随机性。

随机性的数学归纳法证明

对 n 个数进行随机：

首先我们考虑 n = 2 的情况，根据算法，显然有 1/2 的概率两个数交换，有 1/2 的概率两个数不交换，因此对 n = 2 的情况，元素出现在每个位置的概率都是 1/2，满足随机性要求。

假设有 i 个数， i >= 2 时，算法随机性符合要求，即每个数出现在 i 个位置上每个位置的概率都是 1/i。

对于 i + 1 个数，按照我们的算法，在第一次循环时，每个数都有 1/(i+1) 的概率被交换到最末尾，所以每个元素出现在最末一位的概率都是 1/(i+1) 。而每个数也都有 i/(i+1) 的概率不被交换到最末尾，如果不被交换，从第二次循环开始还原成 i 个数随机，根据 2. 的假设，它们出现在 i 个位置的概率是 1/i。因此每个数出现在前 i 位任意一位的概率是 (i/(i+1)) * (1/i) = 1/(i+1)，也是 1/(i+1)。

综合 1. 2. 3. 得出，对于任意 n >= 2，经过这个算法，每个元素出现在 n 个位置任意一个位置的概率都是 1/n。

总结

一个优秀的算法要同时满足结果正确和高效率。很不幸使用 Array.prototype.sort 方法这两个条件都不满足。因此，当我们需要实现类似洗牌的功能的时候，还是应该采用巧妙的经典洗牌算法，它不仅仅具有完全随机性还有很高的效率。

除了收获这样的算法之外，我们还应该认真对待这种动手分析和解决问题的思路，并且捡起我们曾经学过而被大多数人遗忘的数学（比如数学归纳法这种经典的证明方法）。

有任何问题欢迎与作者探讨~

以上就是本文的全部内容，希望本文的内容对大家的学习或者工作能带来一定的帮助，同时也希望多多支持我们！