java图搜索算法之DFS与BFS详解

目录
  • 一、前言
  • 二、深度优先搜索
  • 三、广度优先搜索
  • 四、结语

你好，我是小黄，一名独角兽企业的Java开发工程师。
感谢茫茫人海中我们能够相遇，
俗话说：当你的才华和能力，不足以支撑你的梦想的时候，请静下心来学习，
希望优秀的你可以和我一起学习，一起努力，实现属于自己的梦想。

一、前言

上一篇文章我们提到了关于图的形象化描述方法，不知道大家还有没有印象。没有印象的话，可以去看一下上期的内容

对于图来说，搜索的方法无外乎两种，深度优先搜索（DFS）和广度优先搜索（BFS）

两种搜索算法也不太相同，今天我们就来看一下这两个搜索算法

二、深度优先搜索

我们一提到深度优先搜索，脑子里第一时间想到的就是递归

没错，深搜就是依靠递归的方法来进行的搜索，我们来看一个例题：

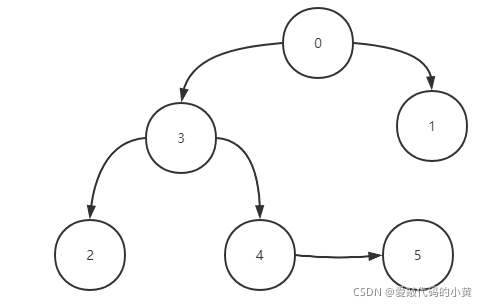
对于上图来说，使用深度优先搜索的路线为：0 -> 3 - > 2 -> 4 -> 5 -> 1

这里不懂深搜的小伙伴可以看下这篇：深度优先搜索

递归版本：

	/**
     * 深度优先搜索
     *
     * @param node
     * @param set
     */
	public void DFS(Node node, Set<Node> set) {
        if (node == null) {
            return;
        }
        if (!set.contains(node)) {
            set.add(node);
            System.out.print(node.value + " ");
            for (Node node1 : node.nexts) {
                DFS(node1, set);
            }
        }
    }

迭代版本：

	/**
     * 深度优先搜索
     *
     * @param node
     */
	public void DFS(Node node) {
        Stack<Node> stack = new Stack<>();
        Set<Node> set = new HashSet<>();
        stack.add(node);
        set.add(node);
        System.out.print(node.value + " ");
        while (!stack.isEmpty()) {
            Node cur = stack.pop();
            for (Node next : cur.nexts) {
                if (!set.contains(next)) {
                    stack.add(cur); // 用来做记忆化的
                    stack.add(next);
                    System.out.print(next.value + " ");
                    set.add(next);
                    break;
                }
            }
        }
    }

测试结果：

迭代版本：
0 3 2 4 5 1
递归版本：
0 3 2 4 5 1

三、广度优先搜索

对于广度优先搜索的话，简单的来说，像走地图一样，一圈一圈的扩展开来

我们来看一个例题：

对于上图来说，使用深度优先搜索的路线为：0 -> 3 -> 1 -> 2 -> 4 -> 5

这里不懂广搜的小伙伴可以看下这篇：广度优先搜索

	/**
     * 广度优先搜索
     *
     * @param node
     */
    public static void BFS(Node node) {
        if (node == null) {
            return;
        }
        Queue<Node> queue = new LinkedList<>();
        // 代表是否被使用
        Set<Node> set = new HashSet<>();
        queue.add(node);
        set.add(node);
        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            System.out.print(cur.value + " ");
            for (Node next : cur.nexts) {
                if (!set.contains(next)) {
                    queue.add(next);
                    set.add(next);
                }
            }
        }
    }

四、结语

这期的深度优先搜索和广度优先搜索比较简单

让你对图的搜索大概有个了解，下几期将会讲解一些真实的算法

在算法题中，题目不会单纯的让你求深搜和广搜，经常会和别的一起出现，比如最小生成树等

以上就是java数据结构图算法之DFS与BFS详解的详细内容，更多关于java数据结构图算法DFS与BFS的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • Java经典排序算法之归并排序详解

    Java经典排序算法之归并排序详解

    一.归并排序 归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用.将已有序的子序列合并,得到完全有序的序列:即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,称为二路归并. 归并过程为:比较a[i]和a[j]的大小,若a[i]≤a[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1:否则将第二个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直

  • Java实现利用广度优先遍历(BFS)计算最短路径的方法

    Java实现利用广度优先遍历(BFS)计算最短路径的方法

    本文实例讲述了Java实现利用广度优先遍历(BFS)计算最短路径的方法.分享给大家供大家参考.具体分析如下: 我们用字符串代表图的顶点(vertax),来模拟学校中Classroom, Square, Toilet, Canteen, South Gate, North Gate几个地点,然后计算任意两点之间的最短路径. 如下图所示: 如,我想从North Gate去Canteen, 程序的输出结果应为: BFS: From [North Gate] to [Canteen]: North Ga

  • Java编程实现深度优先遍历与连通分量代码示例

    Java编程实现深度优先遍历与连通分量代码示例

    深度优先遍历 深度优先遍历类似于一个人走迷宫: 如图所示,从起点开始选择一条边走到下一个顶点,没到一个顶点便标记此顶点已到达. 当来到一个标记过的顶点时回退到上一个顶点,再选择一条没有到达过的顶点. 当回退到的路口已没有可走的通道时继续回退. 而连通分量,看概念:无向图G的极大连通子图称为G的连通分量( Connected Component).任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量. 下面看看具体实例: package com.dataStructure.gra

  • Java编程实现基于图的深度优先搜索和广度优先搜索完整代码

    Java编程实现基于图的深度优先搜索和广度优先搜索完整代码

    为了解15puzzle问题,了解了一下深度优先搜索和广度优先搜索.先来讨论一下深度优先搜索(DFS),深度优先的目的就是优先搜索距离起始顶点最远的那些路径,而广度优先搜索则是先搜索距离起始顶点最近的那些路径.我想着深度优先搜索和回溯有什么区别呢?百度一下,说回溯是深搜的一种,区别在于回溯不保留搜索树.那么广度优先搜索(BFS)呢?它有哪些应用呢?答:最短路径,分酒问题,八数码问题等.言归正传,这里笔者用java简单实现了一下广搜和深搜.其中深搜是用图+栈实现的,广搜使用图+队列实现的,代码如下:

  • java图搜索算法之DFS与BFS详解

    java图搜索算法之DFS与BFS详解

    目录 一.前言 二.深度优先搜索 三.广度优先搜索 四.结语 你好,我是小黄,一名独角兽企业的Java开发工程师. 感谢茫茫人海中我们能够相遇, 俗话说:当你的才华和能力,不足以支撑你的梦想的时候,请静下心来学习, 希望优秀的你可以和我一起学习,一起努力,实现属于自己的梦想. 一.前言 上一篇文章我们提到了关于图的形象化描述方法,不知道大家还有没有印象.没有印象的话,可以去看一下上期的内容 对于图来说,搜索的方法无外乎两种,深度优先搜索(DFS)和广度优先搜索(BFS) 两种搜索算法也不太相同,

  • Java 数据结构算法Collection接口迭代器示例详解

    Java 数据结构算法Collection接口迭代器示例详解

    目录 Java合集框架 Collection接口 迭代器 Java合集框架 数据结构是以某种形式将数据组织在一起的合集(collection).数据结构不仅存储数据,还支持访问和处理数据的操作 在面向对象的思想里,一种数据结构也被认为是一个容器(container)或者容器对象(container object),它是一个能存储其他对象的对象,这里的其他对象常被称为数据或者元素 定义一种数据结构从实质上讲就是定义一个类.数据结构类应该使用数据域存储数据,并提供方法支持查找.插入和删除等操作 Ja

  • Java笛卡尔积算法原理与实现方法详解

    Java笛卡尔积算法原理与实现方法详解

    本文实例讲述了Java笛卡尔积算法原理与实现方法.分享给大家供大家参考,具体如下: 笛卡尔积算法的Java实现: (1)循环内,每次只有一列向下移一个单元格,就是CounterIndex指向的那列. (2)如果该列到尾部了,则这列index重置为0,而CounterIndex则指向前一列,相当于进位,把前列的index加一. (3)最后,由生成的行数来控制退出循环. public class Test { private static String[] aa = { "aa1", &q

  • Java 蒙特卡洛算法求圆周率近似值实例详解

    起源 [1946: John von Neumann, Stan Ulam, and Nick Metropolis, all at the Los Alamos Scientific Laboratory, cook up the Metropolis algorithm, also known as the Monte Carlo method.]1946年,美国拉斯阿莫斯国家实验室的三位科学家John von Neumann,Stan Ulam 和 Nick Metropolis共同发明,

  • java编程无向图结构的存储及DFS操作代码详解

    java编程无向图结构的存储及DFS操作代码详解

    图的概念 图是算法中是树的拓展,树是从上向下的数据结构,结点都有一个父结点(根结点除外),从上向下排列.而图没有了父子结点的概念,图中的结点都是平等关系,结果更加复杂. 无向图                                                       有向图 图G=(V,E),其中V代表顶点Vertex,E代表边edge,一条边就是一个定点对(u,v),其中(u,v)∈V. 这两天遇到一个关于图的算法,在网上找了很久没有找到java版的关于数据结构中图的存储及其

  • Go Java算法之单词搜索示例详解

    Go Java算法之单词搜索示例详解

    目录 单词搜索 算法:DFS回溯(Java) 算法:DFS回溯(Go) 单词搜索 给定一个 m x n 二维字符网格 board 和一个字符串单词 word .如果 word 存在于网格中,返回 true :否则,返回 false . 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格.同一个单元格内的字母不允许被重复使用. 示例 1: 输入:board = [["A","B","C",&quo

  • Go Java算法之累加数示例详解

    目录 累加数 方法一:穷举法(java) 方法二:深度优先遍历(go) 累加数 累加数 是一个字符串,组成它的数字可以形成累加序列. 一个有效的 累加序列 必须 至少 包含 3 个数.除了最开始的两个数以外,序列中的每个后续数字必须是它之前两个数字之和. 给你一个只包含数字 '0'-'9' 的字符串,编写一个算法来判断给定输入是否是 累加数 .如果是,返回 true :否则,返回 false . 说明:累加序列里的数,除数字 0 之外,不会 以 0 开头,所以不会出现 1, 2, 03 或者 1

  • Java中Prime算法的原理与实现详解

    Java中Prime算法的原理与实现详解

    目录 Prim算法介绍 1.点睛 2.算法介绍 3. 算法步骤 4.图解 Prime 算法实现 1.构建后的图 2.代码 3.测试 Prim算法介绍 1.点睛 在生成树的过程中,把已经在生成树中的节点看作一个集合,把剩下的节点看作另外一个集合,从连接两个集合的边中选择一条权值最小的边即可. 2.算法介绍 首先任选一个节点,例如节点1,把它放在集合 U 中,U={1},那么剩下的节点为 V-U={2,3,4,5,6,7},集合 V 是图的所有节点集合. 现在只需要看看连接两个集合(U 和 V-U)

  • Go Java算法之交错字符串示例详解

    目录 交错字符串 方法一:动态规划(Java) 方法一:动态规划(GO) 交错字符串 给定三个字符串 s1.s2.s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的. 两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串: s = s1 + s2 + ... + sn t = t1 + t2 + ... + tm |n - m| <= 1 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 +

  • Go Java算法之比较版本号方法详解

    目录 比较版本号 方法一:字符串切割(Java) 方法二:双指针(Go) 比较版本号 给你两个版本号 version1 和 version2 ,请你比较它们. 版本号由一个或多个修订号组成,各修订号由一个 '.' 连接.每个修订号由 多位数字 组成,可能包含 前导零 .每个版本号至少包含一个字符. 修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推.例如,2.5.33 和 0.1 都是有效的版本号. 比较版本号时,请按从左到右的顺序依次比较它们的

随机推荐