C++详解哈夫曼树的概念与实现步骤

目录

• 一、 基本概念
• 二、构造哈夫曼树
• 三、哈夫曼树的基本性质
• 四、哈夫曼编码
• 五、哈夫曼解码
• 六、文件的压缩和解压缩

一、 基本概念

结点的权： 有某种现实含义的数值

结点的带权路径长度： 从结点的根到该结点的路径长度与该结点权值的乘积

树的带权路径长度： 树上所有叶结点的带权路径长度之和

哈夫曼树： 在含有 n n n个带权叶结点的二叉树中， w p l wpl wpl 最小 的二叉树称为哈夫曼树，也称最优二叉树（给定叶子结点，哈夫曼树不唯一）。

二、构造哈夫曼树

比较简单，此处不赘述步骤

三、哈夫曼树的基本性质

• 每个初始结点最终都是叶结点，且权值越小的结点到根结点的路径长度越大
• 具有 n n n个根结点的哈夫曼树的结点总数为 2 n − 1
• 哈夫曼树中不存在度为1的结点
• 哈夫曼树不唯一，但 w p l必然相同且最优

四、哈夫曼编码

目的：为给定的字符集合构建二进制编码，使得编码的期望长度达到最短

在考试中，小渣利用哈夫曼编码老渣发电报传递100道选择题的答案，小渣传递了10个A、8个B、80个C、2个D，老渣利用哈夫曼编码的方式解码。

小渣构造的哈夫曼树如下：

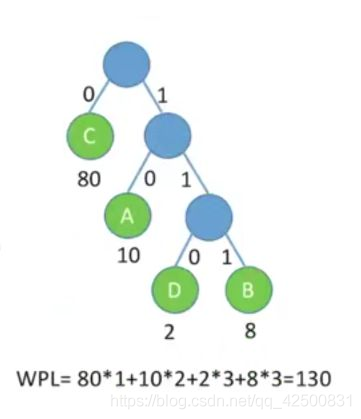
可以发现，A、B、C、D的编码分别为10、111、0、110。

这样小渣只要根据1~100题的答案顺序发送01序列，老渣收到后进行解码就能正确收到答案了。而且哈夫曼编码的方式不会有歧义，因为哈夫曼编码是一种前缀编码。

前缀编码： 没有一个编码是另一个编码的前缀，因为数据节点都是叶子节点。如果出现一个字符的编码是另一个字符编码的前缀，那这个字符一定处于内部节点，这是不可能的

由哈夫曼树得到的哈夫曼编码： 字符集中的每个字符都是以叶子结点出现在哈夫曼树中，各个字符出现的频率为结点的权值。

给字符串进行编码的时候，由于出现频率越高（权值大）的字符距离根节点越进，编码越短；只有出现频率越低（权值小）的字符距离根节点较远，编码长。没关系，由于频率高的字符编码都短，所以哈夫曼编码可以得到最短的编码序列

五、哈夫曼解码

哈夫曼编码不同于ASCII和Unicode这些字符编码，这些字符集中的码长都采用的是长度相同的编码方案，而哈夫曼编码使用的是变长编码，而且哈夫曼编码满足立刻可解码性（就是说任一字符的编码都不会是另一个更长字符编码的前缀），只要当某个字符的编码中所有位被全部接收时，可以立即进行解码而无须等待后面接收的位来决定是否存在另一个合法的更长的编码

第一张表不满足立刻可解码性，第二张表满足

我们接收100的时候，需要考虑是立刻解码成D还是等待接收下一位，如果下一位是0就可以解码成B，这就说明表中的编码不具有立刻可解码性

第二张表就具有立刻可解码性，因为任一字符的编码都不是另一个更长字符编码的前缀。只要收到的序列对应了某个字符的编码，直接解码成对应字符即可，无需等待后面的数据

我们的代码实现是用字符串构建哈夫曼树，只能针对由该字符串包含的字符组成的字符串进行编解码。代码里使用字符串存储的编码，实际上应该用bit进行存储

#include <iostream>
#include <string>
#include <vector>
#include <functional>
#include <unordered_map>
#include <queue>
using namespace std;
using uint = unsigned int;
class HuffmanTree {
public:
    // 这里的lambda表达式用来初始化function函数对象
    // priority_queue的构造函数指出，如果传入一个参数，那这个参数用来初始化比较器对象
    // 如果传入两个参数，第一个是比较器对象，第二个是底层容器
    HuffmanTree()
        :min_heap_([](Node* n1, Node* n2)->bool {return n1->weight_ > n2->weight_; })
        , root_(nullptr)
    {}
    ~HuffmanTree() {
        init();
        cout << "已释放所有内存！" << endl;
    }
    // 根据字符串创建哈夫曼树
    void create(const string& str) {
        if (root_ != nullptr) {
            cout << "哈夫曼树初始化..." << endl;
            init();
            cout << "初始化完成！" << endl;
        }
        // 统计频率（权重）
        unordered_map<char, uint> w_map;
        for (char c : str) {
            w_map[c]++;
        }
        // 遍历w_map，把所有的字符对应的权重放入小根堆，按照权重排序
        for (pair<const char, uint>& p : w_map) {
            min_heap_.push(new Node(p.first, p.second));
        }
        // 根据优先级队列，从小根堆中取出节点，构建哈夫曼树
        while (min_heap_.size() > 1) {
            Node* n1 = min_heap_.top();
            min_heap_.pop();
            Node* n2 = min_heap_.top();
            min_heap_.pop();
            Node* node = new Node('\0', n1->weight_ + n2->weight_);  // 内部节点存\0
            node->left_ = n1;
            node->right_ = n2;
            min_heap_.push(node);
        }
        root_ = min_heap_.top();
        min_heap_.pop();
        // 创建完哈夫曼树，直接对传入的海量字符进行编码并存储到code_map_
        create_huffman_code(str);
    }
    string get_code(const string& str) {
        // 利用哈夫曼树对str编码并返回
        string code;
        for (char c : str) {
            code += code_map_[c];
        }
        return code;
    }
    void show_huffman_code() const {
        // 打印哈夫曼编码
        for (const auto& pair : code_map_) {
            cout << pair.first << " : " << pair.second << endl;
        }
    }
    string decode(const string& encode_str) {
        Node* cur = root_;
        string decode_str;
        for (char c : encode_str) {
            if (c == '0') {
                cur = cur->left_;
            }
            else {
                cur = cur->right_;
            }
            if (cur->left_ == nullptr && cur->right_ == nullptr) {
                // 到达叶子节点
                decode_str.push_back(cur->data_);
                cur = root_;
            }
        }
        return decode_str;
    }
    uint get_wpl() {
        if (root_ == nullptr) {
            return 0;
        }
        if (root_->left_ == nullptr && root_->right_ == nullptr) {
            // 对于叶子节点，直接返回自己的weight * depth
            return root_->weight_ * 1;
        }
        else {
            // 对于内部节点，直接返回从子节点拿到的weight之和
            return get_w(root_->left_, 2) + get_w(root_->right_, 2);
        }
    }
private:
    struct Node {
        Node(char data, uint weight)
            :data_(data)
            , weight_(weight)
            , left_(nullptr)
            , right_(nullptr)
        {}
        char data_;
        uint weight_;
        Node* left_;
        Node* right_;
    };
private:
    // 防止当前对象重新构建哈夫曼树，释放所有的节点，然后初始化私有成员
    void init() {
        // 释放哈夫曼树的节点
        if (root_ != nullptr) {
            queue<Node*> q;
            q.push(root_);
            while (!q.empty()) {
                Node* node = q.front();
                q.pop();
                if (node->left_ != nullptr) {
                    q.push(node->left_);
                }
                if (node->right_ != nullptr) {
                    q.push(node->right_);
                }
                delete node;
            }
            MinHeap empty([](Node* n1, Node* n2)->bool {return n1->weight_ > n2->weight_; });
            swap(empty, min_heap_);
            code_map_.clear();
        }
    }
    void create_huffman_code(const string& str) {
        string code;
        create_huffman_code(root_, code);
    }
    void create_huffman_code(Node* node, string code) {
        if (node->left_ == nullptr && node->right_ == nullptr) {
            code_map_[node->data_] = code;
            return;
        }
        create_huffman_code(node->left_, code + "0");
        create_huffman_code(node->right_, code + "1");
    }
    uint get_w(Node* node, int depth) {
        if (node == nullptr) {
            return 0;
        }
        if (node->left_ == nullptr && node->right_ == nullptr) {
            // 对于叶子节点，直接返回自己的weight * depth
            return node->weight_ * depth;
        }
        else {
            // 对于内部节点，直接返回从子节点拿到的weight之和
            return get_w(node->left_, depth + 1) + get_w(node->right_, depth + 1);
        }
    }
private:
    Node* root_;
    unordered_map<char, string> code_map_;  // 存储字符对应的哈夫曼编码
    using MinHeap = priority_queue<Node*, vector<Node*>, function<bool(Node*, Node*)>>;
    MinHeap min_heap_; // 构建哈夫曼树的时候使用小根堆
};
int main() {
    string str = "Aa";
    HuffmanTree htree;
    htree.create(str);
    htree.show_huffman_code();
    cout << htree.get_wpl() << endl;
    str = "ABC";
    htree.create(str);
    htree.show_huffman_code();
    cout << htree.get_wpl() << endl;;
    string encode = htree.get_code(str);
    cout << "encode:" << encode << endl;
    cout << "decode:" << htree.decode(encode) << endl;
    return 0;
}

六、文件的压缩和解压缩

我们利用哈夫曼编码压缩文件的时候，如果文件是100M，我们可以压缩成20M，如果文件时1K，我们可能压缩成2K，当文件较小的时候，我们得到的压缩文件反而更大了，这是为什么？

文件的压缩过程如下：

• 按字节读取原文件的所有内容，并统计字节数据的权值，构建哈夫曼树
• 通过哈夫曼树，得到文件的哈夫曼编码
• 把文件的内容按字节进行编码，将编码内容按bit存储成压缩文件，还要存储文件字节数据以及权值

解码的过程如下：

• 读取原始文件的字节数据以及权值，构建哈夫曼树
• 读取压缩文件的01码，利用哈夫曼树对01进行解码，将解码数据存储成新的文件，就解码出了原始文件

由于压缩文件不仅存储01码，还需要存储文件字节数据以及权值用来重建哈夫曼树（就是代码中的w_map）。当原始文件较小时，文件字节数据以及权值可能大于原始文件的大小，故小文件压缩后可能变大

到此这篇关于C++详解哈夫曼树的概念与实现步骤的文章就介绍到这了,更多相关C++哈夫曼树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！