go语言编程学习实现图的广度与深度优先搜索

目录

• 图的实现
• BFS
• DFS

图的实现

所谓图就是节点及其连接关系的集合。所以可以通过一个一维数组表示节点，外加一个二维数组表示节点之间的关系。

//图的矩阵实现
typedef struct MGRAPH{
    nodes int[];    //节点
    edges int[][];  //边
}mGraph;

然而对于一些实际问题，其邻接矩阵中可能存在大量的0值，此时可以通过邻接链表来表示稀疏图，其数据结构如图所示

其左侧为图的示意图，右侧为图的邻接链表。红字表示节点序号，链表中为与这个节点相连的节点，如1节点与2、5节点相连。由于在go中，可以很方便地使用数组来代替链表，所以其链表结构可以写为

package main
import "fmt"
type Node struct{
	value int;      //节点为int型
};
type Graph struct{
	nodes []*Node
	edges map[Node][]*Node		//邻接表示的无向图
}

其中，map为Go语言中的键值索引类型，其定义格式为map[<op1>]<op2>，<op1>为键，<op2>为值。在图结构中，map[Node][]*Node表示一个Node对应一个Node指针所组成的数组。

下面将通过Go语言生成一个图

//增加节点
//可以理解为Graph的成员函数
func (g *Graph) AddNode(n *Node)  {
	g.nodes = append(g.nodes, n)
}
//增加边
func (g *Graph) AddEdge(u, v *Node) {
	g.edges[*u] = append(g.edges[*u],v)	//u->v边
	g.edges[*v] = append(g.edges[*v],u)	//u->v边
}
//打印图
func (g *Graph) Print(){
	//range遍历 g.nodes，返回索引和值
	for _,iNode:=range g.nodes{
		fmt.Printf("%v:",iNode.value)
		for _,next:=range g.edges[*iNode]{
			fmt.Printf("%v->",next.value)
		}
		fmt.Printf("\n")
	}
}
func initGraph() Graph{
	g := Graph{}
	for i:=1;i<=5;i++{
		g.AddNode(&Node{i,false})
	}
	//生成边
	A := [...]int{1,1,2,2,2,3,4}
	B := [...]int{2,5,3,4,5,4,5}
	g.edges = make(map[Node][]*Node)//初始化边
	for i:=0;i<7;i++{
		g.AddEdge(g.nodes[A[i]-1], g.nodes[B[i]-1])
	}
	return g
}
func main(){
	g := initGraph()
	g.Print()
}

其运行结果为

PS E:\Code> go run .\goGraph.go
1:2->5->
2:1->3->4->5->
3:2->4->
4:2->3->5->
5:1->2->4->

BFS

广度优先搜索(BFS)是最简单的图搜索算法，给定图的源节点后，向外部进行试探性地搜索。其特点是，通过与源节点的间隔来调控进度，即只有当距离源节点为 k k k的节点被搜索之后，才会继续搜索，得到距离源节点为 k + 1 k+1 k+1的节点。

对于图的搜索而言，可能存在重复的问题，即如果1搜索到2，相应地2又搜索到1，可能就会出现死循环。因此对于图中的节点，我们用searched对其进行标记，当其值为false时，说明没有被搜索过，否则则说明已经搜索过了。

type Node struct{
	value int;
	searched bool;
}
/*func initGraph() Graph{
    g := Graph{}
*/
    //相应地更改节点生成函数
    for i:=1;i<=5;i++{
		g.AddNode(&Node{i,false})
	}
/*
...
*/

此外，由于在搜索过程中会改变节点的属性，所以map所对应哈希值也会发生变化，即Node作为键值将无法对应原有的邻接节点，所以Graph中边的键值更替为节点的指针，这样即便节点的值发生变化，但其指针不会变化。

type Graph struct{
	nodes []*Node
	edges map[*Node][]*Node		//邻接表示的无向图
}
//增加边
func (g *Graph) AddEdge(u, v *Node) {
	g.edges[u] = append(g.edges[u],v)	//u->v边
	g.edges[v] = append(g.edges[v],u)	//u->v边
}
//打印图
func (g *Graph) Print(){
	//range遍历 g.nodes，返回索引和值
	for _,iNode:=range g.nodes{
		fmt.Printf("%v:",iNode.value)
		for _,next:=range g.edges[iNode]{
			fmt.Printf("%v->",next.value)
		}
		fmt.Printf("\n")
	}
}
func initGraph() Graph{
	g := Graph{}
	for i:=1;i<=9;i++{
		g.AddNode(&Node{i,false})
	}
	//生成边
	A := [...]int{1,1,2,2,2,3,4,5,5,6,1}
	B := [...]int{2,5,3,4,5,4,5,6,7,8,9}
	g.edges = make(map[*Node][]*Node)//初始化边
	for i:=0;i<11;i++{
		g.AddEdge(g.nodes[A[i]-1], g.nodes[B[i]-1])
	}
	return g
}
func (g *Graph) BFS(n *Node){
	var adNodes[] *Node		//存储待搜索节点
	n.searched = true
	fmt.Printf("%d:",n.value)
	for _,iNode:=range g.edges[n]{
		if !iNode.searched {
			adNodes = append(adNodes,iNode)
			iNode.searched=true
			fmt.Printf("%v ",iNode.value)
		}
	}
	fmt.Printf("\n")
	for _,iNode:=range adNodes{
		g.BFS(iNode)
	}
}
func main(){
	g := initGraph()
	g.Print()
	g.BFS(g.nodes[0])
}

该图为

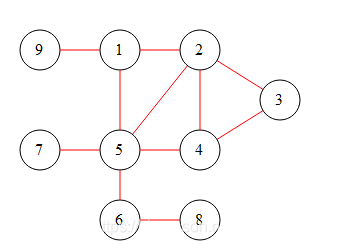
输出结果为

PS E:\Code\goStudy> go run .\goGraph.go
1:2->5->9->
2:1->3->4->5->
3:2->4->
4:2->3->5->
5:1->2->4->6->7->
6:5->8->
7:5->
8:6->
9:1->
//下面为BFS结果
1:2 5 9
2:3 4
3:
4:
5:6 7
6:8
8:
7:
9:

DFS

深度优先遍历(DFS)与BFS的区别在于，后者的搜索过程可以理解为逐层的，即可将我们初始搜索的节点看成父节点，那么与该节点相连接的便是一代节点，搜索完一代节点再搜索二代节点。DFS则是从父节点搜索开始，一直搜索到末代节点，从而得到一个末代节点的一条世系；然后再对所有节点进行遍历，找到另一条世系，直至不存在未搜索过的节点。

其基本步骤为：

• 首先选定一个未被访问过的顶点 V 0 V_0 V0​作为初始顶点，并将其标记为已访问
• 然后搜索 V 0 V_0 V0​邻接的所有顶点，判断是否被访问过，如果有未被访问的顶点，则任选一个顶点 V 1 V_1 V1​进行访问，依次类推，直到 V n V_n Vn​不存在未被访问过的节点为止。
• 若此时图中仍旧有顶点未被访问，则再选取其中一个顶点进行访问，否则遍历结束。

我们先实现第二步，即单个节点的最深搜索结果

func (g *Graph) visitNode(n *Node){
	for _,iNode:= range g.edges[n]{
		if !iNode.searched{
			iNode.searched = true
			fmt.Printf("%v->",iNode.value)
			g.visitNode(iNode)
			return
		}
	}
}
func main(){
	g := initGraph()
	g.nodes[0].searched = true
	fmt.Printf("%v->",g.nodes[0].value)
	g.visitNode(g.nodes[0])
}

结果为

PS E:\Code> go run .\goGraph.go
1->2->3->4->5->6->8->

即

可见，还有节点7、9未被访问。

完整的DFS算法只需在单点遍历之前，加上一个对所有节点的遍历即可

func (g *Graph) DFS(){
	for _,iNode:=range g.nodes{
		if !iNode.searched{
			iNode.searched = true
			fmt.Printf("%v->",iNode.value)
			g.visitNode(iNode)
			fmt.Printf("\n")
			g.DFS()
		}
	}
}
func main(){
	g := initGraph()
	g.nodes[0].searched = true
	fmt.Printf("%v->",g.nodes[0].value)
	g.visitNode(g.nodes[0])
}

结果为

PS E:\Code> go run .\goGraph.go
1->2->3->4->5->6->8->
7->
9->

以上就是go语言编程学习实现图的广度与深度优先搜索的详细内容，更多关于go语言实现图的广度与深度优先搜索的资料请关注我们其它相关文章！