彻底搞定堆排序:二叉堆

目录

• 二叉堆
• 插入
• 删除
• 构建
• 二叉堆代码实现
• 总结

二叉堆

什么是二叉堆

二叉堆本质上是一种完全二叉树，它分为两个类型

• 最大堆：最大堆的任何一个父节点的值，都大于等于它的左、右孩子节点的值（堆顶就是整个堆的最大元素）
• 最小堆：最小堆的任何一个父节点的值，都小于等于它的左、右孩子节点的值（堆顶就是整个堆的最小元素）

二叉堆的根节点叫做堆顶

二叉堆的基本操作

• 插入节点
• 删除节点
• 构建二叉堆

这几种操作都基于堆的自我调整，所谓堆自我调整，就是把一个不符合堆的完全二叉树，调整成一个堆，下面以最小堆为例。

插入

插入节点0的过程

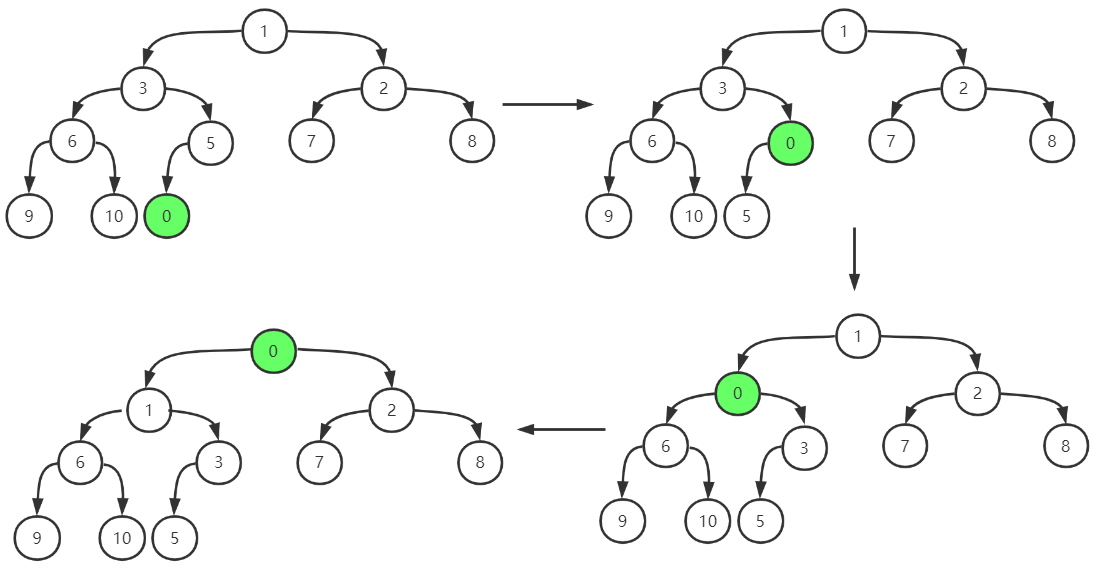
删除

删除节点的过程和插入的过程刚好相反，所删除的是处于堆顶的节点。例如删除1

• 为了维持完全二叉树的结构，把堆的最后一个元素临时补充到堆顶
• 删除原来10的位置
• 对堆顶的节点10执行下沉操作

构建

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质就是让所有的非叶子节点一次下沉

二叉堆代码实现

二查堆虽然是一颗完全二叉树，但它的存储方式并不是链式的，而是顺序存储，换句话说，二叉堆的所有节点都存储在数组中

当父节点为parent时，左孩子为2 * parent + 1；右孩子为2 * parent + 2

/**
 * @author ：zsy
 * @date ：Created 2021/5/17 9:41
 * @description：二叉堆
 */
public class HeapTest {
    public static void main(String[] args) {
        int[] arr = {1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
        Heap heap = new Heap(arr);
        heap.upAdjust(arr);
        System.out.println(Arrays.toString(arr));
        arr = new int[]{7, 1, 3, 10, 5, 2, 8, 9, 6};
        heap = new Heap(arr);
        heap.buildHead();
        System.out.println(Arrays.toString(arr));
    }
}
class Heap {
    private int[] arr;
    public Heap(int[] arr) {
        this.arr = arr;
    }
    public void buildHead() {
        //从最后一个非叶子节点开始，依次下沉
        for (int i = (arr.length - 2) / 2; i >= 0; i--) {
            downAdjust(arr, i, arr.length);
        }
    }
    private void downAdjust(int[] arr, int parentIndex, int length) {
        int temp = arr[parentIndex];
        int childrenIndex = parentIndex * 2 + 1;
        while (childrenIndex < length) {
            //如果有右孩子，并且右孩子小于左孩子，那么定位到右孩子
            if (childrenIndex + 1 < length && arr[childrenIndex + 1] < arr[childrenIndex]) {
                childrenIndex++;
            }
            //如果父节点小于较小孩子节点的值，直接跳出
            if (temp <= arr[childrenIndex]) break;
            //无需交换，单向赋值
            arr[parentIndex] = arr[childrenIndex];
            parentIndex = childrenIndex;
            childrenIndex = 2 * childrenIndex + 1;
        }
        arr[parentIndex] = temp;
    }
    public void upAdjust(int[] arr) {
        int childrenIndex = arr.length - 1;
        int parentIndex = (childrenIndex - 1) / 2;
        int temp = arr[childrenIndex];
        while (childrenIndex > 0 && temp < arr[parentIndex]) {
            //单向赋值
            arr[childrenIndex] = arr[parentIndex];
            childrenIndex = parentIndex;
            parentIndex = (parentIndex - 1) / 2;
        }
        arr[childrenIndex] = temp;
    }
}

结果：

[0, 1, 2, 6, 3, 7, 8, 9, 10, 5]
[1, 5, 2, 6, 7, 3, 8, 9, 10]

总结

本篇文章就到这里了，希望能给你带来帮助，也希望您能够多多关注我们的更多内容！