Python numpy.transpose使用详解

前言

看Python代码时，碰见 numpy.transpose 用于高维数组时挺让人费解，通过一番画图分析和代码验证，发现 transpose 用法还是很简单的。

注：评论中说的三维坐标图中的 0 1 2 3 标反了，已经修正，感谢大家提醒（2019.02）。

正文

Numpy 文档 numpy.transpose中做了些解释，transpose 作用是改变序列，下面是一些文档Examples：

代码1：

x = np.arange(4).reshape((2,2))

输出1：

#x 为：
array([[0, 1],
       [2, 3]])

代码2：

import numpy as np
x.transpose()

输出2：

array([[0, 2],
       [1, 3]])

对于二维 ndarray，transpose在不指定参数是默认是矩阵转置。如果指定参数，有如下相应结果：

代码3：

x.transpose((0,1))

输出3：

# x 没有变化
array([[0, 1],
       [2, 3]])

代码4：

x.transpose((1,0))

输出4：

# x 转置了
array([[0, 2],
       [1, 3]])

这个很好理解：
对于x，因为：

代码5：

x[0][0] == 0
x[0][1] == 1
x[1][0] == 2
x[1][1] == 3

我们不妨设第一个方括号“[]”为 0轴 ，第二个方括号为 1轴 ，则x可在 0-1坐标系 下表示如下：

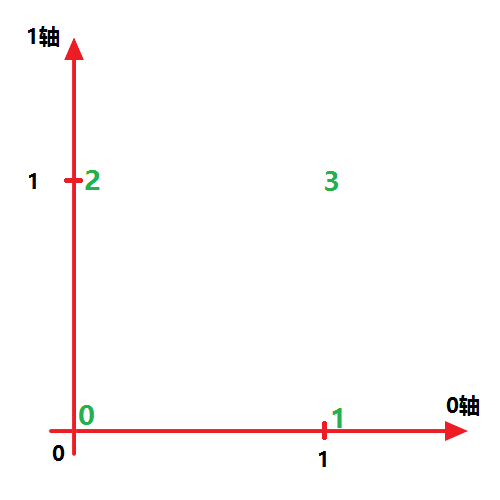
代码6：

因为 x.transpose((0,1)) 表示按照原坐标轴改变序列，也就是保持不变
而 x.transpose((1,0)) 表示交换 ‘0轴’ 和 ‘1轴’，所以就得到如下图所示结果：

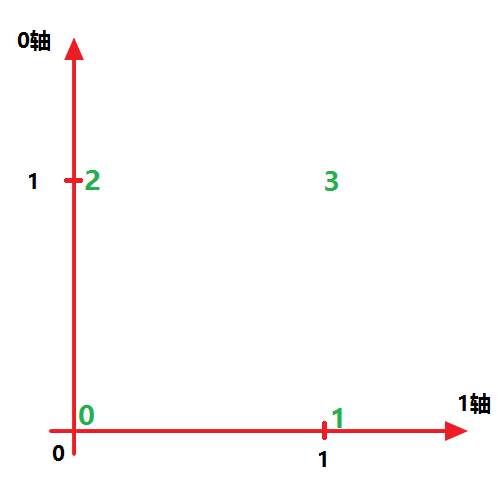
注意，任何时候你都要保持清醒，告诉自己第一个方括号“[]”为 0轴 ，第二个方括号为 1轴
此时，transpose转换关系就清晰了。

我们来看一个三维的：

代码7：

import numpy as np

# A是array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15])
A = np.arange(16)

# 将A变换为三维矩阵
A = A.reshape(2,2,4)
print(A)

输出7：

A = array([[[ 0,  1,  2,  3],
            [ 4,  5,  6,  7]],
            
           [[ 8,  9, 10, 11],
            [12, 13, 14, 15]]])

我们对上述的A表示成如下三维坐标的形式：

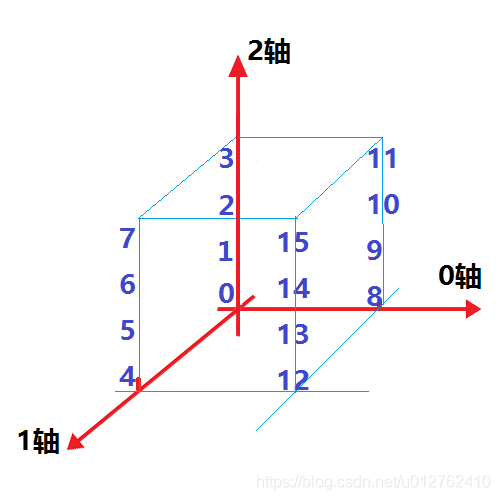
所以对于如下的变换都很好理解啦：

代码8：

A.transpose((0,1,2))  #保持A不变
A.transpose((1,0,2))  #将 0轴 和 1轴 交换

将 0轴 和 1轴 交换：

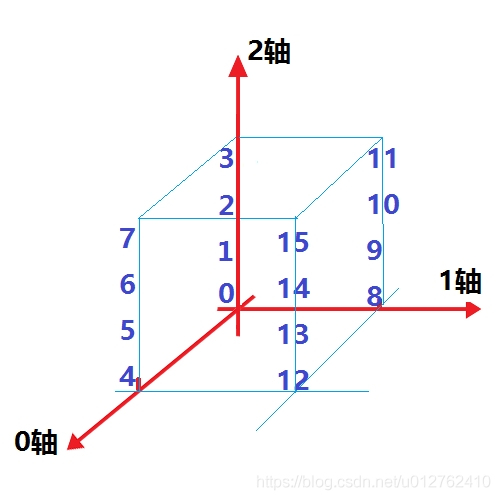
此时，输出

代码9：

A.transpose((1,0,2)) [0][1][2]	#根据上图这个结果应该是10

后面不同的参数以此类推。

到此这篇关于Python numpy.transpose使用详解的文章就介绍到这了,更多相关Python numpy.transpose内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • numpy.transpose()实现数组的转置例子

    说到转置操作,顺便提及矩阵与数组的区别: 矩阵:数学里的概念,其元素只能是数值,这也是区别于数组的根本所在 数组:计算机中的概念,代表一种数据组织.存储方式,其元素可以是数字.也可以是字符 数组的转置操作,是借鉴了线性代数中矩阵的转置操作.将行与列对调,即第一行变成第一列-..或第一列变成第一行-..的操作即使转置操作. 1. 多维数组的转置 import numpy as np test = np.array([[12,4,7,0],[3,7,45,81]]) test # 以下为test输出

  • 详解Numpy数组转置的三种方法T、transpose、swapaxes

    Numpy是高性能科学计算和数据分析的基础包,里面包含了许多对数组进行快速运算的标准数学函数,掌握这些方法,能摆脱数据处理时的循环. 1.首先数组转置(T) 创建二维数组data如下: 进行矩阵运算时,经常要用数组转置,比如计算矩阵内积X^T X.这时就需要利用数组转置,如下: 2.轴对换之transpose 对于高维数组,可以使用轴对换来对多个维度进行变换. 这里创建了一个三维数组,各维度大小分别为2,3,4. transpose进行的操作其实是将各个维度重置,原来(2,3,4)对应的是(0,

  • numpy.transpose对三维数组的转置方法

    如下所示: import numpy as np 三维数组 arr1 = np.arange(16).reshape((2, 2, 4)) #[[[ 0 1 2 3] # [ 4 5 6 7]] # [[ 8 9 10 11] # [12 13 14 15]]] arr2=arr1.transpose((1,0,2)) #[[[ 0 1 2 3] # [ 8 9 10 11]] # # [[ 4 5 6 7] # [12 13 14 15]]] 正序为(0,1,2),数组为 #[[[ 0 1 2

  • Numpy中转置transpose、T和swapaxes的实例讲解

    利用Python进行数据分析时,Numpy是最常用的库,经常用来对数组.矩阵等进行转置等,有时候用来做数据的存储. 在numpy中,转置transpose和轴对换是很基本的操作,下面分别详细讲述一下,以免自己忘记. In [1]: import numpy as np In [2]: arr=np.arange(16).reshape(2,2,4) In [3]: arr Out[3]: array([[[ 0, 1, 2, 3], [ 4, 5, 6, 7]], [[ 8, 9, 10, 11

  • 对numpy中的transpose和swapaxes函数详解

    transpose() 这个函数如果括号内不带参数,就相当于转置,和.T效果一样,而今天主要来讲解其带参数. 我们看如下一个numpy的数组: `arr=np.arange(16).reshape((2,2,4)) arr= array([[[ 0, 1, 2, 3], [ 4, 5, 6, 7]], [[ 8, 9, 10, 11], [12, 13, 14, 15]]]) ` 那么有: arr.transpose(2,1,0) array([[[ 0, 8], [ 4, 12]], [[ 1

  • 对numpy下的轴交换transpose和swapaxes的示例解读

    如下所示: 解读: transpose( ) 方法的参数是一个 由 轴编号(轴编号自0 开始) 序列构成的 元组. 开始时,数组的轴编号序列是默认从 0开始的 :0,1,2,, 坐标的顺序也是这个轴编号的顺序,(0,1,2) 当使用 transpose 时候,轴编号的顺序变成了 (1,0,2) 说明 0号轴和1号轴的顺序变了, 那么,坐标的顺序也应该变了, 例如 元素 8: 开始时:根据轴顺序 0,1,2.他的坐标是 (1,0,0) 现在,根据周顺序 1,0,2:他的坐标是(0,1,0). sw

  • Python numpy.transpose使用详解

    Python numpy.transpose使用详解

    前言 看Python代码时,碰见 numpy.transpose 用于高维数组时挺让人费解,通过一番画图分析和代码验证,发现 transpose 用法还是很简单的. 注:评论中说的三维坐标图中的 0 1 2 3 标反了,已经修正,感谢大家提醒(2019.02). 正文 Numpy 文档 numpy.transpose中做了些解释,transpose 作用是改变序列,下面是一些文档Examples: 代码1: x = np.arange(4).reshape((2,2)) 输出1: #x 为:ar

  • Python NumPy矩阵对象详解及方法

    目录 1. 介绍 2. 创建矩阵 3. 矩阵特有属性 4. 矩阵乘法 1. 介绍 在数学上,矩阵(Matrix)是一个按照矩形阵列排列的负数或实数集合,但在NumPy中,矩阵np.matrix是数组np.ndarray的派生类.这意味着矩阵本质上是   一个数组,拥有数组的所有属性和方法:同时,矩阵又有一些不同于数组的特性和方法首先,矩阵是二维的,不能像数组一样幻化成任意维度,即使展开或切片,返回也是二维的:其次,矩阵和矩阵.矩阵和数组都可以做加减乘除运算,运算结果都是返回矩阵:最后,矩阵的乘法

  • Python常用库Numpy进行矩阵运算详解

    Numpy支持大量的维度数组和矩阵运算,对数组运算提供了大量的数学函数库! Numpy比Python列表更具优势,其中一个优势便是速度.在对大型数组执行操作时,Numpy的速度比Python列表的速度快了好几百.因为Numpy数组本身能节省内存,并且Numpy在执行算术.统计和线性代数运算时采用了优化算法. Numpy的另一个强大功能是具有可以表示向量和矩阵的多维数组数据结构.Numpy对矩阵运算进行了优化,使我们能够高效地执行线性代数运算,使其非常适合解决机器学习问题. 与Python列表相比

  • Python中Numpy模块使用详解

    Python中Numpy模块使用详解

    目录 NumPy ndarray对象 ​ ​Numpy数据类型​​ Numpy数组属性 NumPy NumPy(Numerical Python) 是 Python 的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库.Nupmy可用来存储和处理大型矩阵,比Python自身的嵌套列表(nested list structure)结构要高效的多(该结构也可以用来表示矩阵(matrix)).据说NumPy将Python相当于变成一种免费的更强大的MatLab系统.

  • python目标检测yolo2详解及预测代码复现

    python目标检测yolo2详解及预测代码复现

    目录 前言 实现思路 1.yolo2的预测思路(网络构建思路) 2.先验框的生成 3.利用先验框对网络的输出进行解码 4.进行得分排序与非极大抑制筛选 实现结果 前言 ……最近在学习yolo1.yolo2和yolo3,写这篇博客主要是为了让自己对yolo2的结构有更加深刻的理解,同时要理解清楚先验框的含义. 尽量配合代码观看会更容易理解. 直接下载 实现思路 1.yolo2的预测思路(网络构建思路) YOLOv2使用了一个新的分类网络DarkNet19作为特征提取部分,DarkNet19包含19

  • Python内置模块turtle绘图详解

    Python内置模块turtle绘图详解

    urtle库是Python语言中一个很流行的绘制图像的函数库,想象一个小乌龟,在一个横轴为x.纵轴为y的坐标系原点,(0,0)位置开始,它根据一组函数指令的控制,在这个平面坐标系中移动,从而在它爬行的路径上绘制了图形. turtle绘图的基础知识: 1.画布(canvas) 画布就是turtle为我们展开用于绘图区域,我们可以设置它的大小和初始位置. 设置画布大小 turtle.screensize(canvwidth=None,canvheight=None,bg=None),参数分别为画布的

  • Python pandas常用函数详解

    本文研究的主要是pandas常用函数,具体介绍如下. 1 import语句 import pandas as pd import numpy as np import matplotlib.pyplot as plt import datetime import re 2 文件读取 df = pd.read_csv(path='file.csv') 参数:header=None 用默认列名,0,1,2,3... names=['A', 'B', 'C'...] 自定义列名 index_col='

  • opencv3/Python 稠密光流calcOpticalFlowFarneback详解

    光流是由物体或相机的运动引起的图像对象在两个连续帧之间的视在运动模式.光流方法计算在t和 t+Δtt+Δt时刻拍摄的两个图像帧之间的每个像素的运动位置.这些方法被称为差分,因为它们基于图像信号的局部泰勒级数近似; 也就是说,它们使用关于空间和时间坐标的偏导数. 和稀疏光流相比,稠密光流不仅仅是选取图像中的某些特征点(一般用角点)进行计算;而是对图像进行逐点匹配,计算所有点的偏移量,得到光流场,从而进行配准.因此其计算量会显著大于稀疏光流,但效果一般优于稀疏光流. 函数: def calcOpti

  • opencv python图像梯度实例详解

    这篇文章主要介绍了opencv python图像梯度实例详解,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下 一阶导数与Soble算子 二阶导数与拉普拉斯算子 图像边缘: Soble算子: 二阶导数: 拉普拉斯算子: import cv2 as cv import numpy as np # 图像梯度(由x,y方向上的偏导数和偏移构成),有一阶导数(sobel算子)和二阶导数(Laplace算子) # 用于求解图像边缘,一阶的极大值,二阶的零点

  • Python插件机制实现详解

    插件机制是代码/功能反向依赖注入到主体程序的一种方法,编译型语言通过动态加载动态库实现插件.对于Python这样的脚本语言,实现插件机制更简单. 机制 Python的__import__方法可以动态地加载Python文件,即以某个py脚本的文件名作为__import__的参数,在程序运行的时候加载py脚本程序模块.对应的import关键字则是静态加载依赖的py模块. 描述 __import__() 函数用于动态加载类和函数 . 如果一个模块经常变化就可以使用 __import__() 来动态载入

随机推荐