Spark GraphX 分布式图处理框架图算法详解

目录

• 正文
• Graphx图结构
• 1. 最短路径
• 示例数据
• 可视化数据
• 计算最短路径
• 2. 网页排名
• 数据可视化
• pagerank算法测试
• 算法结果
• 3. 连通域（连通组件）
• 加载图测试连通域
• 生成图测试
• 图实例的形态展示
• 强连接域的计算
• 4. 三角计数
• 代码测试
• 测试结果
• 5. 标签传播算法（LPA）
• 基本思想

正文

Spark GraphX是一个分布式图处理框架，基于 Pregel 接口实现了常用的图算法。

包括 PageRank、SVDPlusPlus、TriangleCount、 ConnectedComponents、LPA 等算法，以下通过具象化的图实例理解相应的算法用途。

Graphx图结构

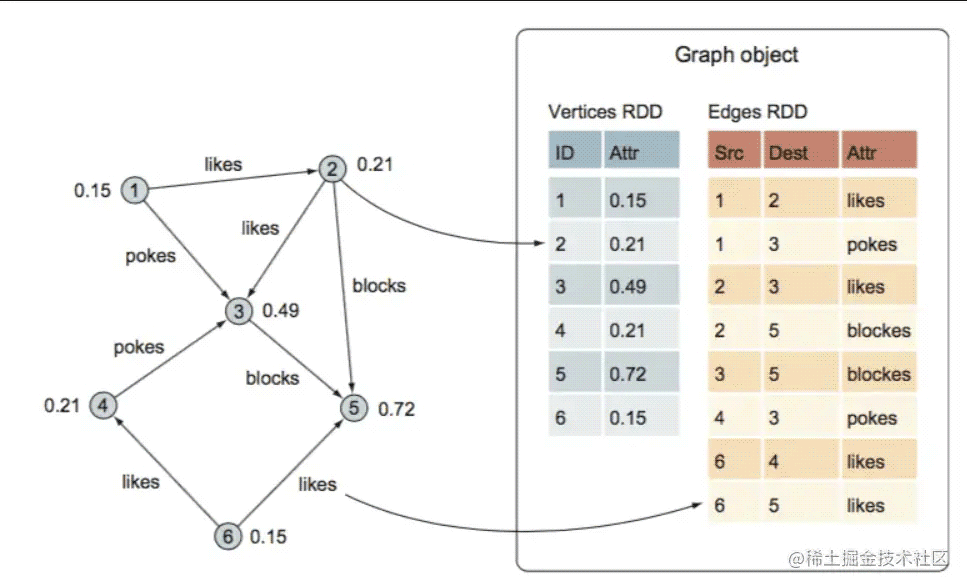
Graphx中的Graph有两个RDD，一个是边RDD，一个是点RDD。

此外，三元组其实就是（点、边，点）一个有效组合，由triplets()接口获取，triplets()返回的结果是EdgeTriplet[VD,ED]。

1. 最短路径

最常见的路径搜索算法（例如DFS & BFS、最短路径、 最小生成树、随机游走等），最短路径是最容易理解的图算法，因为大家在生活中能够广泛接触到，如驾驶导航，外卖送餐路线等等。

路径搜索算法建立在图搜索算法的基础上，用来探索节点之间的路径。这些路径从一个节点开始，遍历关系，直到到达目的地，Graphx采用了最短路径算法Dijkstra的原理。

示例数据

// 输入一些边数据
val edgeSeq: Seq[(Int, Int)] = Seq((1, 2), (1, 5), (2, 3), (2, 5), (3, 4), (4, 5), (4, 6),(6, 9),(9, 11)).flatMap(e => Seq(e, e.swap))
val edges = op.sc.parallelize(edgeSeq).map { case (v1, v2) => (v1.toLong, v2.toLong) }

可视化数据

这是上述数据的图形表示（双向边，无权）

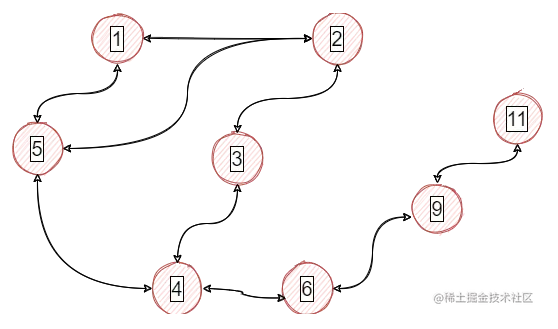
计算最短路径

val graph_sp = Graph.fromEdgeTuples(edges, 1)
val landmarks = Seq(1, 11).map(_.toLong)
val results = ShortestPaths.run(graph_sp, landmarks).vertices.collect.map {
  case (v, spMap) => (v, spMap.mapValues(i => i))
}

全部结果打印：

println(results.mkString)
(1,Map(1 -> 0, 11 -> 5))
(2,Map(1 -> 1, 11 -> 5))
(3,Map(1 -> 2, 11 -> 4))
(4,Map(1 -> 2, 11 -> 3))
(5,Map(1 -> 1, 11 -> 4))
(6,Map(11 -> 2, 1 -> 3))
(9,Map(11 -> 1, 1 -> 4))
(11,Map(11 -> 0, 1 -> 5))

上述计算了图中所有点到点1和点11的最短距离，（起点id，Map（目标1 -> 最短路径长度，目标2 -> 最短路径长度））。例如5,Map(1 -> 1, 11 -> 4)说明从5到1最短距离是1，5到11的最短距离是4。

2. 网页排名

PageRank度量一个图中每个顶点的重要程度，假定从u到v的一条边代表v的重要性标签。例如，一个微博用户被许多其它人粉，该用户排名很高。GraphX带有静态和动态PageRank的实现方法，这些方法在PageRank object中。静态的PageRank运行固定次数的迭代，而动态的PageRank一直运行，直到收敛。

GraphX有一个我们可以运行PageRank的社交网络数据集的简单数据。用户集在graphx/data/users.txt中，用户之间的关系在graphx/data/followers.txt中（Spark的源码或编译后文件里都包含）。

数据可视化

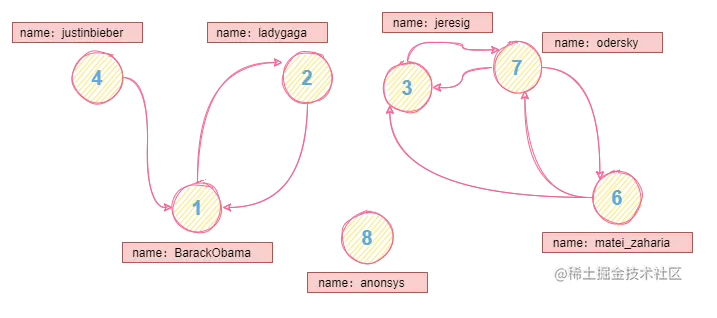
pagerank算法测试

先说PageRank动态实现，以下调用就是动态的，实际是调用runUntilConvergence()不能指定迭代次数。参数0.0001是个容忍度，是在对图进行迭代过程中退出迭代的条件，而静态的PageRank不可传递该参数，但可以指定迭代次数【固定次数，所以静态】。

val graph: Graph[Int, Int] = GraphLoader
      .edgeListFile(op.sc, "followers.txt", canonicalOrientation = true, numEdgePartitions = 1)
val ranks = graph.pageRank(0.0001).vertices.sortBy(_._2, ascending = false)
ranks.take(5).foreach(println(_))

算法结果

(7,1.8138212152810693)
(2,1.0692956678358136)
(4,0.8759124087591241)
(6,0.8759124087591241)
(1,0.6825291496824343)
# join name
(odersky,1.8138212152810693)
(ladygaga,1.0692956678358136)
(justinbieber,0.8759124087591241)
(matei_zaharia,0.8759124087591241)
(BarackObama,0.6825291496824343)

二元组左侧是顶点信息，右侧是重要程度，也就是分数越高排名越靠前。

这个结果有一些顺序跟直观感受不符，点7最重要毋庸置疑，点1的重要性应该是大于点4的，但是结果不是这样，那么数据集大一些会更好吗？？

personalizedPageRank()方法还可以进行个性化推荐，比如社交网络中，给某用户再推荐一个人，或者对于用户商品的推荐中，用户商品两个实体可以形成一个图，我们就可以根据具体的某个用户来给他推荐一些商品。

3. 连通域（连通组件）

连通分量算法用其编号最小的顶点的 ID 标记图中的每个连通分量。例如，在社交网络中，连接的组件可以近似集群。

加载图测试连通域

这里的graph仍然是加载followers.txt数据，spark自带的有。

val cc: Graph[VertexId, Int] = graph.connectedComponents()
println("连通结果展示++++++++：")
cc.vertices.map(_.swap)
  .groupByKey()
  .map(_._2)
  .foreach(println)

结果展示（跟图形观察的结果是一致）：

连通结果展示++++++++：
CompactBuffer(4, 1, 2)
CompactBuffer(6, 3, 7)

可以看到是2个域。结果图数据本身不是这样组织的，为了便于理解进行了聚合。原始数据collect回来是这样：

Array((4,1), (1,1), (6,3), (3,3), (7,3), (2,1))

元组左侧是顶点，右侧表示归属，这个结果符合预期。

生成图测试

val g = Graph(sc.makeRDD((1L to 7L).map((_,""))),
      sc.makeRDD(Array(Edge(2L,5L,""), Edge(5L,3L,""), Edge(3L,2L,""),
        Edge(4L,5L,""), Edge(6L,7L,""))))
    g.connectedComponents
      .vertices
      .map(_.swap)
      .groupByKey()
      .map(_._2)
      .foreach(println)

图实例的形态展示

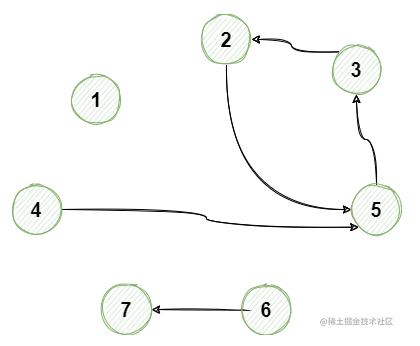
这样的代码便于自行组织一套图数据，按自己意思进行修改，运行上述代码得到结果是：

CompactBuffer(1)
CompactBuffer(2, 3, 4, 5)
CompactBuffer(6, 7)

强连接网络就是：在这个网络中无论你从哪个顶点开始，其他所有顶点都是可达的。

强连接域的计算

g.stronglyConnectedComponents(3)
      .vertices.map(_.swap)
      .groupByKey()
      .map(_._2)
      .filter(_.size > 1)
      .foreach(println)

过滤掉那些单点的域，那么强连接的计算结果是CompactBuffer(2, 3, 5)。

4. 三角计数

当一个顶点有两个相邻的顶点并且它们之间有一条边时，它就是三角形的一部分。需要注意的是，在计算社交网络数据集的三角形计数时，TriangleCount需要边的方向是规范的方向(srcId < dstId),并且图通过Graph.partitionBy分片过。

三角计数统计应用场景：大规模的社区发现，通过该算法可以做群体检测。只要是跟大规模小团体检测方面该算法都可以很好的支持，算法是找出拥有三角形环关系的最多的顶点。

Triangle Count的算法思想如下：

• 计算每个结点的邻结点；
• 对通过每条边的两个顶点相联的顶点的相邻点集合计算交集，并找出交集中id大于前两个结点id的结点；
• 对每个结点统计Triangle总数，注意只统计符合计算方向的Triangle Count。

代码测试

val graph2 = graph.partitionBy(PartitionStrategy.RandomVertexCut)
// Find the triangle count for each vertex
val triCounts = graph2.triangleCount().vertices
println(triCounts.collect().mkString("\n"))

开头先对图graph进行了分片得到graph2。

测试结果

这个意思是6，3，7顶点分别拥有1个三角环，而其他顶点没有，实际上正是6，3，7组成了三角。

(4,0)
(1,0)
(6,1)
(3,1)
(7,1)
(2,0)

5. 标签传播算法（LPA）

Label Propagation，是一种基于图的半监督学习算法(Semi-supervised learning)，应用场景为：社区发现(Community detection)。社区发现的过程就是一种聚类的过程。主要是用于团体检测，LPA能够以接近线性复杂度去检测一个大规模图中的团体结构，主要思想是给所有顶点中的密集连接组打上一个唯一标签，这些拥有相同标签的组就是所谓的团体。

它不保证收敛，且迭代次数足够多之后，所有联通节点最终收敛为一个社区。

该算法也可以用于半监督学习（大部分没有标签，小部分有标签），给那些没有标签的通过标签传播算法进行打标签。也可以应用于风控，对于通过已有风险评估的人，通过社交网络去评估跟其有关系的人的风险。

基本思想

标签传播算法的应用场景是不重叠社区发现，其基本思想是：将一个节点的邻居节点的标签中数量最多的标签作为该节点自身的标签。给每个节点添加标签（label）以代表它所属的社区，并通过标签的“传播”形成同一标签的“社区”结构。简而言之，你的邻居属于哪个label最多，你就属于哪个label。该算法的有点是收敛周期短，除了迭代次数无需任何先验参数(不需事先指定社区个数和大小)，算法执行过程中不需要计算任何社区指标。

以上就是Spark GraphX 分布式图处理框架图算法详解的详细内容，更多关于Spark GraphX 图算法的资料请关注我们其它相关文章！