python机器学习理论与实战（五）支持向量机

做机器学习的一定对支持向量机（support vector machine-SVM）颇为熟悉，因为在深度学习出现之前，SVM一直霸占着机器学习老大哥的位子。他的理论很优美，各种变种改进版本也很多，比如latent-SVM, structural-SVM等。这节先来看看SVM的理论吧，在（图一）中A图表示有两类的数据集，图B,C,D都提供了一个线性分类器来对数据进行分类？但是哪个效果好一些？

（图一）

可能对这个数据集来说，三个的分类器都一样足够好了吧，但是其实不然，这个只是训练集，现实测试的样本分布可能会比较散一些，各种可能都有，为了应对这种情况，我们要做的就是尽可能的使得线性分类器离两个数据集都尽可能的远，因为这样就会减少现实测试样本越过分类器的风险，提高检测精度。这种使得数据集到分类器之间的间距（margin）最大化的思想就是支持向量机的核心思想，而离分类器距离最近的样本成为支持向量。既然知道了我们的目标就是为了寻找最大边距，怎么寻找支持向量？如何实现？下面以（图二）来说明如何完成这些工作。

（图二）

假设（图二）中的直线表示一个超面，为了方面观看显示成一维直线，特征都是超面维度加一维度的，图中也可以看出，特征是二维，而分类器是一维的。如果特征是三维的，分类器就是一个平面。假设超面的解析式为，那么点A到超面的距离为,下面给出这个距离证明：

（图三）

在（图三）中，青色菱形表示超面，Xn为数据集中一点，W是超面权重，而且W是垂直于超面的。证明垂直很简单，假设X'和X''都是超面上的一点，

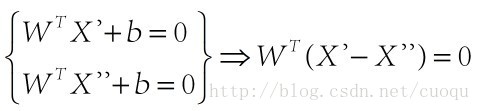
因此W垂直于超面。知道了W垂直于超面，那么Xn到超面的距离其实就是Xn和超面上任意一点x的连线在W上的投影，如（图四）所示：

套进拉格朗日乘子法公式得到如（公式五）所示的样子：

（公式五）

在（公式五）中通过拉格朗日乘子法函数分别对W和b求导，为了得到极值点，令导数为0，得到

,然后把他们代入拉格朗日乘子法公式里得到（公式六）的形式：

（公式六）

（公式六）后两行是目前我们要求解的优化函数，现在只需要做个二次规划即可求出alpha,二次规划优化求解如（公式七）所示：

（公式七）

通过（公式七）求出alpha后，就可以用（公式六）中的第一行求出W。到此为止，SVM的公式推导基本完成了，可以看出数学理论很严密，很优美，尽管有些同行们认为看起枯燥，但是最好沉下心来从头看完，也不难，难的是优化。二次规划求解计算量很大，在实际应用中常用SMO（Sequential minimal optimization）算法，SMO算法打算放在下节结合代码来说。

参考文献：

[1]machine learning in action. Peter Harrington

[2] Learning From Data. Yaser S.Abu-Mostafa

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python中使用支持向量机(SVM)算法

    Python中使用支持向量机(SVM)算法

    在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别.分类(异常值检测)以及回归分析. 其具有以下特征: (1)SVM可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值.而其他分类方法都采用一种基于贪心学习的策略来搜索假设空间,这种方法一般只能获得局部最优解.   (2) SVM通过最大化决策边界的边缘来实现控制模型的能力.尽管如此,用户必须提供其他参数,如使用核函数类型和引入松弛变量等.   (3)S

  • Python SVM(支持向量机)实现方法完整示例

    Python SVM(支持向量机)实现方法完整示例

    本文实例讲述了Python SVM(支持向量机)实现方法.分享给大家供大家参考,具体如下: 运行环境 Pyhton3 numpy(科学计算包) matplotlib(画图所需,不画图可不必) 计算过程 st=>start: 开始 e=>end: 结束 op1=>operation: 读入数据 op2=>operation: 格式化数据 cond=>condition: 是否达到迭代次数 op3=>operation: 寻找超平面分割最小间隔 ccond=>cond

  • Python中使用支持向量机SVM实践

    在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别.分类(异常值检测)以及回归分析. 其具有以下特征: (1)SVM可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值.而其他分类方法都采用一种基于贪心学习的策略来搜索假设空间,这种方法一般只能获得局部最优解. (2) SVM通过最大化决策边界的边缘来实现控制模型的能力.尽管如此,用户必须提供其他参数,如使用核函数类型和引入松弛变量等. (3)SVM一般

  • SVM基本概念及Python实现代码

    SVM基本概念及Python实现代码

    SVM(support vector machine)支持向量机: 注意:本文不准备提到数学证明的过程,一是因为有一篇非常好的文章解释的非常好:支持向量机通俗导论(理解SVM的三层境界),另一方面是因为我只是个程序员,不是搞数学的(主要是因为数学不好.),主要目的是将SVM以最通俗易懂,简单粗暴的方式解释清楚. 线性分类: 先从线性可分的数据讲起,如果需要分类的数据都是线性可分的,那么只需要一根直线f(x)=wx+b就可以分开了,类似这样: 这种方法被称为:线性分类器,一个线性分类器的学习目标便

  • Python中支持向量机SVM的使用方法详解

    除了在Matlab中使用PRTools工具箱中的svm算法,Python中一样可以使用支持向量机做分类.因为Python中的sklearn库也集成了SVM算法,本文的运行环境是Pycharm. 一.导入sklearn算法包 Scikit-Learn库已经实现了所有基本机器学习的算法,具体使用详见官方文档说明 skleran中集成了许多算法,其导入包的方式如下所示, 逻辑回归:from sklearn.linear_model import LogisticRegression 朴素贝叶斯:fro

  • 手把手教你python实现SVM算法

    手把手教你python实现SVM算法

    什么是机器学习 (Machine Learning) 机器学习是研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能.它是人工智能的核心,是使计算机具有智能的根本途径,其应用遍及人工智能的各个领域. 机器学习的大致分类: 1)分类(模式识别):要求系统依据已知的分类知识对输入的未知模式(该模式的描述)作分析,以确定输入模式的类属,例如手写识别(识别是不是这个数). 2)问题求解:要求对于给定的目标状态,寻找一个将当前状态转换为目标状态的动作序

  • python实现基于SVM手写数字识别功能

    python实现基于SVM手写数字识别功能

    本文实例为大家分享了SVM手写数字识别功能的具体代码,供大家参考,具体内容如下 1.SVM手写数字识别 识别步骤: (1)样本图像的准备. (2)图像尺寸标准化:将图像大小都标准化为8*8大小. (3)读取未知样本图像,提取图像特征,生成图像特征组. (4)将未知测试样本图像特征组送入SVM进行测试,将测试的结果输出. 识别代码: #!/usr/bin/env python import numpy as np import mlpy import cv2 print 'loading ...'

  • Python机器学习之SVM支持向量机

    Python机器学习之SVM支持向量机

    SVM支持向量机是建立于统计学习理论上的一种分类算法,适合与处理具备高维特征的数据集. SVM算法的数学原理相对比较复杂,好在由于SVM算法的研究与应用如此火爆,CSDN博客里也有大量的好文章对此进行分析,下面给出几个本人认为讲解的相当不错的: 支持向量机通俗导论(理解SVM的3层境界) JULY大牛讲的是如此详细,由浅入深层层推进,以至于关于SVM的原理,我一个字都不想写了..强烈推荐. 还有一个比较通俗的简单版本的:手把手教你实现SVM算法 SVN原理比较复杂,但是思想很简单,一句话概括,就

  • python机器学习理论与实战（六）支持向量机

    python机器学习理论与实战（六）支持向量机

    上节基本完成了SVM的理论推倒,寻找最大化间隔的目标最终转换成求解拉格朗日乘子变量alpha的求解问题,求出了alpha即可求解出SVM的权重W,有了权重也就有了最大间隔距离,但是其实上节我们有个假设:就是训练集是线性可分的,这样求出的alpha在[0,infinite].但是如果数据不是线性可分的呢?此时我们就要允许部分的样本可以越过分类器,这样优化的目标函数就可以不变,只要引入松弛变量即可,它表示错分类样本点的代价,分类正确时它等于0,当分类错误时,其中Tn表示样本的真实标签-1或者1,回顾

  • python机器学习理论与实战（五）支持向量机

    做机器学习的一定对支持向量机(support vector machine-SVM)颇为熟悉,因为在深度学习出现之前,SVM一直霸占着机器学习老大哥的位子.他的理论很优美,各种变种改进版本也很多,比如latent-SVM, structural-SVM等.这节先来看看SVM的理论吧,在(图一)中A图表示有两类的数据集,图B,C,D都提供了一个线性分类器来对数据进行分类?但是哪个效果好一些? (图一) 可能对这个数据集来说,三个的分类器都一样足够好了吧,但是其实不然,这个只是训练集,现实测试的样本

  • python机器学习理论与实战（二）决策树

    python机器学习理论与实战（二）决策树

    决策树也是有监督机器学习方法. 电影<无耻混蛋>里有一幕游戏,在德军小酒馆里有几个人在玩20问题游戏,游戏规则是一个设迷者在纸牌中抽出一个目标(可以是人,也可以是物),而猜谜者可以提问题,设迷者只能回答是或者不是,在几个问题(最多二十个问题)之后,猜谜者通过逐步缩小范围就准确的找到了答案.这就类似于决策树的工作原理.(图一)是一个判断邮件类别的工作方式,可以看出判别方法很简单,基本都是阈值判断,关键是如何构建决策树,也就是如何训练一个决策树. (图一) 构建决策树的伪代码如下: Check i

  • python机器学习理论与实战（四）逻辑回归

    python机器学习理论与实战（四）逻辑回归

    从这节算是开始进入"正规"的机器学习了吧,之所以"正规"因为它开始要建立价值函数(cost function),接着优化价值函数求出权重,然后测试验证.这整套的流程是机器学习必经环节.今天要学习的话题是逻辑回归,逻辑回归也是一种有监督学习方法(supervised machine learning).逻辑回归一般用来做预测,也可以用来做分类,预测是某个类别^.^!线性回归想比大家都不陌生了,y=kx+b,给定一堆数据点,拟合出k和b的值就行了,下次给定X时,就可以计

  • python机器学习理论与实战（一）K近邻法

    机器学习分两大类,有监督学习(supervised learning)和无监督学习(unsupervised learning).有监督学习又可分两类:分类(classification.)和回归(regression),分类的任务就是把一个样本划为某个已知类别,每个样本的类别信息在训练时需要给定,比如人脸识别.行为识别.目标检测等都属于分类.回归的任务则是预测一个数值,比如给定房屋市场的数据(面积,位置等样本信息)来预测房价走势.而无监督学习也可以成两类:聚类(clustering)和密度估计

  • python接口自动化框架实战

    python接口自动化框架实战

    python接口测试的原理,就不解释了,百度一大堆. 先看目录,可能这个框架比较简单,但是麻雀虽小五脏俱全. 各个文件夹下的文件如下: 一.理清思路 我这个自动化框架要实现什么 1.从excel里面提取测试用例 2.测试报告的输出,并且测试报告得包括执行的测试用例的数量.成功的数量.失败的数量以及哪条成功了,失败的是哪一个,失败的原因是什么:测试结果的总体情况通过图表来表示. 3.测试报告用什么形式输出,excel,还是html,还是其他的,这里我选择了excel 4.配置文件需要配置什么东西

  • python matplotlib库绘图实战之绘制散点图

    python matplotlib库绘图实战之绘制散点图

    目录 一.导入库 二.设置文字 三.设置坐标轴参数 四.绘制点 五.对点的继续处理 1.自定义颜色 2.颜色映射 补充1 补充2 补充3 总结 一.导入库 import matplotlib.pyplot as plt 二.设置文字 plt.title("double number", fontsize=24) plt.xlabel("number", fontsize=14) plt.ylabel("double", fontsize=14)

  • Python爬虫框架Scrapy实战之批量抓取招聘信息

    Python爬虫框架Scrapy实战之批量抓取招聘信息

    网络爬虫抓取特定网站网页的html数据,但是一个网站有上千上万条数据,我们不可能知道网站网页的url地址,所以,要有个技巧去抓取网站的所有html页面.Scrapy是纯Python实现的爬虫框架,用户只需要定制开发几个模块就可以轻松的实现一个爬虫,用来抓取网页内容以及各种图片,非常之方便- Scrapy 使用wisted这个异步网络库来处理网络通讯,架构清晰,并且包含了各种中间件接口,可以灵活的完成各种需求.整体架构如下图所示: 绿线是数据流向,首先从初始URL 开始,Scheduler 会将其

  • 详解python解压压缩包的五种方法

    这里讨论使用Python解压例如以下五种压缩文件: .gz .tar  .tgz .zip .rar 简单介绍 gz: 即gzip.通常仅仅能压缩一个文件.与tar结合起来就能够实现先打包,再压缩. tar: linux系统下的打包工具.仅仅打包.不压缩 tgz:即tar.gz.先用tar打包,然后再用gz压缩得到的文件 zip: 不同于gzip.尽管使用相似的算法,能够打包压缩多个文件.只是分别压缩文件.压缩率低于tar. rar:打包压缩文件.最初用于DOS,基于window操作系统. 压缩

  • 详解Python Celery和RabbitMQ实战教程

    详解Python Celery和RabbitMQ实战教程

    前言 Celery是一个异步任务队列.它可以用于需要异步运行的任何内容.RabbitMQ是Celery广泛使用的消息代理.在本这篇文章中,我将使用RabbitMQ来介绍Celery的基本概念,然后为一个小型演示项目设置Celery .最后,设置一个Celery Web控制台来监视我的任务 基本概念   来!看图说话: Broker Broker(RabbitMQ)负责创建任务队列,根据一些路由规则将任务分派到任务队列,然后将任务从任务队列交付给worker Consumer (Celery Wo

随机推荐