python实现层次聚类的方法

层次聚类算法

顾名思义，层次聚类就是一层一层的进行聚类，可以由上向下把大的类别（cluster）分割，叫作分裂法；也可以由下向上对小的类别进行聚合，叫作凝聚法；但是一般用的比较多的是由下向上的凝聚方法。

分裂法：

分裂法指的是初始时将所有的样本归为一个类簇，然后依据某种准则进行逐渐的分裂，直到达到某种条件或者达到设定的分类数目。用算法描述：
输入：样本集合D，聚类数目或者某个条件（一般是样本距离的阈值，这样就可不设置聚类数目）
输出：聚类结果

1.将样本集中的所有的样本归为一个类簇；
repeat：
    2.在同一个类簇（计为c）中计算两两样本之间的距离，找出距离最远的两个样本a,b；
    3.将样本a，b分配到不同的类簇c1和c2中；
    4.计算原类簇（c）中剩余的其他样本点和a，b的距离，若是dis(a)<dis(b)，则将样本点归到c1中，否则归到c2中；
util： 达到聚类的数目或者达到设定的条件

凝聚法：

凝聚法指的是初始时将每个样本点当做一个类簇，所以原始类簇的大小等于样本点的个数，然后依据某种准则合并这些初始的类簇，直到达到某种条件或者达到设定的分类数目。用算法描述：
输入：样本集合D，聚类数目或者某个条件（一般是样本距离的阈值，这样就可不设置聚类数目）
输出：聚类结果

1.将样本集中的所有的样本点都当做一个独立的类簇；
   repeat：
        2.计算两两类簇之间的距离（后边会做介绍），找到距离最小的两个类簇c1和c2；
        3.合并类簇c1和c2为一个类簇；
   util： 达到聚类的数目或者达到设定的条件

例图：

欧式距离的计算公式

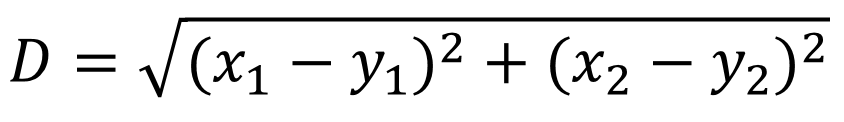
类簇间距离的计算方法有许多种：
(1)就是取两个类中距离最近的两个样本的距离作为这两个集合的距离，也就是说，最近两个样本之间的距离越小，这两个类之间的相似度就越大
(2)取两个集合中距离最远的两个点的距离作为两个集合的距离
(3)把两个集合中的点两两的距离全部放在一起求一个平均值，相对也能得到合适一点的结果。
e.g.下面是计算组合数据点(A,F)到(B,C)的距离，这里分别计算了(A,F)和(B,C)两两间距离的均值。

(4)取两两距离的中值，与取均值相比更加能够解除个别偏离样本对结果的干扰。
(5)求每个集合的中心点(就是将集合中的所有元素的对应维度相加然后再除以元素个数得到的一个向量)，然后用中心点代替集合再去就集合间的距离

实现

接下来以世界银行样本数据集进行简单实现。该数据集以标准格式存储在名为WBClust2013.csv的CSV格式的文件中。其有80行数据和14个变量。数据来源

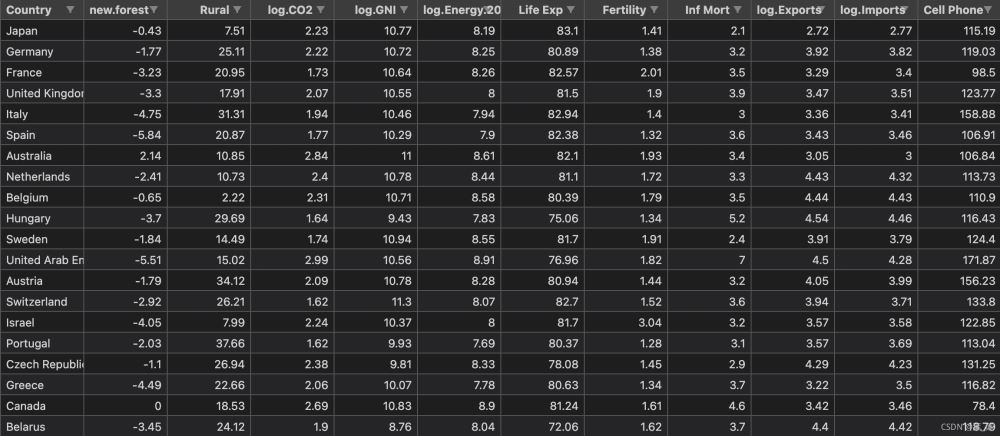
为了使得结果可视化更加方便，我将最后一栏人口数据删除了。并且在实现层次聚类之后加入PCA降维与原始结果进行对比。

from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

data = pd.read_csv('data/WBClust2013.csv')
data.pop('Pop')
# data.pop('RuralWater')
# data.pop('CellPhone')
# data.pop('LifeExp')
data = data[:20]
country = list(data['Country'])
data.pop('Country')

# 以下代码为仅使用层次聚类

plt.figure(figsize=(9, 7))
plt.title("original data")
mergings = linkage(data, method='average')
# print(mergings)
dendrogram(mergings, labels=country, leaf_rotation=45, leaf_font_size=8)
plt.show()
Z = linkage(data, method='average')
print(Z)
cluster_assignments = fcluster(Z, t=3.0, criterion='maxclust')
print(cluster_assignments)
for i in range(1, 4):
    print('cluster', i, ':')
    num = 1
    for index, value in enumerate(cluster_assignments):
        if value == i:
            if num % 5 == 0:
                print()
            num += 1
            print(country[index], end='  ')
    print()

# 以下代码为加入PCA进行对比
class myPCA():

    def __init__(self, X, d=2):
        self.X = X
        self.d = d

    def mean_center(self, data):
        """
        去中心化
        :param data: data sets
        :return:
        """
        n, m = data.shape
        for i in range(m):
            aver = np.sum(self.X[:, i])/n
            x = np.tile(aver, (1, n))
            self.X[:, i] = self.X[:, i]-x

    def runPCA(self):

        # 计算协方差矩阵，得到特征值，特征向量
        S = np.dot(self.X.T, self.X)
        S_val, S_victors = np.linalg.eig(S)
        index = np.argsort(-S_val)[0:self.d]
        Y = S_victors[:, index]
        # 得到输出样本集
        Y = np.dot(self.X, Y)
        return Y

# data_for_pca = np.array(data)
# pcaObject=myPCA(data_for_pca,d=2)
# pcaObject.mean_center(data_for_pca)
# res=pcaObject.runPCA()

# plt.figure(figsize=(9, 7))
# plt.title("after pca")
# mergings = linkage(res,method='average')
# print(mergings)
# dendrogram(mergings,labels=country,leaf_rotation=45,leaf_font_size=8)
# plt.show()
# Z = linkage(res, method='average')
# print(Z)
# cluster_assignments = fcluster(Z, t=3.0, criterion='maxclust')
# print(cluster_assignments)
# for i in range(1,4):
#     print('cluster', i, ':')
#     num = 1
#     for index, value in enumerate(cluster_assignments):
#         if value == i:
#             if num % 5 ==0:
#                 print()
#             num+=1
#             print(country[index],end='  ')
#     print()

两次分类结果都是一样的：

cluster 1 :
China  United States  Indonesia  Brazil
Russian Federation  Japan  Mexico  Philippines  Vietnam
Egypt, Arab Rep.  Germany  Turkey  Thailand  France
United Kingdom
cluster 2 :
India  Pakistan  Nigeria  Bangladesh
cluster 3 :
Ethiopia  

通过树状图对结果进行可视化

原始树状图：

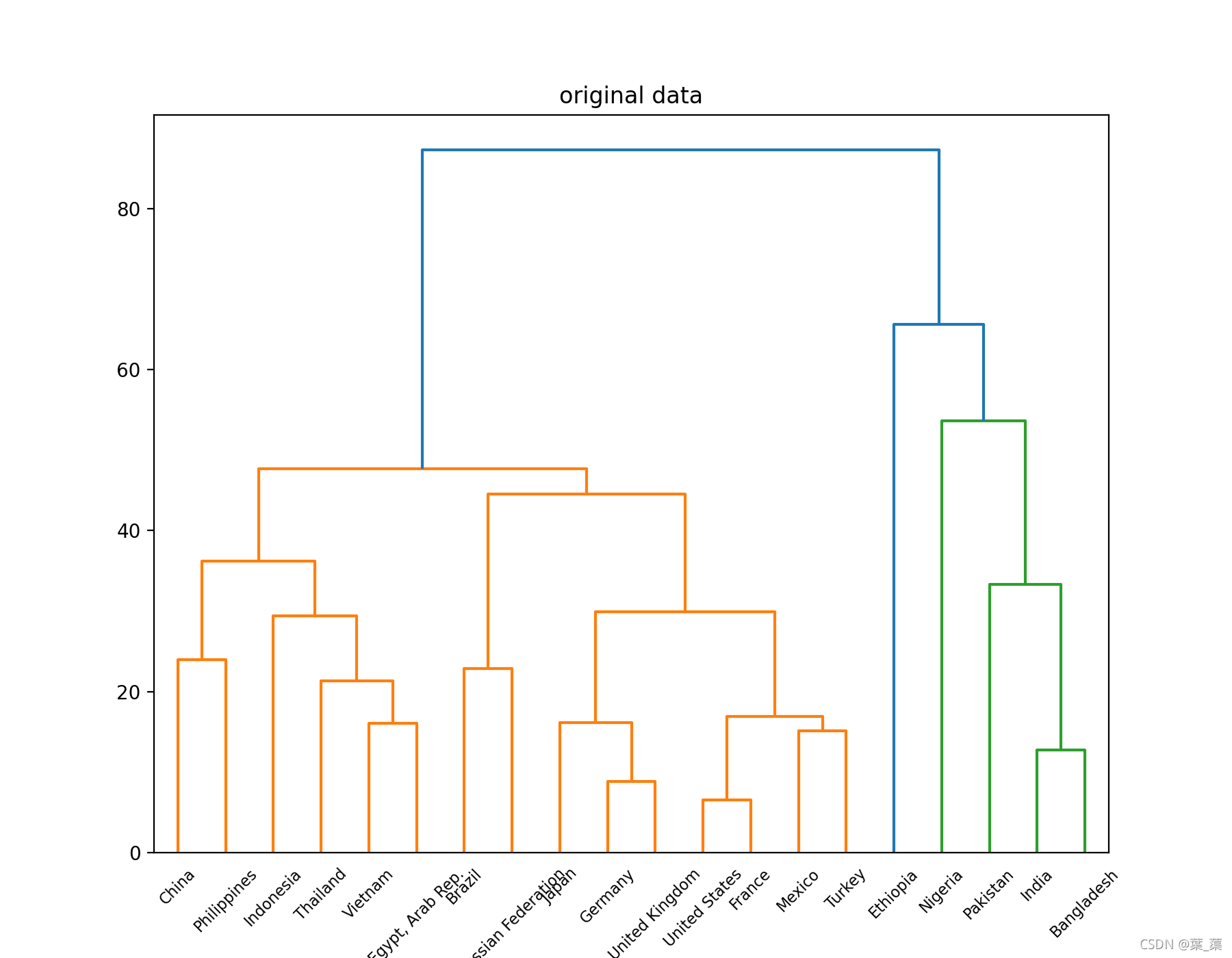
PCA降维后的结果：

到此这篇关于python实现层次聚类的文章就介绍到这了,更多相关python层次聚类内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！