Java基础之八大排序算法

前言

关系

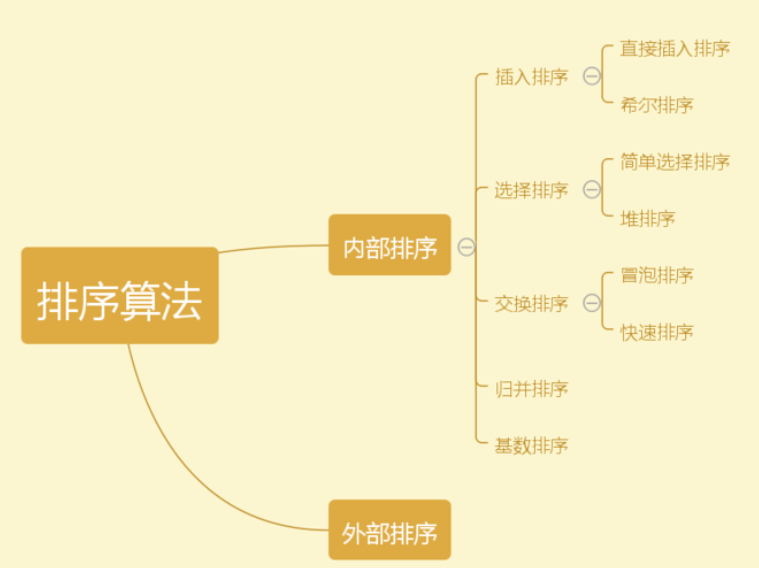
复杂度

一、直接插入排序

基本思想：

将新的数据插入已经排好的数据列中。

将第一个和第二个数排序，构成有序数列

然后将第三个数插进去，构成新的有序数列，后面的数重复这个步骤

算法描述

1、设定插入的次数，即是循环次数,for(int i=1;i<length;i++)，1个数的那次不用插入。

2、设定插入的数和得到的已经排好的序列的最后一个数,insertNum和j=i-1。

3、从最后一个数向前开始循环，如果插入数小于当前数就将当前数向前移动一位

4、将当前位置放置到空的位置，即j+1。

代码实现

public class Demo01 {
    public static void main(String[] args) {
        int [] data = {2,1,41,21,14,33,5};
        int temp; //要插入的数
        for (int i = 1; i < data.length; i++) {  // 插入的次数
            temp = data[i]; //要插入的数
            int j  = i-1;   //已经排好的数字
            while (j>=0&&data[j]>temp){ //判断后一个数，将大于要插入的数向后移动一格
                data[j+1] =data[j]; //元素移动一格
                j--;
            }
            data[j+1]=temp;     //将要插入的数字放入1插入的位置
        }
        for (int i = 0; i < data.length; i++) {
            System.out.print(data[i]+" ");
        }
    }
}

二、希尔排序

基本思想：

对于直接插入的数，数据量巨大：

1.将数的个数设置为n，取奇数k = n/2,将下标的差值k的数分为一组，构成有序数列。

2.再取k = k/2,将下标差值为k的数构成一组，构成有序数列，

3.重复第二步，直到k=1执行简单的插入排序

算法描述

1.首先确定分组的数字

2.然后对组中的数字进行插入排序

3.然后将length/2，重复1,2步骤。直到length=0为止。

代码实现

public class Demo02 {
    public static void main(String[] args) {
        int [] data = {2,5,14,34,12,4,87,21,1,6};
        int d = data.length;
        while (d!=0){
            d = d/2;
            for (int x = 0; x < d; x++) {
                for (int i = d+x; i < data.length; i += d) {
                    int j = i - d;      //j为有序序列最后一位的位数
                    int temp = data[i]; //要插入的元素
                    for (;j>=0&&temp < data[j]; j -=d){
                        data[j+d]=data[j]; //向后移动d位
                    }
                    data[j+d] = temp;
                }
            }
        }
        for (int i = 0; i < data.length; i++) {
            System.out.print(data[i]+" ");
        }

    }
}

三、简单选择排序

基本思想：

常用于取序列数中最大最小的几棵树

(如果每次比较都交换，那么就是交换排序；如果每次比较完一个循环再交换，就是简单选择排序。)

1.遍历整个序列，将最小的数放在最前面

2.遍历剩余的序列，将最小的数字放在最前面

3.重复步骤2，知道剩余最后一个数字。

算法描述

1.首先确定循环次数，并且记住当前的位置和当前数字

2.将当前位置后面的所有数字和当前位置的数字作比较，小数赋值给key,并记住小值的位置

3.比对完成后，将最小的值和第一个数的值交换

4.重复2,3步骤

代码实现

public class Demo03 {
    public static void main(String[] args) {
        int[] data = {2,6,123,56,23,1};
        for (int i = 0; i < data.length; i++) { //循环次数
            int key = data[i];//最小值
            int position=i;  //当前位置
            for (int j = i+1; j < data.length; j++) {//选出最小值
                if(data[j]<key){
                    key = data[j];
                    position =j;
                }
            }
            data[position] = data[i];//交换位置
            data[i] = key;
        }
        for (int i = 0; i < data.length; i++) {
            System.out.print(data[i]+" ");
        }
    }
}

四、堆排序

基本思想：

对简单选择排序的优化

1.将序列构建为大顶堆

2.将根节点与最后一个节点兑换，然后断开最后一个节点

3.重复一二步骤，直到所有节点断开

代码实现：

public class Demo04 {
    public static void main(String[] args) {
        int []data = {21,13,3,2,1,23,11,25};
        heapsort(data);
    }
    public static void heapsort(int a[]){
        System.out.println("开始排序");
        int arrayLength = a.length;
        for (int i = 0; i < arrayLength-1; i++) {
            buildMaxHeap(a,arrayLength-1-i);
            swap(a,0,arrayLength-1-i);
            System.out.println(Arrays.toString(a));
        }
    }
    private static void swap(int[] data, int i, int j) {
        // TODO Auto-generated method stub
        int tmp=data[i];
        data[i]=data[j];
        data[j]=tmp;
    }

    public static void buildMaxHeap(int[] data,int lastIndex){
        //从lastIndex处节点（最后一个节点）的父节点开始
        for (int i = (lastIndex-1)/2;i>=0;i--){
            //k 保存当前判断的节点
            int k = i;
//            如果当前k节点存在子节点
            while (k*2+1<=lastIndex){
//                k节点的左子节点的索引
                int biggerIndex = 2*k+1;
//                如果biggerIndex小于lastIndex，即biggerIndex+1代表的k节点的右子节点存在
                if (biggerIndex<lastIndex){
//                    如果右子节点的值较大
                    if(data[biggerIndex]<data[biggerIndex+1]){
                        biggerIndex++;
                    }
                }
//                如果k节点的值小于其较大的子节点的值
                if (data[k]<data[biggerIndex]){
                    swap(data,k,biggerIndex);
                    k = biggerIndex;
                }else {
                    break;
                }
            }
        }
    }
}

五、冒泡排序

基本思想

1.将序列中所有的元素两两比较

2.将剩余序列的所有元素两两比较，将最大的放到最后面

3.重复第二步，知道最后一个数

算法描述

1.设置循环次数

2.设置比较的位数和结束的位数

3.两两比较，将最小的放到前面去

4.重复2，3步骤，直到循环结束

代码实现

public class Demo05 {
    public static void main(String[] args) {
        int[] data={1,34,31,2,65,87,255,8,33,64,3};
       int temp;
        for (int i = 0; i < data.length; i++) {
            for (int j = 0; j < data.length-i-1; j++) {
                if(data[j] > data[j+1]){
                    temp = data[j];
                    data[j] = data[j+1];
                    data[j+1] = temp;
                }
            }
        }
        for (int i = 0; i < data.length; i++) {
            System.out.print(data[i]+" ");
        }
    }
}

六、快速排序

基本思想

要求时间最快

1.选择第一个数作为P,小于P的放左边，大于p的放右边

2.递归将p的左边和右边的数按照步骤一进行，直到不能递归

代码实现

public class Demo06 {
    public static void main(String[] args) {
        int[] data = {5,33,22,11,23,2,32,12,21,10};
        quickSort(data,0,data.length-1);
        sorts(data);
    }
    public static void quickSort(int[] data,int L,int R){
        if(L < R){
//            先选择比较的基数
            int base = data[L];
            int temp;
            int left=L,right=R;
            do{
                while ((data[left] < base) && (left < R)){
                    left++;
                }
                while ((data[right]) > base &&(right > L)){
                    right--;
                }
                if (left <= right){
                    temp = data[left];
                    data[left] = data[right];
                    data[right] = temp;
                    left++;
                    right--;
                }
            }while (left <= right);
            if (L < right){
                quickSort(data,L,right);
            }
            if (R > left){
                quickSort(data,left,R);
            }
        }
    }
    public static void sorts(int[] data){
        for (int i = 0; i < data.length; i++) {
            if (i == data.length-1){
                System.out.print(data[i]);
            }else {
                System.out.print(data[i]+",");
            }

        }
    }
}

七、归并排序

基本思想

速度仅次于快排，内存少的时候使用，可以进行并行运算的时候使用。

1.选择相邻两个数组成的有序序列

2.选择相邻的两个有序序列组成的一个有序序列

3.重复步骤二，直到组成一个有序序列

public class Demo0701 {
    public static void main(String[] args) {
        int[] arr = {12,34,3,2,13,43,34,25,83};
        mSort(arr, 0, arr.length-1);
        sorts(arr);
    }

    /**
     * 递归分治
     * @param arr 待排数组
     * @param left 左指针
     * @param right 右指针
     */
    public static void mSort(int[] arr, int left, int right) {
        if(left >= right)
            return ;
        int mid = (left + right) / 2;

        mSort(arr, left, mid); //递归排序左边
        mSort(arr, mid+1, right); //递归排序右边
        merge(arr, left, mid, right); //合并
    }

    /**
     * 合并两个有序数组
     * @param arr 待合并数组
     * @param left 左指针
     * @param mid 中间指针
     * @param right 右指针
     */
    public static void merge(int[] arr, int left, int mid, int right) {
        //[left, mid] [mid+1, right]
        int[] temp = new int[right - left + 1]; //中间数组
        int i = left;
        int j = mid + 1;
        int k = 0;

        //执行完这个while循环，相当于将两个子序列合并后重新进行了一次排序并将排序结果记录在了临时数组temp[k]中。
        // while走完后k的值等于数组的长度，i的值此时大于mid，j的值大于right
        while(i <= mid && j <= right) {
            if(arr[i] <= arr[j]) {
                temp[k++] = arr[i++];
            }
            else {
                temp[k++] = arr[j++];
            }
        }

        while(i <= mid) {
            temp[k++] = arr[i++];
        }

        while(j <= right) {
            temp[k++] = arr[j++];
        }

        //将有序的临时数组temp[k]一个一个赋值到原数组arr[]中
        for(int p=0; p<temp.length; p++) {
            arr[left + p] = temp[p];
        }
    }
    public static void sorts(int[] data){
        for (int i = 0; i < data.length; i++) {
            if (i == data.length-1){
                System.out.print(data[i]);
            }else {
                System.out.print(data[i]+",");
            }
        }
    }
}

八、基数排序(桶排序)

基本思想

用于大量数，很长数进行排列

1.将所有的数的个数取出来，按照个位数排序，构成序列

2.将新构成的所有数的十位数取出，按照十位数进行排序

代码实现

public class Demo08 {
    public static void main(String[] args) {
        int[] data = {12,34,3,2,13,43,34,25,83};
        if(data == null && data.length == 0)
            return ;

        int maxBit = getMaxBit(data);

        for(int i=1; i<=maxBit; i++) {

            List<List<Integer>> buf = distribute(data, i); //分配
            collecte(data, buf); //收集
        }
        new PrintSort(data);
    }

    /**
     * 分配
     * @param arr 待分配数组
     * @param iBit 要分配第几位
     * @return
     */
    public static List<List<Integer>> distribute(int[] arr, int iBit) {
        List<List<Integer>> buf = new ArrayList<List<Integer>>();
        for(int j=0; j<10; j++) {
            buf.add(new LinkedList<Integer>());
        }
        for(int i=0; i<arr.length; i++) {
            buf.get(getNBit(arr[i], iBit)).add(arr[i]);
        }
        return buf;
    }

    /**
     * 收集
     * @param arr 把分配的数据收集到arr中
     * @param buf
     */
    public static void collecte(int[] arr, List<List<Integer>> buf) {
        int k = 0;
        for(List<Integer> bucket : buf) {
            for(int ele : bucket) {
                arr[k++] = ele;
            }
        }

    }

    /**
     * 获取最大位数
     * @param
     * @return
     */
    public static int getMaxBit(int[] arr) {
        int max = Integer.MIN_VALUE;
        for(int ele : arr) {
            int len = (ele+"").length();
            if(len > max)
                max = len;
        }
        return max;
    }

    /**
     * 获取x的第n位，如果没有则为0.
     * @param x
     * @param n
     * @return
     */
    public static int getNBit(int x, int n) {
        String sx = x + "";
        if(sx.length() < n)
            return 0;
        else
            return sx.charAt(sx.length()-n) - '0';
    }
}

到此这篇关于Java基础之八大排序算法的文章就介绍到这了,更多相关java八大排序算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！