Python 确定多项式拟合/回归的阶数实例

通过 1至10 阶来拟合对比 均方误差及R评分，可以确定最优的“最大阶数”。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression,Perceptron
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.model_selection import train_test_split

X = np.array([-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10]).reshape(-1, 1)
y = np.array(2*(X**4) + X**2 + 9*X + 2)
#y = np.array([300,500,0,-10,0,20,200,300,1000,800,4000,5000,10000,9000,22000]).reshape(-1, 1)

x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
rmses = []
degrees = np.arange(1, 10)
min_rmse, min_deg,score = 1e10, 0 ,0

for deg in degrees:
	# 生成多项式特征集(如根据degree=3 ,生成 [[x,x**2,x**3]] )
	poly = PolynomialFeatures(degree=deg, include_bias=False)
	x_train_poly = poly.fit_transform(x_train)

	# 多项式拟合
	poly_reg = LinearRegression()
	poly_reg.fit(x_train_poly, y_train)
	#print(poly_reg.coef_,poly_reg.intercept_) #系数及常数

	# 测试集比较
	x_test_poly = poly.fit_transform(x_test)
	y_test_pred = poly_reg.predict(x_test_poly)

	#mean_squared_error(y_true, y_pred) #均方误差回归损失,越小越好。
	poly_rmse = np.sqrt(mean_squared_error(y_test, y_test_pred))
	rmses.append(poly_rmse)
	# r2 范围[0，1]，R2越接近1拟合越好。
	r2score = r2_score(y_test, y_test_pred)

	# degree交叉验证
	if min_rmse > poly_rmse:
		min_rmse = poly_rmse
		min_deg = deg
		score = r2score
	print('degree = %s, RMSE = %.2f ,r2_score = %.2f' % (deg, poly_rmse,r2score))

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(degrees, rmses)
ax.set_yscale('log')
ax.set_xlabel('Degree')
ax.set_ylabel('RMSE')
ax.set_title('Best degree = %s, RMSE = %.2f, r2_score = %.2f' %(min_deg, min_rmse,score))
plt.show()

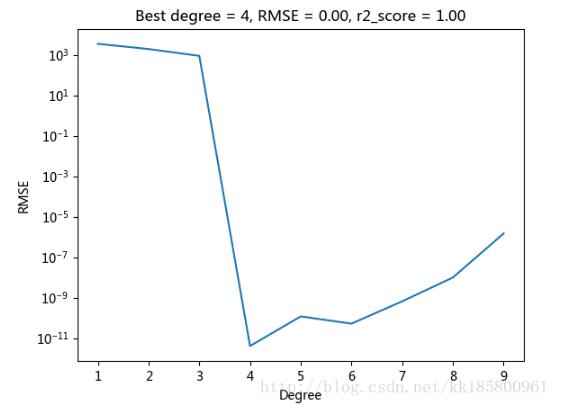
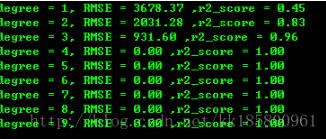
因为因变量 Y = 2*(X**4) + X**2 + 9*X + 2 ，自变量和因变量是完整的公式，看图很明显，degree >=4 的都符合，拟合函数都正确。（RMSE 最小，R平方非负且接近于1，则模型最好）

如果将 Y 值改为如下：

y = np.array([300,500,0,-10,0,20,200,300,1000,800,4000,5000,10000,9000,22000]).reshape(-1, 1)

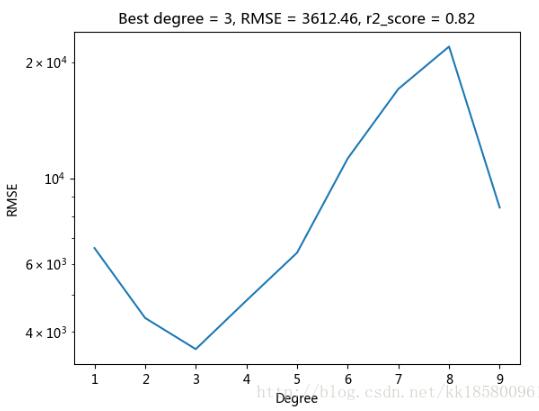
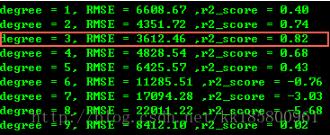
degree=3 是最好的，且 r 平方也最接近于1（注意：如果 R 平方为负数，则不准确，需再次测试。因样本数据较少，可能也会判断错误）。

以上这篇Python 确定多项式拟合/回归的阶数实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。