python机器学习高数篇之泰勒公式

不少同学一提到泰勒公式，脑海里立马浮现高大上的定义和长长的公式，令人望而生畏。

实际上，泰勒公式没有那么可怕，它是用简单的多项式来逼近一个光滑的函数，从而近似替代不熟悉的函数。由于泰勒公式具有将复杂函数近似成多个幂函数叠加形式的性质，可以用它进行比较、求极限、求导、解微分方程等。

我们先来看一下泰勒公式的发明者，布鲁克·泰勒——

布鲁克·泰勒（Brook Taylor,1685-1732）,英国数学家，牛顿学派最优秀的代表人物之一，他于1712年的一封信里首次叙述了泰勒公式。

再来看一下高数书上对泰勒公式的定义：

公式3-5就称为f(x)在x0处的带有拉格朗日余项的n阶泰勒公式。

初看这个泰勒公式的定义，就觉得恢宏大气，气势磅礴。不过光从泰勒公式的定义，很难直观看出它是怎么用多项式逼近原函数的。接下来我们用图像和图表来感受一下——

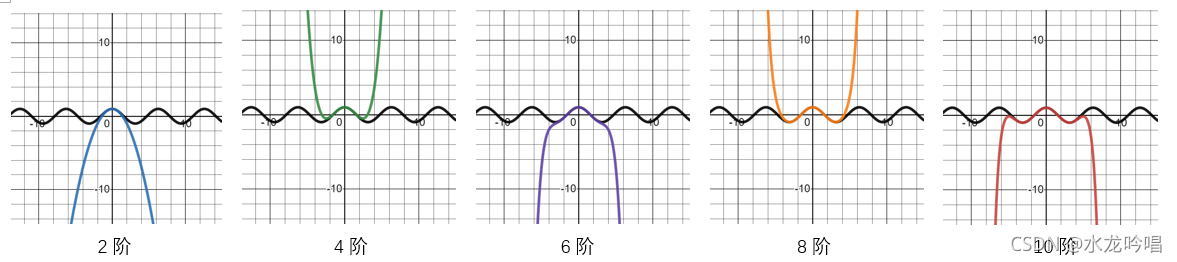
这里我们先列举出f(x) = cosx在原点的泰勒2阶、4阶、6阶、8阶、10阶的多项式，并用图像表示该函数及其泰勒n阶多项式。

对应图像如下，其中黑色线条为原函数f(x)，彩色线条为多项式g(x)。可以看到随着阶数的增大，多项式在更大范围内越来越逼近原函数。

我们再用python实现函数y=cosx的泰勒n阶多项式，并与y=cosx的实际值进行比较，其中令n=40。

def f_cos(x):
    m = 20+1
    sum = 1.0
    for i in range(1,m): #range函数取值是左闭右开
        n = 2 * i
        tmp1,tmp2,tmp3 = 1,1,1
        for j in range(1,i+1):
            tmp1 = -tmp1
        for j in range(1,n+1):
            tmp2 = tmp2*x
            tmp3 = tmp3*j
        sum = sum + tmp1*tmp2/tmp3
    return sum

from numpy import *
for x in range(-20,21):
    print("x = " + str(x))
    print("f_cos(x) = " + str(f_cos(x)))
    print("cos(x) = " + str(cos(x)))

比较自定义的f_cos(x)和numpy库的cosx的误差：

x取值 自定义的f_cos(x) numpy库的cosx 误差（f_cos(x) - cos(x)） 分析
20 2577.3069 0.4081 2576.8988 误差非常大
19 305.1701 0.9887 304.1814 误差较大
18 32.5969 0.6603 31.9366 存在误差
17 2.6676 -0.2752 2.9428 存在误差
16 -0.7234 -0.9577 0.2343 存在0.1级误差
15 -0.7439 -0.7597 0.0158 存在0.01级误差
14 0.1376 0.1367 0.0009 存在0.0001级误差
13 0.9075 0.9074 0.0000 精度范围内一致
12 0.8439 0.8439 0.0000 精度范围内一致
11 0.0044 0.0044 0.0000 精度范围内一致
10 -0.8391 -0.8391 0.0000 精度范围内一致
9 -0.9111 -0.9111 0.0000 精度范围内一致
8 -0.1455 -0.1455 0.0000 精度范围内一致
7 0.7539 0.7539 0.0000 精度范围内一致
6 0.9602 0.9602 0.0000 精度范围内一致
5 0.2837 0.2837 0.0000 精度范围内一致
4 -0.6536 -0.6536 0.0000 精度范围内一致
3 -0.9900 -0.9900 0.0000 精度范围内一致
2 -0.4161 -0.4161 0.0000 精度范围内一致
1 0.5403 0.5403 0.0000 精度范围内一致
0 1.0000 1.0000 0.0000 精度范围内一致

由于f(x) = cosx函数关于y轴对称，这里只列举出了x轴右半部分[0,20]的范围，x轴左半部分的结果与右半部分结果相同。

在[0,20]范围内，当x=20时，二者的误差非常大。随着x的减小，二者的误差也在逐渐减小。在[0,13]范围内，二者在精度范围内完全一致，几乎零误差。

大家可以尝试一下，把n的值调大，这个精度一致的范围会变大。例如此例若n=30，即y=cosx的泰勒30阶多项式，则在[-20,20]范围内，二者精度都完全一致。感兴趣的同学可以运用同样的方法，分析一下其他函数。

再试着写出函数y=sinx的泰勒n阶多项式的python程序，其中n=19。

def f_sin(x):
    m = 10+1
    sum = 0.0
    for i in range(1,m):
        n = 2 * i - 1
        tmp1,tmp2,tmp3 = 1,1,1
        for j in range(1,i):
            tmp1 = -tmp1
        for j in range(1,n+1):
            tmp2 = tmp2*x
            tmp3 = tmp3*j
        sum = sum + tmp1*tmp2/tmp3
    return sum

from numpy import *
for x in range(-20,21):
    print("x = " + str(x))
    print("f_sin(x) = " + str(f_sin(x)))
    print("sin(x) = " + str(sin(x)))

后续会继续增加一些函数的泰勒n阶多项式python程序（可能会偷懒）。

最后推荐一个比较好用的在线画函数的工具Desmos：

https://www.desmos.com/calculator?lang=zh-CN

简易教程:

https://www.ravenxrz.ink/archives/27d14722.html

还可以用著名的心形线画个爱心哦：

到此这篇关于python机器学习高数篇之泰勒公式的文章就介绍到这了,更多相关python泰勒公式内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • Python机器学习入门(五)算法审查

    Python机器学习入门(五)算法审查

    目录 1.审查分类算法 1.1线性算法审查 1.1.1逻辑回归 1.1.2线性判别分析 1.2非线性算法审查 1.2.1K近邻算法 1.2.2贝叶斯分类器 1.2.4支持向量机 2.审查回归算法 2.1线性算法审查 2.1.1线性回归算法 2.1.2岭回归算法 2.1.3套索回归算法 2.1.4弹性网络回归算法 2.2非线性算法审查 2.2.1K近邻算法 2.2.2分类与回归树 2.2.3支持向量机 3.算法比较 总结 程序测试是展现BUG存在的有效方式,但令人绝望的是它不足以展现其缺位. --

  • Python机器学习入门(四)选择模型

    Python机器学习入门(四)选择模型

    目录 1.数据分离与验证 1.1分离训练数据集和评估数据集 1.2K折交叉验证分离 1.3弃一交叉验证分离 1.4重复随机分离评估数据集与训练数据集 2.算法评估 2.1分类算法评估 2.1.1分类准确度 2.1.2分类报告 2.2回归算法评估 2.2.1平均绝对误差 2.2.2均方误差 2.2.3判定系数() 总结 1.数据分离与验证 要知道算法模型对未知的数据表现如何,最好的评估办法是利用已经明确知道结果的数据运行生成的算法模型进行验证.此外还可以使用新的数据来评估算法模型. 在评估机器学习

  • python机器学习高数篇之函数极限与导数

    python机器学习高数篇之函数极限与导数

    不知道大家有没有类似的经历,斗志满满地翻开厚厚的机器学习书,很快被一个个公式炸蒙了. 想要学习机器学习算法,却很难看的懂里面的数学公式,实际应用只会调用库里的函数,无法优化算法. 学好机器学习,没有数学知识是不行的.数学知识的积累是一个漫长的过程,罗马也不是一夜建成的. 如果想要入门机器学习,数学基础比较薄弱,想打牢相关数学基础,可以关注笔者,一起学习(数学大佬也可以来扫一眼python代码)~ 接下来我们以高数(同济第七版)课后习题为例,使用python语言来求解函数和导数的习题. 这样大家做

  • Python机器学习入门(一)序章

    Python机器学习入门(一)序章

    目录 前言 写在前面 1.什么是机器学习? 1.1 监督学习 1.2无监督学习 2.Python中的机器学习 3.必须环境安装 Anacodna安装 总结 前言 每一次变革都由技术驱动.纵观人类历史,上古时代,人类从采集狩猎社会,进化为农业社会:由农业社会进入到工业社会:从工业社会到现在信息社会.每一次变革,都由新技术引导. 在历次的技术革命中,一个人.一家企业,甚至一个国家,可以选择的道路只有两条:要么加入时代的变革,勇立潮头:要么徘徊观望,抱憾终生. 要想成为时代弄潮儿,就要积极拥抱这次智能

  • Python机器学习入门(二)数据理解

    Python机器学习入门(二)数据理解

    目录 1.数据导入 1.1使用标准Python类库导入数据 1.2使用Numpy导入数据 1.3使用Pandas导入数据 2.数据理解 2.1数据基本属性 2.1.1查看前10行数据 2.1.2查看数据维度,数据属性和类型: 2.1.3查看数据描述性统计 2.2数据相关性和分布分析 2.2.1数据相关矩阵 2.2.2数据分布分析 3.数据可视化 3.1单一图表 3.1.1直方图 3.1.2密度图 3.1.3箱线图 3.2多重图表 3.2.1相关矩阵图 3.2.2散点矩阵图 总结 统计学是什么?概

  • Python机器学习入门(六)优化模型

    Python机器学习入门(六)优化模型

    目录 1.集成算法 1.1袋装算法 1.1.1袋装决策树 1.1.2随机森林 1.1.3极端随机树 1.2提升算法 1.2.1AdaBoost 1.2.2随机梯度提升 1.3投票算法 2.算法调参 2.1网络搜索优化参数 2.2随机搜索优化参数 总结 有时提升一个模型的准确度很困难.你会尝试所有曾学习过的策略和算法,但模型正确率并没有改善.这时你会觉得无助和困顿,这也正是90%的数据科学家开始放弃的时候.不过,这才是考验真正本领的时候!这也是普通的数据科学家和大师级数据科学家的差距所在. 1.集

  • Python机器学习入门(三)数据准备

    目录 1.数据预处理 1.1调整数据尺度 1.2正态化数据 1.3标准化数据 1.4二值数据 2.数据特征选定 2.1单变量特征选定 2.2递归特征消除 2.3数据降维 2.4特征重要性 总结 特征选择时困难耗时的,也需要对需求的理解和专业知识的掌握.在机器学习的应用开发中,最基础的是特征工程. --吴恩达 1.数据预处理 数据预处理需要根据数据本身的特性进行,有缺失的要填补,有无效的要剔除,有冗余维的要删除,这些步骤都和数据本身的特性紧密相关. 1.1调整数据尺度 如果数据的各个属性按照不同的

  • python机器学习高数篇之泰勒公式

    python机器学习高数篇之泰勒公式

    不少同学一提到泰勒公式,脑海里立马浮现高大上的定义和长长的公式,令人望而生畏. 实际上,泰勒公式没有那么可怕,它是用简单的多项式来逼近一个光滑的函数,从而近似替代不熟悉的函数.由于泰勒公式具有将复杂函数近似成多个幂函数叠加形式的性质,可以用它进行比较.求极限.求导.解微分方程等. 我们先来看一下泰勒公式的发明者,布鲁克·泰勒-- 布鲁克·泰勒(Brook Taylor,1685-1732),英国数学家,牛顿学派最优秀的代表人物之一,他于1712年的一封信里首次叙述了泰勒公式. 再来看一下高数书上

  • Python机器学习应用之基于LightGBM的分类预测篇解读

    Python机器学习应用之基于LightGBM的分类预测篇解读

    目录 一.Introduction 1 LightGBM的优点 2 LightGBM的缺点 二.实现过程 1 数据集介绍 2 Coding 三.Keys LightGBM的重要参数 基本参数调整 针对训练速度的参数调整 针对准确率的参数调整 针对过拟合的参数调整 一.Introduction LightGBM是扩展机器学习系统.是一款基于GBDT(梯度提升决策树)算法的分布梯度提升框架.其设计思路主要集中在减少数据对内存与计算性能的使用上,以及减少多机器并行计算时的通讯代价 1 LightGBM

  • Python机器学习应用之基于天气数据集的XGBoost分类篇解读

    Python机器学习应用之基于天气数据集的XGBoost分类篇解读

    目录 一.XGBoost 1 XGBoost的优点 2 XGBoost的缺点 二.实现过程 1 数据集 2 实现 三.Keys XGBoost的重要参数 一.XGBoost XGBoost并不是一种模型,而是一个可供用户轻松解决分类.回归或排序问题的软件包. 1 XGBoost的优点 简单易用.相对其他机器学习库,用户可以轻松使用XGBoost并获得相当不错的效果. 高效可扩展.在处理大规模数据集时速度快效果好,对内存等硬件资源要求不高. 鲁棒性强.相对于深度学习模型不需要精细调参便能取得接近的

  • Python机器学习应用之基于决策树算法的分类预测篇

    Python机器学习应用之基于决策树算法的分类预测篇

    目录 一.决策树的特点 1.优点 2.缺点 二.决策树的适用场景 三.demo 一.决策树的特点 1.优点 具有很好的解释性,模型可以生成可以理解的规则. 可以发现特征的重要程度. 模型的计算复杂度较低. 2.缺点 模型容易过拟合,需要采用减枝技术处理. 不能很好利用连续型特征. 预测能力有限,无法达到其他强监督模型效果. 方差较高,数据分布的轻微改变很容易造成树结构完全不同. 二.决策树的适用场景 决策树模型多用于处理自变量与因变量是非线性的关系. 梯度提升树(GBDT),XGBoost以及L

  • Python机器学习应用之支持向量机的分类预测篇

    Python机器学习应用之支持向量机的分类预测篇

    目录 1.Question? 2.Answer!——SVM 3.软间隔 4.超平面 支持向量机常用于数据分类,也可以用于数据的回归预测 1.Question? 我们经常会遇到这样的问题,给你一些属于两个类别的数据(如子图1),需要一个线性分类器将这些数据分开,有很多分法(如子图2),现在有一个问题,两个分类器,哪一个更好?为了判断好坏,我们需要引入一个准则:好的分类器不仅仅能够很好的分开已有的数据集,还能对为知的数据进行两个划分,假设现在有一个属于红色数据点的新数据(如子图3中的绿三角),可以看

  • Python机器学习应用之基于BP神经网络的预测篇详解

    Python机器学习应用之基于BP神经网络的预测篇详解

    目录 一.Introduction 1 BP神经网络的优点 2 BP神经网络的缺点 二.实现过程 1 Demo 2 基于BP神经网络的乳腺癌分类预测 三.Keys 一.Introduction 1 BP神经网络的优点 非线性映射能力:BP神经网络实质上实现了一个从输入到输出的映射功能,数学理论证明三层的神经网络就能够以任意精度逼近任何非线性连续函数.这使得其特别适合于求解内部机制复杂的问题,即BP神经网络具有较强的非线性映射能力. 自学习和自适应能力:BP神经网络在训练时,能够通过学习自动提取输

  • Python机器学习应用之工业蒸汽数据分析篇详解

    Python机器学习应用之工业蒸汽数据分析篇详解

    目录 一.数据集 二.数据分析 1 数据导入 2 数据特征探索(数据可视化) 三.特征优化 四.对特征构造后的训练集和测试集进行主成分分析 五.使用LightGBM模型进行训练和预测 一.数据集 1. 训练集 提取码:1234 2. 测试集 提取码:1234 二.数据分析 1 数据导入 #%%导入基础包 import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from

  • Python机器学习应用之基于线性判别模型的分类篇详解

    Python机器学习应用之基于线性判别模型的分类篇详解

    目录 一.Introduction 1 LDA的优点 2 LDA的缺点 3 LDA在模式识别领域与自然语言处理领域的区别 二.Demo 三.基于LDA 手写数字的分类 四.小结 一.Introduction 线性判别模型(LDA)在模式识别领域(比如人脸识别等图形图像识别领域)中有非常广泛的应用.LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的.这点和PCA不同.PCA是不考虑样本类别输出的无监督降维技术. LDA的思想可以用一句话概括,就是"投影后类内方差最小,类间方

  • Python机器学习应用之朴素贝叶斯篇

    Python机器学习应用之朴素贝叶斯篇

    朴素贝叶斯(Naive Bayes,NB):朴素贝叶斯分类算法是学习效率和分类效果较好的分类器之一.朴素贝叶斯算法一般应用在文本分类,垃圾邮件的分类,信用评估,钓鱼网站检测等. 1.鸢尾花案例 #%%库函数导入 import warnings warnings.filterwarnings('ignore') import numpy as np # 加载莺尾花数据集 from sklearn import datasets # 导入高斯朴素贝叶斯分类器 from sklearn.naive_b

随机推荐