C语言深入探究选择排序与基数排序使用案例讲解

目录

• 一.选择排序
• 1.1 选择排序引入
• 1.2 选择排序的基本思想与算法分析
• 1.3 实例说明
• 1.4 代码实现
• 1.5 性能分析
• 二.基数排序
• 2.1 基数排序基本思想与算法步骤
• 2.2 实例说明
• 2.3 代码实现
• 2.4 性能分析

一.选择排序

1.1 选择排序引入

就像炒股一样，有的人爱炒短线，不断的买进卖出通过差价来盈利，但是频繁的买进卖出，也会因为频繁的手续费和一系列费用获益较少；有的人，不断的进行观察和判断，等到时机一到，果断买进或卖出，这种人交易次数少，而最终收获颇丰；正如我们所说的第一种人就类似排序里的冒泡排序，而第二种人就在排序中可以理解为：在排序时找到合适的关键字再做交换，并且只交换一次完成相应关键字的排序；这就是我们要说的选择排序。

1.2 选择排序的基本思想与算法分析

基本思想：从头至尾扫描序列，找出最小的一个元素，和第一个元素交换，接着从剩下的元素中继续这种选择和交换方式，最终得到一个有序序列

算法分析：

1. 第1步:在未排序的n个数(a [0] ~a [n- 1])中找到最小数，将它与a [0]交换;
2. 第2步:在剩下未排序的n- 1个数(a [1] ~a [n- 1])中找到最小数，将它与a[1]交换;
3. 第n-1步:在剩下未排序的2个数(a [n-2] ~a [n- 1] )中找到最小数，将它与a [n-2]交换；
4. 得到一个排好序的序列。

1.3 实例说明

以12，32，2，60，42，98为例，排序过程如下：

• 数字底下有横线的为已排好序的
• n个值排n-1次即可
• 每一次都找一个最小值放到前面

1.4 代码实现

代码如下：

void SelectSort(int arr[], int len)
{
	for (int i = 0; i < len - 1; i++)//趟数
	{
		int min_index = i;
		for (int j = i + 1; j < len; j++)//控制找最小值
		{
			if (arr[j] < arr[min_index])
			{
				min_index = j;
			}
		}
		//当内层for循环跑完，此时min_index保存是就是当前待排序序列中最小值的下标
		if (min_index != i)//如果找到的最小值下标  不等于 待排序序列的第一个值的下标  则才有交换的必要性
		{
			int tmp = arr[i];
			arr[i] = arr[min_index];
			arr[min_index] = tmp;
		}
	}
}

1.5 性能分析

• 时间复杂度：O（n^2）。
• 空间复杂度：O（1）。
• 稳定性：不稳定。

尽管与冒泡排序的时间复杂度同为O（n^2），但选择排序的性能还是略优于冒泡排序的。

二.基数排序

2.1 基数排序基本思想与算法步骤

基本思想：将整数按位数切割成不同的数字，然后按每个位数分别比较，最后合并结果。

算法步骤：

• 将所有待比较数值统一为同样的数位长度，数位较短的数前面补零；
• 从最低位开始，依次进行一次排序；
• 从最低位排序一直到最高位排序完成以后, 整合后数列就变成一个有序序列。

2.2 实例说明

以12，32，2，620，42，98，122，289，987，37，56，90为例，排序过程如下：

1.以个位数跑一趟：

个位排序的最终结果：

620，90，12，32，2，42，122，56，987，27，98，289

（这些数据只看个位的话为有序）

2.以十位跑一趟：

十位排序的最终结果：

2，12，620，122，27，32，43，56，987，289，90，98

（这些数据只看十位的话为有序）

3.以百位跑一趟：

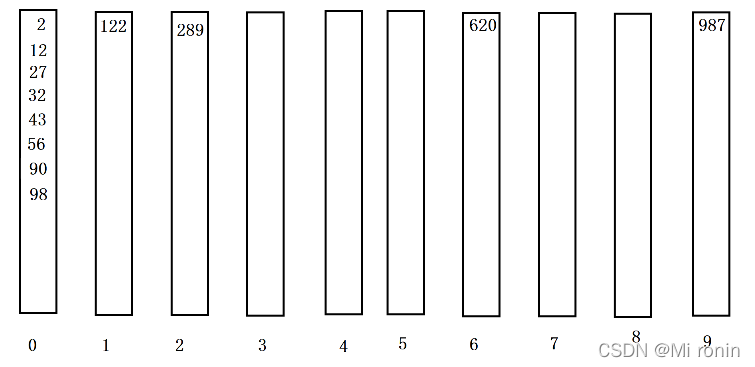
百位排序的最终结果：

2，12，27，32，43，56，90，98，122，289，620，987

（数据已完全有序）

2.3 代码实现

代码如下：

//获取数组中最大值的位数
int Get_figure(int* arr, int len)
{
	int max = 0;
	for (int i = 0; i < len; i++)
	{
		if (arr[i] > max)
		{
			max = arr[i];
		}
	}
	int count = 0;
	while (max != 0)
	{
		count++;
		max /= 10;
	}
	return count;
}
//这个函数告诉我传进来的参数n的，对应fin位是多少
//1234,2 -> 2    345,1 ->4    0078,3 -> 0     56789,4 -> 5
int Get_Num(int n, int fin)
{
	for (int i = 0; i < fin; i++)//这里代表需要n 先丢几位最低位
	{
		//n = n/10;
		n /= 10;
	}
	return n % 10;//此时获取剩余属于的最低位即可
}
//一趟桶排序    fin代表这一趟是根据哪个位进行排序（个，十，百......）   0->个位  1->十位...
void Radix(int* arr, int len, int fin)//时间复杂度O(n)
{
	//先将10个桶申请好
	int bucket[10][100] = { 0 };
	int num[10] = { 0 };  //num[1] 代表1号桶中有多少个有效值
	//将所有数据从左向右向对应的桶中存放
	for (int i = 0; i < len; i++)
	{
		int index = Get_Num(arr[i], fin);
		bucket[index][num[index]] = arr[i];
		num[index]++;
	}
	//按照0->9号桶的顺序，依次遵循先进先出的规则将所有值取出来
	int k = 0;
	for (int i = 0; i <= 9; i++)//0->9号桶依次取
	{
		for (int j = 0; j < num[i]; j++)//对应的桶内，从上到下依次取值
		{
			arr[k++] = bucket[i][j];//取出来的值 从前向后放到arr中
		}
	}
}
//基数排序（桶排序）  时间复杂度(d*n)（假设最大值的位数是d） 空间复杂度O（d*n） 稳定性：稳定
void RadixSort(int* arr, int len)
{
	//assert
	//1.首先需要知道 数据中最大值有多少位
	int count = Get_figure(arr, len);

	for (int i = 0; i < count; i++) //D
	{
		Radix(arr, len, i);
	}
}

2.4 性能分析

假设最大值的位数是d

• 时间复杂度：O （d*n）。
• 空间复杂度：O （d*n）。
• 稳定性：稳定。

到此这篇关于C语言深入探究选择排序与基数排序使用案例讲解的文章就介绍到这了,更多相关C语言排序内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！