关于Java float和double精度范围大小

目录

• Java float和double精度范围大小
• 一、小数的二进制转换(浮点数)
• 二、浮点数在计算机中的存储
• 三、指数位的偏移量与无符号表示
• 四、小结一下
• float和double的范围到底是多少
• 总结一下上面的

Java float和double精度范围大小

要想理解float和double的取值范围和计算精度，必须先了解小数是如何在计算机中存储的：

举个例子：78.375，是一个正小数。要在计算机中存储这个数，需要把它表示为浮点数的格式，先执行二进制转换：

一、小数的二进制转换(浮点数)

78.375的整数部分：

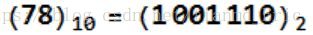
小数部分：

所以，78.375的二进制形式就是1001110.011

然后，使用二进制科学记数法，有

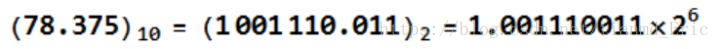
注意，转换后用二进制科学记数法表示的这个数，有底有指数有小数部分，这个就叫做浮点数

二、浮点数在计算机中的存储

在计算机中，保存这个数使用的是浮点表示法，分为三大部分：

• 第一部分用来存储符号位（sign），用来区分正负数，这里是0，表示正数
• 第二部分用来存储指数（exponent），这里的指数是十进制的6
• 第三部分用来存储小数（fraction），这里的小数部分是001110011

需要注意的是，指数也有正负之分，后面再讲。

如下图所示（图片来自维基百科）：

比如float类型是32位，是单精度浮点表示法：

• 符号位（sign）占用1位，用来表示正负数，
• 指数位（exponent）占用8位，用来表示指数，
• 小数位（fraction）占用23位，用来表示小数，不足位数补0。

而double类型是64位，是双精度浮点表示法：

• 符号位占用1位，指数位占用11位，小数位占用52位。

到这里其实已经可以隐隐看出：

• 指数位决定了大小范围，因为指数位能表示的数越大则能表示的数越大嘛！
• 而小数位决定了计算精度，因为小数位能表示的数越大，则能计算的精度越大咯！

可能还不够明白，举例子吧：

• float的小数位只有23位，即二进制的23位，能表示的最大的十进制数为2的23次方，即8388608，即十进制的7位，严格点，精度只能百分百保证十进制的6位运算。
• double的小数位有52位，对应十进制最大值为4 503 599 627 370 496，这个数有16位，所以计算精度只能百分百保证十进制的15位运算。

三、指数位的偏移量与无符号表示

需要注意的是指数可能是负数，也有可能是正数，即指数是有符号整数，而有符号整数的计算是比无符号整数麻烦的。所以为了减少不必要的麻烦，在实际存储指数的时候，需要把指数转换成无符号整数。那么怎么转换呢？

注意到float的指数部分是8位，则指数的取值范围是 -126到+127，为了消除负数带来的实际计算上的影响（比如比较大小，加减法等），可以在实际存储的时候，给指数做一个简单的映射，加上一个偏移量，比如float的指数偏移量为127，这样就不会有负数出现了。

比如

• 指数如果是6，则实际存储的是6+127=133，即把133转换为二进制之后再存储。
• 指数如果是-3，则实际存储的是-3+127=124，即把124转换为二进制之后再存储。

当我们需要计算实际代表的十进制数的时候，再把指数减去偏移量即可。

对应的double类型，存储的时候指数偏移量是1023。

四、小结一下

所以用float类型来保存十进制小数78.375的话，需要先转换成浮点数，得到符号位和指数和小数部分。

这个例子前面已经分析过，所以：

符号位是0，

指数位是6+127=133，二进制表示为10 000 101，

小数部分是001110011，不足部分请自动补0。

连起来用float表示，加粗部分是指数位，最左边是符号位0，代表正数：

0 10000101 001110011 00000 00000 0000

如果用double来保存。。。自己计算吧，太多0了。

float和double的范围到底是多少

Java中float占4个字节，32bit。计算范围公式为 ((-1)^S)* (2^(E-127))*(1.M) ,其中S占一位是符号位，E所占8bit是指数位，M占23位是尾数位。

这里一开始（1.M）部分一开始我一直没想明白为什么前面是1，突然有一天脑子开窍了，科学计数法表示的时候小数点前面就必须是1,所以规格化的时候小数点前面是1。

E占8位，所以大小是0-255，但是为了表示小数，指数部分需要可以是小数，对半一分，所以最后是E-127，也就是说指数部分为-127-128。

尾数部分没什么好说的，范围就是1-1.11……（23位全是1）

注意 ：尾数这里1.1111实际上是 十进制的1 + 二进制的0.1111， 什么意思呢, 举例说明会清楚一点：

1.1 ----> 1+1/2 = 1.5 = 2-1/2

1.11 -----> 1+1/2 +1/4 = 1.75 = 2-1/4

总结一下上面的

按道理最大值应该是(2^128)*(2-2^(-23))=2^129-2^105=6.81*10^38,但是一般书上说的都是3.40*10^38,那么问题又来了，为什么会大了2倍？

排除掉所有出书的人抄来抄去的行为导致所有的书都错了这个因素，那么剩下的只能是上面某个地方出了问题。首先，回到上面那个我加粗的规格化上去（我个人觉得完全可以用一般情况来代替这个词），仔细想想，假如所有的数都是上面那种规格化表示的时候：

第一：得到的数永远是（1.M）乘以一个数，指数部分是不会为0的，那么0怎么表示？

第二：无穷大和无穷小，还有NAN（not a number）又是怎么用这32bit表示出来的？我曾经想过的一个解释是，计算机里没有那个数就表示NAN嘛。。。以前还真觉得这个好有道理来着。但是计算机这个东西你只能当做一个工具，也就是说它不能无中生有，它只能处理我们给它的东西，所有无穷大无穷小还有NAN在计算机里肯定有一种表示方式。

所以，一定还有非规格化的表示，也就是所谓的特殊情况。

第一：当E是8个0的时候，此时就不是（1.M）而是（0.M）了，这个时候就可以表示出0了，当然还可以表示那些非常接近0的数。

第二：当E是8个1的时候，如果小数域全是0，表示的是无穷，其余的表示NAN。

由上可知，指数部分为（0-127）和（255-127）的时候表示的是两种特殊情况，所以E的范围应该是【-126，127】。最后，得出的结论是规格化的浮点数的表示范围是 正负(2^127)*(2-2^(-23))=2^128-2^104=3.40*10^38

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。