C语言编写汉诺塔游戏

目录
  • 汉诺塔的游戏规则：
    • 当A只有一个环的时候：
    • 当A只有两个环的时候：
    • 当A只有三个环的时候：
  • 思路：
    • 当n=1时：
    • 当n=2时：
    • 当n=3时：
    • 当n=4时：
  • 见代码
  • 运行截图总结

汉诺塔的游戏规则：

 

有三根金刚石柱子A、B、C，在A柱子上从下往上按照大小依次减小的顺序摞着64片黄金环。大梵天命令婆罗门把环从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在任何一个柱子上，小环上不能放大环，在三根柱子之间一次只能移动一个环。

即将A柱子上全部的环通过C柱子（C柱子作为中介）移动到B柱子上

当A只有一个环的时候：

A->B

当A只有两个环的时候：

A->C  A->B  C->B

当A只有三个环的时候：

A->B  A->C  B->C  A->B  C->A  C->B  A->B

思路：

  • 1、将 n-1个环先放到C柱子上
  • 2、将A柱子上的最后一个环移动到B柱子上
  • 3、将n-1个环从C柱子移动到B柱子上

当n=1时：

1、将0个环先放到C柱子上

2、将A柱子上的最后一个环移动到B柱子上：A->B

3、将0个环从C柱子移动到B柱子上

当n=2时：

1、将1个环先放到B柱子上：A->C

2、将A柱子上的最后一个环移动到B柱子上：A->B

3、将1个环从C柱子移动到B柱子上:C->B

当n=3时：

1、将2个环先放到C柱子上：使用递归将2个环放到C上，因为A柱子的最后一个环是最大的因此可以先不理会，递归重复当n=2时的步骤，不过是从将2个环从A放到B上改为将2个环从A放到C上了

2、将A柱子上的最后一个环移动到B柱子上：A->B

3、将2个环从C柱子移动到B柱子上:使用递归将2个环从C柱子移动到B柱子上，此时B柱子上已经有了最大的一个环因此可以不用再理会了，递归重复当n=2的步骤，不过是从将2个环从A放到B上改为将2个环从C放到B上了

当n=4时：

1、将3个环先放到C柱子上：递归重复n=3的步骤，不过是从将3个环从A放到B上改为将3个环从A放到C上了

2、将A柱子上的最后一个环移动到B柱子上：A->B

3、将3个环从C柱子移动到B柱子上:递归重复当n=3的步骤，不过是从将3个环从A放到B上改为将3个环从C放到B上了

见代码

 #include <stdio.h>
void hanoi(int num, char sou, char tar, char aux) {
    //统计移动次数
    static int i = 1;
    //如果圆盘数量仅有 1 个，则直接从起始柱移动到目标柱
    if (num == 1) {
        printf("第%2d次:从 %c 移动至 %c\n", i, sou, tar);
        i++;
    }
    else {
        //递归调用 hanoi() 函数，将 num-1 个圆盘从起始柱移动到辅助柱上
        hanoi(num - 1, sou, aux, tar);
        //将起始柱上剩余的最后一个大圆盘移动到目标柱上
        printf("第%2d次:从 %c 移动至 %c\n", i, sou, tar);
        i++;
        //递归调用 hanoi() 函数，将辅助柱上的 num-1 圆盘移动到目标柱上
        hanoi(num - 1, aux, tar, sou);
    }
}
int main()
{
    int n = 0;
    scanf("%d", &n);
    //起始柱、目标柱、辅助柱分别用 A、B、C 表示
    hanoi(n, 'A', 'B', 'C');
    return 0;
}

运行截图总结

 

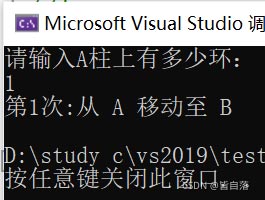
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • C语言编程递归算法实现汉诺塔

    C语言编程递归算法实现汉诺塔

    汉诺塔 法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针.印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔.不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面.僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔.庙宇和众生也都将同归于尽. 这个传说挺有意思的,这个传说

  • C语言汉诺塔的简单了解

    C语言汉诺塔的简单了解

    汉诺塔详解 以4层为例 以下为我的拙见,还希望大佬雅正 要把汉诺塔移动到c 需要把1,2,3层移到b 把4移动到c 在吧123移动到b 但是一次只能动一块 所以我们目前要做的就是把上面三块移动到b 那就需要把1 2移动到c 由此我们可以推出要把1,2移动到c,只需要把1移动到b 这里我们发现有很多重复的自相似动作 我们就可以设计递归 递归需要1,递归体 2 出口. 递归体 移动n-1个盘子和1个盘子和n个盘子过程都是相似的 但是每次放入的杆子不一样. 出口 n=1时只剩一个盘子,直接移动到c即可

  • C语言实现汉诺塔游戏

    C语言实现汉诺塔游戏

    操作就是:A B 号码A的塔顶一层放在号码B的塔顶.如1(空格) 3 回车. 话说有人能把我这C的代码添加到QT界面框架上去么?  代码写的不好 ,维护性不够,只能玩8层的,写完以后发现很难拓展,软件工程,设计模式有待提高.... 里面提示输入等级的装B用了,没有实现,大家随便输入个个位数就可以玩了. stackfunc.c #include"STACK.h" #include<stdio.h> extern ceng CENG[SIZE]; //数据入栈 void pus

  • c语言 汉诺塔算法代码

    复制代码 代码如下: #include<stdio.h> void move(char a,char b) {     printf("%c->%c\n",a,b); } void han(int n,char a,char b,char c) {     if(n>0)     {         han(n-1,a,c,b);         move(a,b);         han(n-1,c,b,a);     } } int main() {   

  • C语言编写汉诺塔游戏

    C语言编写汉诺塔游戏

    目录 汉诺塔的游戏规则: 当A只有一个环的时候: 当A只有两个环的时候: 当A只有三个环的时候: 思路: 当n=1时: 当n=2时: 当n=3时: 当n=4时: 见代码 运行截图总结 汉诺塔的游戏规则:   有三根金刚石柱子A.B.C,在A柱子上从下往上按照大小依次减小的顺序摞着64片黄金环.大梵天命令婆罗门把环从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在任何一个柱子上,小环上不能放大环,在三根柱子之间一次只能移动一个环. 即将A柱子上全部的环通过C柱子(C柱子作为中介)移动到B柱子

  • c# 实现汉诺塔游戏

    汉诺塔游戏一旦掌握了规律,其实是有点单调和无聊的,不过却是学习递归的一个绝佳例子,想当初学习老谭C的时候,就卡在这儿好长时间. 对初学编程的人来说,递归本身就不易理解,如果使用C语言没有好的调试环境就更难去理解了.在这方面,VS调试输出是真方便,一目了然. 但要想理解递归求解汉诺塔,还是得先玩一玩游戏本身,有点感受.另外,设计一下这个游戏也可以加深对它的理解,同时还可以对数据结构中的栈有一个简单的认识. 因为汉诺塔的游戏规则本身就是一个栈,只能从平台最上面取走碟子,然后放在另一个平台最上面,这明

  • python求解汉诺塔游戏

    本文实例为大家分享了python求解汉诺塔游戏的具体代码,供大家参考,具体内容如下 一.问题定义 百度百科定义:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.据说大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照从小到大顺序摞着64片黄金圆盘.大梵天命令婆罗门借助其中一根柱子,把64片黄金圆盘重新摆放到第三个根柱子上.并且规定,在小黄金圆盘上不能放大的黄金圆盘,在三根柱子之间一次只能移动一个圆盘. 例如,如果黄金圆盘只有3片,则为了满足游戏规则,那么必须按照如下图所示的

  • python 实现汉诺塔游戏

    一.汉诺塔问题 1. 问题来源 问题源于印度的一个古老传说,大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘. 2. 问题阐述 塔内有三个座A.B.C,A座上有64个盘子,盘子从上到下逐渐变大,最下面的盘子最大.目前要把A座的64个盘子从A座移到C座,并且每次只能移动一个盘子,移动过程中三个座保持大盘子在下,小盘子在上,

  • 利用python实现汉诺塔游戏

    利用python实现汉诺塔游戏

    本文实例为大家分享了python实现汉诺塔游戏的具体代码,供大家参考,具体内容如下 一.汉诺塔 汉诺塔问题是一个经典的递归问题,对于这个问题,我们可以把它简单的去看成是如何用n-1去表示n. 在A,B,C三个柱子上,我们先假设A柱上只有两个盘子,那么很简单,只需要把最上面的那个盘子移到B柱上,再把A柱上最下面的盘子移到C柱上,最后把B柱的盘子移到C柱就可以了. 假设我们有n个盘子,那么可以把最下面的盘子看成是第n个盘子,而我们要做的是把上面n-1个盘子移到B柱上,再把第n个盘子移到C柱.我们可以

  • Java递归来实现汉诺塔游戏,注释详细

    Java递归来实现汉诺塔游戏,注释详细

    我们很容易能想到,可以用递归来实现汉诺塔游戏.因为要将n(n>1)个盘子从"源"柱子移到"目标"柱子,我们要先把n-1个盘子从"源"柱子移到"辅助"柱子上,然后把最底下那一个盘子移到目标柱子上,最后把"辅助柱"上的n-1个盘子移动到目标柱子上.n==1时直接移到目标柱上,也是递归的出口. 有了以上思路的铺垫,就可以开始实现代码了. public class HanoiDemo { public sta

  • C语言实现汉诺塔(图文详解)

    C语言实现汉诺塔(图文详解)

    目录 思路: 当n=1时: 当n=2时: 当n=3时: 当n=4时: 见代码 运行截图 总结 汉诺塔的游戏规则: 有三根金刚石柱子A.B.C,在A柱子上从下往上按照大小依次减小的顺序摞着64片黄金环.大梵天命令婆罗门把环从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在任何一个柱子上,小环上不能放大环,在三根柱子之间一次只能移动一个环. 即将A柱子上全部的环通过中间柱子B(B柱子作为中介)移动到C柱子上 当A只有一个环的时候: A->C 当A只有两个环的时候: A->B A->C

  • Go语言实现汉诺塔算法

    hano.go package main import ( "bufio" "fmt" "os" "strconv" ) func main() { fmt.Print("输入要移动的盘子数:") reader := bufio.NewReader(os.Stdin) lool: data, _, _ := reader.ReadLine() n, err := strconv.Atoi(string(da

  • C语言递归：汉诺塔问题分析

    目录 问题背景 游戏体验 汉诺塔移动次数规律 移动过程的深层解读 汉诺塔问题的三步过程归纳 图解: 发现: 代码实现1 仅打印移动次数 代码实现2 打印移动的具体过程 补充 问题背景 汉诺塔问题源自印度一个古老的传说,印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱,其中的一根柱子上按照从小到大的顺序摞着 64 个黄金圆盘.梵天命令一个叫婆罗门的门徒将所有的圆盘移动到另一个柱子上,移动过程中必须遵守以下规则: 每次只能移动柱子最顶端的一个圆盘:每个柱子上,小圆盘永远要位于大圆盘之上: 游戏

随机推荐