使用Python实现正态分布、正态分布采样

多元正态分布(多元高斯分布)

直接从多元正态分布讲起。多元正态分布公式如下：

这就是多元正态分布的定义，均值好理解，就是高斯分布的概率分布值最大的位置，进行采样时也就是采样的中心点。而协方差矩阵在多维上形式较多。

协方差矩阵

一般来说，协方差矩阵有三种形式，分别称为球形、对角和全协方差。以二元为例：

为了方便展示不同协方差矩阵的效果，我们以二维为例。(书上截的图，凑活着看吧，是在不想画图了)

其实从这个图上可以很好的看出，协方差矩阵对正态分布的影响，也就很好明白了这三个协方差矩阵是哪里来的名字了。可以看出，球形协方差矩阵，会产生圆形(二维)或者球形(三维)的等高线，对角协方差矩阵和全协方差矩阵，会产生椭圆形的等高线。更一般地，在一个D维空间中，球形协方差矩阵，会产生一个D维球面等高线；对角协方差矩阵，会产生一个坐标轴对其的椭球型等高线；全协方差矩阵，会在任意位置产生一个坐标轴对其的椭球型等高线。

当协方差矩阵是球形的或者是对角的，单独的变量之间是独立的

协方差分解

时间不足，具体解释以后再补

下面是协方差分解的原理图

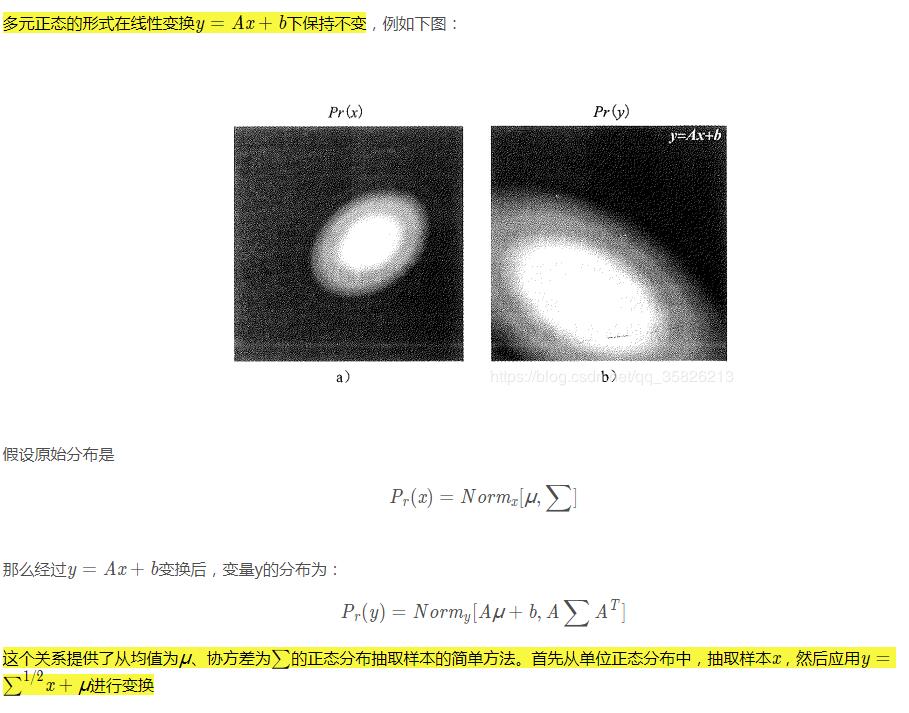
变量的线性变换(正态分布采样原理)

python实现

多元正态分布在python的numpy库中有很方便一个函数：

np.random.multivariate_normal(mean=mean, cov=conv, size=N)

这个函数中，mean代表均值，是在每个维度中的均值。cov代表协方差矩阵，就像上面讲的那种形式，协方差矩阵值的大小将决定采样范围的大小。size代表需要采样生成的点数，此时输出大小为（N*D）的坐标矩阵。

另外，其他参数包括：check_valid，这个参数用于决定当cov即协方差矩阵不是半正定矩阵时程序的处理方式，它一共有三个值：warn，raise以及ignore。当使用warn作为传入的参数时，如果cov不是半正定的程序会输出警告但仍旧会得到结果；当使用raise作为传入的参数时，如果cov不是半正定的程序会报错且不会计算出结果；当使用ignore时忽略这个问题即无论cov是否为半正定的都会计算出结果

tol：检查协方差矩阵奇异值时的公差，float类型。

下面是一个小demo

import numpy as np
import matplotlib.pyplot as plt

mean = np.array([2,1])    # 均值
conv = np.array([[0.5, 0.0],  # 协方差矩阵
     [0.0, 0.5]])
axis = np.random.multivariate_normal(mean=mean, cov=conv, size=200)
x, y = np.random.multivariate_normal(mean=mean, cov=conv, size=1000).T

# print(axis[:])

plt.plot(axis[:, 0], axis[:, 1], 'ro')
plt.show()
plt.plot(x, y, 'ro')
plt.show()

注意，单独取出每个坐标轴的坐标数组时，需要在最后加上.T，否则会报错 效果展示：

协方差值的大小对采样的影响：

mean = np.array([2,1])    # 均值
conv = np.array([[0.5, 0.0],  # 协方差矩阵
     [0.0, 0.5]])

conv2 = np.array([[10, 0.0],  # 协方差矩阵
     [0.0, 10]])
axis = np.random.multivariate_normal(mean=mean, cov=conv, size=200)
x, y = np.random.multivariate_normal(mean=mean, cov=conv2, size=200).T

# print(axis[:])

plt.plot(axis[:, 0], axis[:, 1], 'ro')
plt.show()
plt.plot(x, y, 'ro')
plt.show()

效果如下：

这里没有设定随机种子店，每次随机数会有所不同。

以上这篇使用Python实现正态分布、正态分布采样就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • 使用python绘制3维正态分布图的方法

    今天使用python画了几个好玩的3D展示图,现在分享给大家. 先贴上图片 使用的python工具包为: from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D 在贴代码之前,有必要从整体上了解这些图是如何画出来的.可以把上面每一个3D图片理解成一个长方体.输入数据是三维的,x轴y轴和z轴.在第三个图片里面有x.y和z坐标的标识.在第三张图片中,我们可以理解为,

  • 在python中画正态分布图像的实例

    1.正态分布简介 正态分布(normal distribtution)又叫做高斯分布(Gaussian distribution),是一个非常重要也非常常见的连续概率分布.正态分布大家也都非常熟悉,下面做一些简单的介绍. 假设随机变量XX服从一个位置参数为μμ.尺度参数为σσ的正态分布,则可以记为: 而概率密度函数为 2.在python中画正态分布直方图 先直接上代码 import numpy as np import matplotlib.mlab as mlab import matplot

  • Python求正态分布曲线下面积实例

    正态分布应用最广泛的连续概率分布,其特征是"钟"形曲线.这种分布的概率密度函数为: 其中,μ为均值,σ为标准差. 求正态分布曲线下面积有3σ原则: 正态曲线下,横轴区间(μ-σ,μ+σ)内的面积为68.268949%,横轴区间(μ-1.96σ,μ+1.96σ)内的面积为95.449974%,横轴区间(μ-2.58σ,μ+2.58σ)内的面积为99.730020%. 求任意区间内曲线下的面积,通常可以引用scipy包中的相关函数 norm函数生成一个给定均值和标准差的正态分布,cdf(x

  • Python使用numpy产生正态分布随机数的向量或矩阵操作示例

    Python使用numpy产生正态分布随机数的向量或矩阵操作示例

    本文实例讲述了Python使用numpy产生正态分布随机数的向量或矩阵操作.分享给大家供大家参考,具体如下: 简单来说,正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学.物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力.一般的正态分布可以通过标准正态分布配合数学期望向量和协方差矩阵得到.如下代码,可以得到满足一维和二维正态分布的样本. 示例1(一维正态分布): # coding=utf-8 '''

  • Python求解正态分布置信区间教程

    正态分布和置信区间 正态分布(Normal Distribution)又叫高斯分布,是一种非常重要的概率分布.其概率密度函数的数学表达如下: 置信区间是对该区间能包含未知参数的可置信的程度的描述. 使用SciPy求解置信区间 import numpy as np import matplotlib.pyplot as plt from scipy import stats N = 10000 x = np.random.normal(0, 1, N) # ddof取值为1是因为在统计学中样本的标

  • Python数据可视化实现正态分布（高斯分布）

    正态分布(Normal distribution)又成为高斯分布(Gaussian distribution) 若随机变量X服从一个数学期望为.标准方差为的高斯分布,记为: 则其概率密度函数为: 正态分布的期望值决定了其位置,其标准差决定了分布的幅度.因其曲线呈钟形,因此人们又经常称之为钟形曲线.我们通常所说的标准正态分布是的正态分布: 概率密度函数 代码实现: # Python实现正态分布 # 绘制正态分布概率密度函数 u = 0 # 均值μ u01 = -2 sig = math.sqrt(

  • Python数据可视化正态分布简单分析及实现代码

    Python数据可视化正态分布简单分析及实现代码

    Python说来简单也简单,但是也不简单,尤其是再跟高数结合起来的时候... 正态分布(Normaldistribution),也称"常态分布",又名高斯分布(Gaussiandistribution),最早由A.棣莫弗在求二项分布的渐近公式中得到.C.F.高斯在研究测量误差时从另一个角度导出了它.P.S.拉普拉斯和高斯研究了它的性质.是一个在数学.物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力. 正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人

  • 浅析Python中的随机采样和概率分布

    目录 1. random.choice 2. random.choices(有放回) 3. numpy.sample(无放回) 4.rng.choices 和 rng.sample 5. numpy.random.choices 参考文献  Python(包括其包Numpy)中包含了了许多概率算法,包括基础的随机采样以及许多经典的概率分布生成.我们这个系列介绍几个在机器学习中常用的概率函数.先来看最基础的功能--随机采样. 1. random.choice 如果我们只需要从序列里采一个样本(所有

  • 使用Python实现正态分布、正态分布采样

    多元正态分布(多元高斯分布) 直接从多元正态分布讲起.多元正态分布公式如下: 这就是多元正态分布的定义,均值好理解,就是高斯分布的概率分布值最大的位置,进行采样时也就是采样的中心点.而协方差矩阵在多维上形式较多. 协方差矩阵 一般来说,协方差矩阵有三种形式,分别称为球形.对角和全协方差.以二元为例: 为了方便展示不同协方差矩阵的效果,我们以二维为例.(书上截的图,凑活着看吧,是在不想画图了) 其实从这个图上可以很好的看出,协方差矩阵对正态分布的影响,也就很好明白了这三个协方差矩阵是哪里来的名字了

  • Python实现从概率分布中随机采样

    Python实现从概率分布中随机采样

    目录 1. 二项(binomial)/伯努利(Bernoulli)分布 2. 多项(multinomial)分布 3.均匀(uniform)分布 4. 狄利克雷(Dirichlet)分布 参考文献 在上一篇博文<Python中的随机采样和概率分布(一)>中,我们介绍了Python中最简单的随机采样函数.接下来我们更进一步,来看看如何从一个概率分布中采样,我们以几个机器学习中最常用的概率分布为例. 1. 二项(binomial)/伯努利(Bernoulli)分布 1.1 概率质量函数(pmf)

  • Python随机采样及概率分布(二)

    Python随机采样及概率分布(二)

    目录 1. 二项(binomial)/伯努利(Bernoulli)分布 1.1 概率质量函数(pmf) 1.2 函数原型 1.3 使用样例 2. 多项(multinomial)分布 2.1 概率质量函数(pmf) 2.2 函数原型 2.3 使用样例 3.均匀(uniform)分布 3.1 概率密度函数(pdf) 3.2 函数原型 3.3 使用样例 4. 狄利克雷(Dirichlet)分布 4.1 概率密度函数(pdf) 4.2 函数原型 4.3 使用样例 前言: 之前的<Python中的随机采样

  • Python编程产生非均匀随机数的几种方法代码分享

    Python编程产生非均匀随机数的几种方法代码分享

    1.反变换法 设需产生分布函数为F(x)的连续随机数X.若已有[0,1]区间均匀分布随机数R,则产生X的反变换公式为: F(x)=r, 即x=F-1(r) 反函数存在条件:如果函数y=f(x)是定义域D上的单调函数,那么f(x)一定有反函数存在,且反函数一定是单调的.分布函数F(x)为是一个单调递增函数,所以其反函数存在.从直观意义上理解,因为r一一对应着x,而在[0,1]均匀分布随机数R≤r的概率P(R≤r)=r. 因此,连续随机数X≤x的概率P(X≤x)=P(R≤r)=r=F(x) 即X的分

  • python编程通过蒙特卡洛法计算定积分详解

    想当初,考研的时候要是知道有这么个好东西,计算定积分...开玩笑,那时候计算定积分根本没有这么简单的.但这确实给我打开了一种思路,用编程语言去解决更多更复杂的数学问题.下面进入正题. 如上图所示,计算区间[a b]上f(x)的积分即求曲线与X轴围成红色区域的面积.下面使用蒙特卡洛法计算区间[2 3]上的定积分:∫(x2+4*x*sin(x))dx # -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt

  • Python实现比较扑克牌大小程序代码示例

    是Udacity课程的第一个项目. 先从宏观把握一下思路,目的是做一个比较德州扑克大小的问题 首先,先抽象出一个处理的函数,它根据返回值的大小给出结果. 之后我们在定义如何比较两个或者多个手牌的大小,为方便比较大小,我们先对5张牌进行预处理,将其按照降序排序,如下: def card_ranks(hand): ranks = ['--23456789TJQKA'.INDEX(r) for r, s in hand] ranks.sort(reverse=True) return ranks 然后

  • 浅谈python可视化包Bokeh

    本文研究的主要是python可视化包Bokeh的相关内容,具体如下. 问题:需要把pandas的数据绘图并通过网页显示,matplotlib需要先保存图像,不合适. 解决:在网上搜了一下,找到一篇介绍文章 python可视化工具概述,其中介绍了几个python包,总结如下: Pandas对于简单绘图,可以随手用,但你需要学习定制matplotlib. Seaborn可以支持更多复杂的可视化方式,但仍然需要matplotlib知识,上色功能是个亮点. ggplot有很多功能,但还需要发展. bok

随机推荐