Java数据结构之图的路径查找算法详解
目录
- 前言
- 算法详解
- 实现
- API设计
- 代码实现
前言
在实际生活中,地图是我们经常使用的一种工具,通常我们会用它进行导航,输入一个出发城市,输入一个目的地
城市,就可以把路线规划好,而在规划好的这个路线上,会路过很多中间的城市。这类问题翻译成专业问题就是:
从s顶点到v顶点是否存在一条路径?如果存在,请找出这条路径。
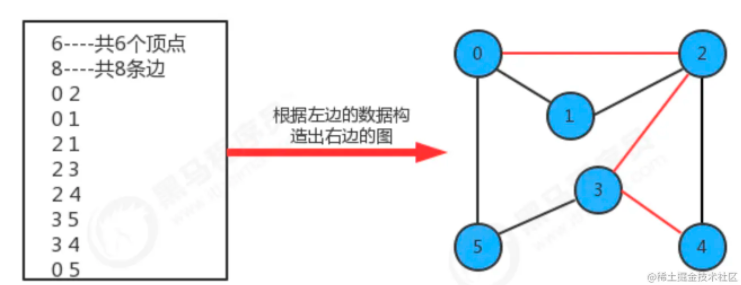
例如在上图上查找顶点0到顶点4的路径用红色标识出来,那么我们可以把该路径表示为 0-2-3-4。
如果对图的前置知识不了解,请查看系列文章:
【数据结构与算法】图的基础概念和数据模型
【数据结构与算法】图的两种搜索算法
算法详解
我们实现路径查找,最基本的操作还是得遍历并搜索图,所以,我们的实现暂且基于深度优先搜索来完成。其搜索
的过程是比较简单的。我们添加了edgeTo[]整型数组,这个整型数组会记录从每个顶点回到起点s的路径。
如果我们把顶点设定为0,那么它的搜索可以表示为下图:
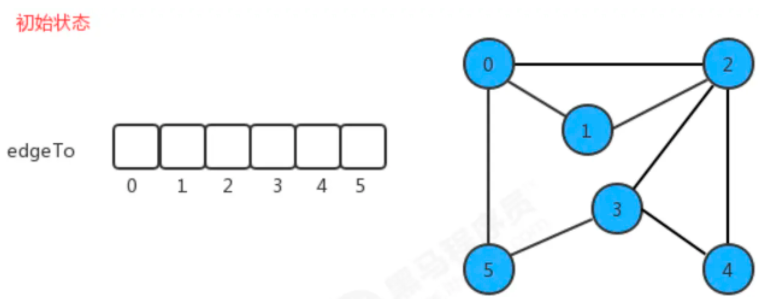
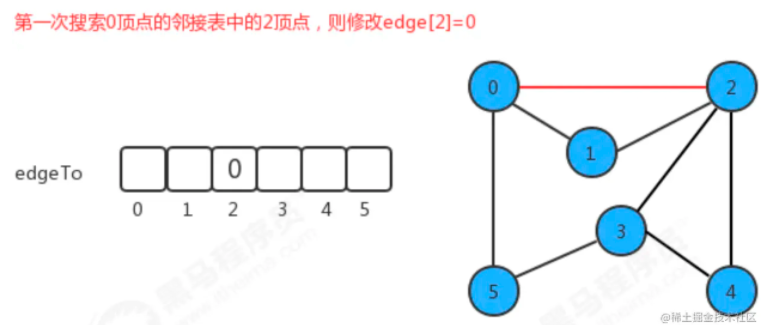
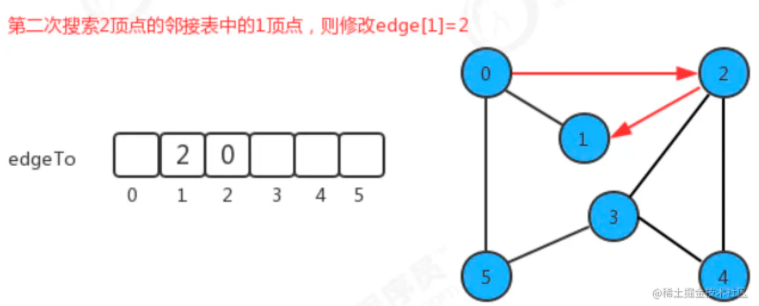

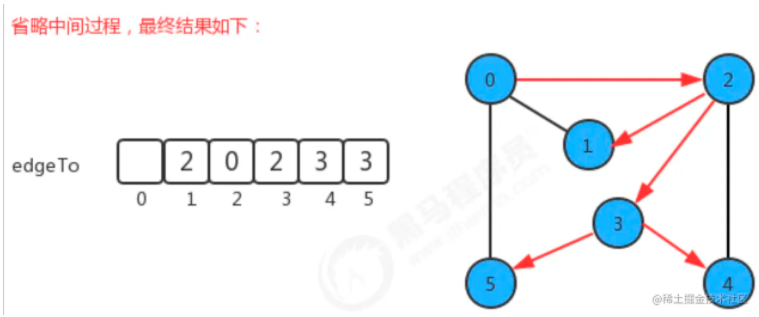
总结来说,就是edgeTo数组的下标表示当前顶点,内容存放上一个节点的数据,根据最终edgeTo的结果,我们很容易能够找到从起点0到任意顶点的路径。
实现
API设计
| 类名 | DepthFirstPaths |
|---|---|
| 成员变量 | 1.private boolean[] marked: 索引代表顶点,值表示当前顶点是否已经被搜索2.private int s:起点3.private int[] edgeTo:索引代表顶点,值代表从起点s到当前顶点路径上的最后一个顶点 |
| 构造方法 | DepthFirstPaths(Graph G,int s):构造深度优先搜索对象,使用深度优先搜索找出G图中起点为s的所有路径 |
| 成员方法 | 1.private void dfs(Graph G, int v):使用深度优先搜索找出G图中v顶点的所有相邻顶点2.public boolean hasPathTo(int v):判断v顶点与s顶点是否存在路径3.public Stack pathTo(int v):找出从起点s到顶点v的路径(就是该路径经过的顶点) |
代码实现
/**
* 路径查找
*
* @author alvin
* @date 2022/10/31
* @since 1.0
**/
public class DepthFirstPaths {
//索引代表顶点,值表示当前顶点是否已经被搜索
private boolean[] marked;
//起点
private int s;
//索引代表顶点,值代表从起点s到当前顶点路径上的最后一个顶点
private int[] edgeTo;
//构造深度优先搜索对象,使用深度优先搜索找出G图中起点为s的所有路径
public DepthFirstPaths(Graph G, int s){
//初始化marked数组
this.marked = new boolean[G.V()];
//初始化起点
this.s = s;
//初始化edgeTo数组
this.edgeTo = new int[G.V()];
dfs(G,s);
}
//使用深度优先搜索找出G图中v顶点的所有相邻顶点
private void dfs(Graph G, int v){
//把v表示为已搜索
marked[v] = true;
//遍历顶点v的邻接表,拿到每一个相邻的顶点,继续递归搜索
for (Integer w : G.adj(v)) {
//如果顶点w没有被搜索,则继续递归搜索
if (!marked[w]){
edgeTo[w] = v;//到达顶点w的路径上的最后一个顶点是v
dfs(G,w);
}
}
}
//判断w顶点与s顶点是否存在路径
public boolean hasPathTo(int v){
return marked[v];
}
//找出从起点s到顶点v的路径(就是该路径经过的顶点)
public Stack<Integer> pathTo(int v){
if (!hasPathTo(v)){
return null;
}
//创建栈对象,保存路径中的所有顶点
Stack<Integer> path = new Stack<>();
//通过循环,从顶点v开始,一直往前找,到找到起点为止
for (int x = v; x!=s;x = edgeTo[x]){
path.push(x);
}
//把起点s放到栈中
path.push(s);
return path;
}
}
测试:
public class DepthFirstPathsTest {
@Test
public void test() {
//城市数量
int totalNumber = 20;
Graph G = new Graph(totalNumber);
//添加城市的交通路线
G.addEdge(0,1);
G.addEdge(6,9);
G.addEdge(1,8);
G.addEdge(1,12);
G.addEdge(8,12);
G.addEdge(6,10);
G.addEdge(4,8);
DepthFirstPaths depthFirstPaths = new DepthFirstPaths(G, 0);
Stack<Integer> path = depthFirstPaths.pathTo(12);
StringBuilder sb = new StringBuilder();
//遍历栈对象
for (Integer v : path) {
sb.append(v+"->");
}
sb.deleteCharAt(sb.length()-1);
sb.deleteCharAt(sb.length()-1);
System.out.println(sb);
}
}
到此这篇关于Java数据结构之图的路径查找算法详解的文章就介绍到这了,更多相关Java图路径查找内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!
赞 (0)

