Python实现简单遗传算法(SGA)

本文用Python3完整实现了简单遗传算法(SGA)

Simple Genetic Alogrithm是模拟生物进化过程而提出的一种优化算法。SGA采用随机导向搜索全局最优解或者说近似全局最优解。传统的爬山算法(例如梯度下降，牛顿法)一次只优化一个解，并且对于多峰的目标函数很容易陷入局部最优解，而SGA算法一次优化一个种群(即一次优化多个解)，SGA比传统的爬山算法更容易收敛到全局最优解或者近似全局最优解。
SGA基本流程如下:

1、对问题的解进行二进制编码。编码涉及精度的问题，在本例中精度delta=0.0001,根据决策变量的上下界确定对应此决策变量的染色体基因的长度（m）。假设一个决策变量x0上界为upper,下界为lower,则精度delta = (upper-lower)/2^m-1。如果已知决策变量边界和编码精度，那么可以用下面的公式确定编码决策变量x0所对应的染色体长度：

2^(length-1)<(upper-lower)/delta<=2^length-1

2、对染色体解码得到表现形:

解码后得到10进制的值；decoded = lower + binary2demical(chromosome)*delta。其中binary2demical为二进制转10进制的函数，在代码中有实现，chromosome是编码后的染色体。

3、确定初始种群,初始种群随机生成

4、根据解码函数得到初始种群的10进制表现型的值

5、确定适应度函数，对于求最大值最小值问题，一般适应度函数就是目标函数。根据适应度函数确定每个个体的适应度值Fi=FitnessFunction(individual);然后确定每个个体被选择的概率Pi=Fi/sum(Fi),sum(Fi)代表所有个体适应度之和。

6、根据轮盘赌选择算子，选取适应度较大的个体。一次选取一个个体，选取n次,得到新的种群population

7、确定交叉概率Pc,对上一步得到的种群进行单点交叉。每次交叉点的位置随机。

8、确定变异概率Pm,假设种群大小为10，每个个体染色体编码长度为33，则一共有330个基因位，则变异的基因位数是330*Pm。接下来，要确定是那个染色体中哪个位置的基因发生了变异。将330按照10进制序号进行编码即从0,1,2,.......229。随机从330个数中选择330*Pm个数，假设其中一个数时154，chromosomeIndex = 154/33 =4,
geneIndex = 154%33 = 22。由此确定了第154号位置的基因位于第4个染色体的第22个位置上，将此位置的基因值置反完成基本位变异操作。

9、以上步骤完成了一次迭代的所有操作。接下就是评估的过程。对变异后得到的最终的种群进行解码，利用解码值求得每个个体的适应度值，将最大的适应度值保存下来，对应的解码后的决策变量的值也保存下来。

10、根据迭代次数，假设是500次，重复执行1-9的步骤，最终得到是一个500个数值的最优适应度取值的数组以及一个500*n的决策变量取值数组（假设有n个决策变量）。从500个值中找到最优的一个（最大或者最小，根据定义的适应度函数来选择）以及对应的决策变量的取值。
对于以上流程不是很清楚的地方，在代码中有详细的注释。也可以自行查找资料补充理论。本文重点是实现
本代码实现的问题是: maxf(x1,x2) = 21.5+x1*sin(4*pi*x1)+x2*sin(20*pi*x2)
                         s.t. -3.0<=x1<=12.1
4.1<=x2<=5.8

初始种群的编码结果如下图所示:

初始种群的解码结果如下图所示:

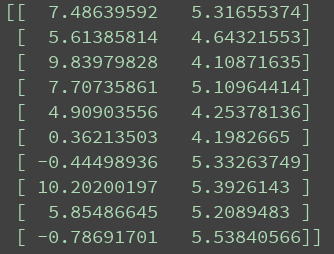
适应度值如图所示:

轮盘赌选择后的种群如图所示；

单点交叉后的种群如图所示:

基本位变异后的种群如图所示；

最终结果如下图所示；

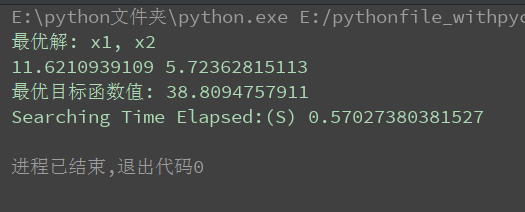
源代码如下；

# !/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: wsw
# 简单实现SGA算法
import numpy as np
from scipy.optimize import fsolve, basinhopping
import random
import timeit 

# 根据解的精度确定染色体(chromosome)的长度
# 需要根据决策变量的上下边界来确定
def getEncodedLength(delta=0.0001, boundarylist=[]):
 # 每个变量的编码长度
 lengths = []
 for i in boundarylist:
  lower = i[0]
  upper = i[1]
  # lamnda 代表匿名函数f(x)=0,50代表搜索的初始解
  res = fsolve(lambda x: ((upper - lower) * 1 / delta) - 2 ** x - 1, 50)
  length = int(np.floor(res[0]))
  lengths.append(length)
 return lengths
 pass 

# 随机生成初始编码种群
def getIntialPopulation(encodelength, populationSize):
 # 随机化初始种群为0
 chromosomes = np.zeros((populationSize, sum(encodelength)), dtype=np.uint8)
 for i in range(populationSize):
  chromosomes[i, :] = np.random.randint(0, 2, sum(encodelength))
 # print('chromosomes shape:', chromosomes.shape)
 return chromosomes 

# 染色体解码得到表现型的解
def decodedChromosome(encodelength, chromosomes, boundarylist, delta=0.0001):
 populations = chromosomes.shape[0]
 variables = len(encodelength)
 decodedvalues = np.zeros((populations, variables))
 for k, chromosome in enumerate(chromosomes):
  chromosome = chromosome.tolist()
  start = 0
  for index, length in enumerate(encodelength):
   # 将一个染色体进行拆分，得到染色体片段
   power = length - 1
   # 解码得到的10进制数字
   demical = 0
   for i in range(start, length + start):
    demical += chromosome[i] * (2 ** power)
    power -= 1
   lower = boundarylist[index][0]
   upper = boundarylist[index][1]
   decodedvalue = lower + demical * (upper - lower) / (2 ** length - 1)
   decodedvalues[k, index] = decodedvalue
   # 开始去下一段染色体的编码
   start = length
 return decodedvalues 

# 得到个体的适应度值及每个个体被选择的累积概率
def getFitnessValue(func, chromosomesdecoded):
 # 得到种群规模和决策变量的个数
 population, nums = chromosomesdecoded.shape
 # 初始化种群的适应度值为0
 fitnessvalues = np.zeros((population, 1))
 # 计算适应度值
 for i in range(population):
  fitnessvalues[i, 0] = func(chromosomesdecoded[i, :])
 # 计算每个染色体被选择的概率
 probability = fitnessvalues / np.sum(fitnessvalues)
 # 得到每个染色体被选中的累积概率
 cum_probability = np.cumsum(probability)
 return fitnessvalues, cum_probability 

# 新种群选择
def selectNewPopulation(chromosomes, cum_probability):
 m, n = chromosomes.shape
 newpopulation = np.zeros((m, n), dtype=np.uint8)
 # 随机产生M个概率值
 randoms = np.random.rand(m)
 for i, randoma in enumerate(randoms):
  logical = cum_probability >= randoma
  index = np.where(logical == 1)
  # index是tuple,tuple中元素是ndarray
  newpopulation[i, :] = chromosomes[index[0][0], :]
 return newpopulation
 pass 

# 新种群交叉
def crossover(population, Pc=0.8):
 """
 :param population: 新种群
 :param Pc: 交叉概率默认是0.8
 :return: 交叉后得到的新种群
 """
 # 根据交叉概率计算需要进行交叉的个体个数
 m, n = population.shape
 numbers = np.uint8(m * Pc)
 # 确保进行交叉的染色体个数是偶数个
 if numbers % 2 != 0:
  numbers += 1
 # 交叉后得到的新种群
 updatepopulation = np.zeros((m, n), dtype=np.uint8)
 # 产生随机索引
 index = random.sample(range(m), numbers)
 # 不进行交叉的染色体进行复制
 for i in range(m):
  if not index.__contains__(i):
   updatepopulation[i, :] = population[i, :]
 # crossover
 while len(index) > 0:
  a = index.pop()
  b = index.pop()
  # 随机产生一个交叉点
  crossoverPoint = random.sample(range(1, n), 1)
  crossoverPoint = crossoverPoint[0]
  # one-single-point crossover
  updatepopulation[a, 0:crossoverPoint] = population[a, 0:crossoverPoint]
  updatepopulation[a, crossoverPoint:] = population[b, crossoverPoint:]
  updatepopulation[b, 0:crossoverPoint] = population[b, 0:crossoverPoint]
  updatepopulation[b, crossoverPoint:] = population[a, crossoverPoint:]
 return updatepopulation
 pass 

# 染色体变异
def mutation(population, Pm=0.01):
 """ 

 :param population: 经交叉后得到的种群
 :param Pm: 变异概率默认是0.01
 :return: 经变异操作后的新种群
 """
 updatepopulation = np.copy(population)
 m, n = population.shape
 # 计算需要变异的基因个数
 gene_num = np.uint8(m * n * Pm)
 # 将所有的基因按照序号进行10进制编码，则共有m*n个基因
 # 随机抽取gene_num个基因进行基本位变异
 mutationGeneIndex = random.sample(range(0, m * n), gene_num)
 # 确定每个将要变异的基因在整个染色体中的基因座(即基因的具体位置)
 for gene in mutationGeneIndex:
  # 确定变异基因位于第几个染色体
  chromosomeIndex = gene // n
  # 确定变异基因位于当前染色体的第几个基因位
  geneIndex = gene % n
  # mutation
  if updatepopulation[chromosomeIndex, geneIndex] == 0:
   updatepopulation[chromosomeIndex, geneIndex] = 1
  else:
   updatepopulation[chromosomeIndex, geneIndex] = 0
 return updatepopulation
 pass 

# 定义适应度函数
def fitnessFunction():
 return lambda x: 21.5 + x[0] * np.sin(4 * np.pi * x[0]) + x[1] * np.sin(20 * np.pi * x[1])
 pass 

def main(max_iter=500):
 # 每次迭代得到的最优解
 optimalSolutions = []
 optimalValues = []
 # 决策变量的取值范围
 decisionVariables = [[-3.0, 12.1], [4.1, 5.8]]
 # 得到染色体编码长度
 lengthEncode = getEncodedLength(boundarylist=decisionVariables)
 for iteration in range(max_iter):
  # 得到初始种群编码
  chromosomesEncoded = getIntialPopulation(lengthEncode, 10)
  # 种群解码
  decoded = decodedChromosome(lengthEncode, chromosomesEncoded, decisionVariables)
  # 得到个体适应度值和个体的累积概率
  evalvalues, cum_proba = getFitnessValue(fitnessFunction(), decoded)
  # 选择新的种群
  newpopulations = selectNewPopulation(chromosomesEncoded, cum_proba)
  # 进行交叉操作
  crossoverpopulation = crossover(newpopulations)
  # mutation
  mutationpopulation = mutation(crossoverpopulation)
  # 将变异后的种群解码，得到每轮迭代最终的种群
  final_decoded = decodedChromosome(lengthEncode, mutationpopulation, decisionVariables)
  # 适应度评价
  fitnessvalues, cum_individual_proba = getFitnessValue(fitnessFunction(), final_decoded)
  # 搜索每次迭代的最优解，以及最优解对应的目标函数的取值
  optimalValues.append(np.max(list(fitnessvalues)))
  index = np.where(fitnessvalues == max(list(fitnessvalues)))
  optimalSolutions.append(final_decoded[index[0][0], :])
 # 搜索最优解
 optimalValue = np.max(optimalValues)
 optimalIndex = np.where(optimalValues == optimalValue)
 optimalSolution = optimalSolutions[optimalIndex[0][0]]
 return optimalSolution, optimalValue 

solution, value = main()
print('最优解: x1, x2')
print(solution[0], solution[1])
print('最优目标函数值:', value)
# 测量运行时间
elapsedtime = timeit.timeit(stmt=main, number=1)
print('Searching Time Elapsed:(S)', elapsedtime) 

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

您可能感兴趣的文章:

• Python决策树和随机森林算法实例详解
• python实现随机森林random forest的原理及方法
• 用Python实现随机森林算法的示例
• python实现K最近邻算法
• Python实现KNN邻近算法
• python机器学习案例教程——K最近邻算法的实现
• python实现决策树C4.5算法详解(在ID3基础上改进)
• 基于ID3决策树算法的实现(Python版)
• python实现ID3决策树算法
• python实现决策树分类算法
• Python机器学习之决策树算法
• Python实现的随机森林算法与简单总结