Python数据可视化:幂律分布实例详解

1、公式推导

对幂律分布公式：

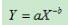
对公式两边同时取以10为底的对数：

所以对于幂律公式，对X,Y取对数后，在坐标轴上为线性方程。

2、可视化

从图形上来说，幂律分布及其拟合效果：

对X轴与Y轴取以10为底的对数。效果上就是X轴上1与10，与10与100的距离是一样的。

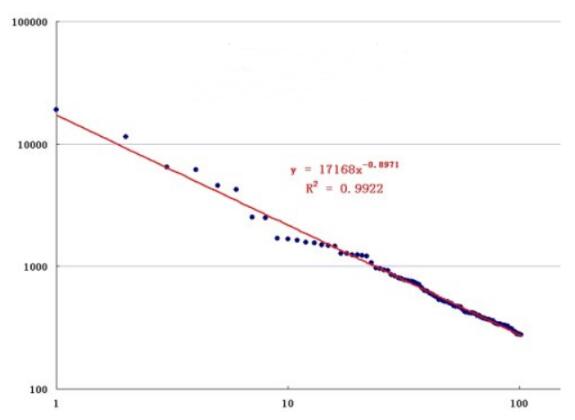
对XY取双对数后，坐标轴上点可以很好用直线拟合。所以，判定数据是否符合幂律分布，只需要对XY取双对数，判断能否用一个直线很好拟合就行。常见的直线拟合效果评估标准有拟合误差平方和、R平方。

3、代码实现

#!/usr/bin/env python
# -*-coding:utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
from scipy.stats import norm

def DataGenerate():
 X = np.arange(10, 1010, 10) # 0-1，每隔着0.02一个数据 0处取对数,会时负无穷 生成100个数据点
 noise=norm.rvs(0, size=100, scale=0.2) # 生成50个正态分布 scale=0.1控制噪声强度
 Y=[]
 for i in range(len(X)):
  Y.append(10.8*pow(X[i],-0.3)+noise[i]) # 得到Y=10.8*x^-0.3+noise

 # plot raw data
 Y=np.array(Y)
 plt.title("Raw data")
 plt.scatter(X, Y, color='black')
 plt.show()

 X=np.log10(X) # 对X，Y取双对数
 Y=np.log10(Y)
 return X,Y

def DataFitAndVisualization(X,Y):
 # 模型数据准备
 X_parameter=[]
 Y_parameter=[]
 for single_square_feet ,single_price_value in zip(X,Y):
  X_parameter.append([float(single_square_feet)])
  Y_parameter.append(float(single_price_value))

 # 模型拟合
 regr = linear_model.LinearRegression()
 regr.fit(X_parameter, Y_parameter)
 # 模型结果与得分
 print('Coefficients: \n', regr.coef_,)
 print("Intercept:\n",regr.intercept_)
 # The mean square error
 print("Residual sum of squares: %.8f"
  % np.mean((regr.predict(X_parameter) - Y_parameter) ** 2)) # 残差平方和

 # 可视化
 plt.title("Log Data")
 plt.scatter(X_parameter, Y_parameter, color='black')
 plt.plot(X_parameter, regr.predict(X_parameter), color='blue',linewidth=3)

 # plt.xticks(())
 # plt.yticks(())
 plt.show()

if __name__=="__main__":
 X,Y=DataGenerate()
 DataFitAndVisualization(X,Y)

以上这篇Python数据可视化:幂律分布实例详解就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python数据可视化:泊松分布详解

    一个服从泊松分布的随机变量X,表示在具有比率参数(rate parameter)λ的一段固定时间间隔内,事件发生的次数.参数λ告诉你该事件发生的比率.随机变量X的平均值和方差都是λ. 代码实现: # Poisson分布 x = np.random.poisson(lam=5, size=10000) # lam为λ size为k pillar = 15 a = plt.hist(x, bins=pillar, normed=True, range=[0, pillar], color='g',

  • python-numpy-指数分布实例详解

    如下所示: # Seed random number generator np.random.seed(42) # Compute mean no-hitter time: tau tau = np.mean(nohitter_times) # Draw out of an exponential distribution with parameter tau: inter_nohitter_time inter_nohitter_time = np.random.exponential(tau

  • Python数据可视化实现正态分布（高斯分布）

    正态分布(Normal distribution)又成为高斯分布(Gaussian distribution) 若随机变量X服从一个数学期望为.标准方差为的高斯分布,记为: 则其概率密度函数为: 正态分布的期望值决定了其位置,其标准差决定了分布的幅度.因其曲线呈钟形,因此人们又经常称之为钟形曲线.我们通常所说的标准正态分布是的正态分布: 概率密度函数 代码实现: # Python实现正态分布 # 绘制正态分布概率密度函数 u = 0 # 均值μ u01 = -2 sig = math.sqrt(

  • Python数据可视化:幂律分布实例详解

    1.公式推导 对幂律分布公式: 对公式两边同时取以10为底的对数: 所以对于幂律公式,对X,Y取对数后,在坐标轴上为线性方程. 2.可视化 从图形上来说,幂律分布及其拟合效果: 对X轴与Y轴取以10为底的对数.效果上就是X轴上1与10,与10与100的距离是一样的. 对XY取双对数后,坐标轴上点可以很好用直线拟合.所以,判定数据是否符合幂律分布,只需要对XY取双对数,判断能否用一个直线很好拟合就行.常见的直线拟合效果评估标准有拟合误差平方和.R平方. 3.代码实现 #!/usr/bin/env

  • Python数据可视化之Seaborn的使用详解

    Python数据可视化之Seaborn的使用详解

    目录 1. 安装 seaborn 2.准备数据 3.背景与边框 3.1 设置背景风格 3.2 其他 3.3 边框控制 4. 绘制 散点图 5. 绘制 折线图 5.1 使用 replot()方法 5.2 使用 lineplot()方法 6. 绘制直方图 displot() 7. 绘制条形图 barplot() 8. 绘制线性回归模型 9. 绘制 核密度图 kdeplot() 9.1 一般核密度图 9.2 边际核密度图 10. 绘制 箱线图 boxplot() 11. 绘制 提琴图 violinpl

  • Python数据可视化:顶级绘图库plotly详解

    有史以来最牛逼的绘图工具,没有之一 plotly是现代平台的敏捷商业智能和数据科学库,它作为一款开源的绘图库,可以应用于Python.R.MATLAB.Excel.JavaScript和jupyter等多种语言,主要使用的js进行图形绘制,实现过程中主要就是调用plotly的函数接口,底层实现完全被隐藏,便于初学者的掌握. 下面主要从Python的角度来分析plotly的绘图原理及方法: ###安装plotly: 使用pip来安装plotly库,如果机器上没有pip,需要先进行pip的安装,这里

  • Python数据可视化实现多种图例代码详解

    前言 本文的文字及图片来源于网络,仅供学习.交流使用,不具有任何商业用途,版权归原作者所有,如有问题请及时联系我们以作处理. from math import pi import matplotlib.pyplot as plt cat = ['Speed', 'Reliability', 'Comfort', 'Safety', 'Effieciency'] values = [90, 60, 65, 70, 40] N = len(cat) x_as = [n / float(N) * 2

  • python Matplotlib数据可视化（2）：详解三大容器对象与常用设置

    上一篇博客中说到,matplotlib中所有画图元素(artist)分为两类:基本型和容器型.容器型元素包括三种:figure.axes.axis.一次画图的必经流程就是先创建好figure实例,接着由figure去创建一个或者多个axes,然后通过axes实例调用各种方法来添加各种基本型元素,最后通过axes实例本身的各种方法亦或者通过axes获取axis实例实现对各种元素的细节操控. 本篇博客继续上一节的内容,展开介绍三大容器元素创建即通过三大容器可以完成的常用设置. 1 figure 1.

  • Python机器学习应用之决策树分类实例详解

    Python机器学习应用之决策树分类实例详解

    目录 一.数据集 二.实现过程 1 数据特征分析 2 利用决策树模型在二分类上进行训练和预测 3 利用决策树模型在多分类(三分类)上进行训练与预测 三.KEYS 1 构建过程 2 划分选择 3 重要参数 一.数据集 小企鹅数据集,提取码:1234 该数据集一共包含8个变量,其中7个特征变量,1个目标分类变量.共有150个样本,目标变量为 企鹅的类别 其都属于企鹅类的三个亚属,分别是(Adélie, Chinstrap and Gentoo).包含的三种种企鹅的七个特征,分别是所在岛屿,嘴巴长度,

  • python之sqlalchemy创建表的实例详解

    python之sqlalchemy创建表的实例详解 通过sqlalchemy创建表需要三要素:引擎,基类,元素 from sqlalchemy import create_engine from sqlalchemy.ext.declarative import declarative_base from sqlalchemy import Column,Integer,String 引擎:也就是实体数据库连接 engine = create_engine('mysql+pymysql://go

  • python获取指定时间差的时间实例详解

    python获取指定时间差的时间实例详解 在分析数据的时间经常需要截取一定范围时间的数据,比如三天之内,两小时前等等时间要求的数据,因此将该部分经常需要用到的功能模块化,方便以后以后用到的时候复用.在此,也分享给大家. import time import sys reload(sys) def get_day_of_day(UTC=False, days=0, hours=0, miutes=0, seconds=0): ''''''' if days>=0,date is larger th

  • Python使用struct处理二进制的实例详解

    Python使用struct处理二进制的实例详解 有的时候需要用python处理二进制数据,比如,存取文件,socket操作时.这时候,可以使用python的struct模块来完成.可以用 struct来处理c语言中的结构体. struct模块中最重要的三个函数是pack(), unpack(), calcsize() pack(fmt, v1, v2, ...)     按照给定的格式(fmt),把数据封装成字符串(实际上是类似于c结构体的字节流) unpack(fmt, string)   

  • python算法与数据结构之冒泡排序实例详解

    一.冒泡排序介绍 冒泡排序(英语:Bubble Sort)是一种简单的排序算法.它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来.遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成.这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端. 二.冒泡排序原理 比较相邻的元素.如果第一个比第二个大,就交换他们两个. 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对.这一步做完,最后的元素应该会是最大的数. 针对所有的

随机推荐