详细总结各种排序算法(Java实现)

一、插入类排序

1.直接插入排序

思想：将第i个插入到前i-1个中的适当位置

时间复杂度：T(n) = O(n²)。

空间复杂度：S(n) = O(1)。

稳定性：稳定排序。

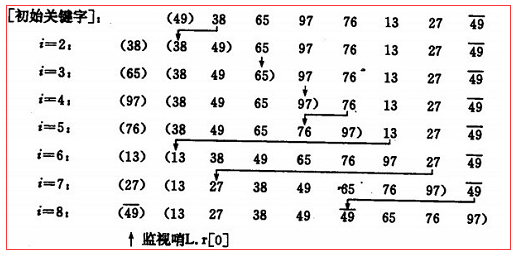
如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。

所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定

哨兵有两个作用：

① 进人查找(插入位置)循环之前，它保存了R[i]的副本，使不致于因记录后移而丢失R[i]的内容；

② 它的主要作用是：在查找循环中"监视"下标变量j是否越界。一旦越界(即j=0)，因为R[0].可以和自己比较，循环判定条件不成立使得查找循环结束，从而避免了在该循环内的每一次均要检测j是否越界(即省略了循环判定条件"j>=1")

public void insertSort(int[] array){
  for(int i=1;i<array.length;i++)//第0位独自作为有序数列，从第1位开始向后遍历
  {
   if(array[i]<array[i-1])//0~i-1位为有序，若第i位小于i-1位，继续寻位并插入，否则认为0~i位也是有序的，忽略此次循环，相当于continue
   {
    int temp=array[i];//保存第i位的值
    int k = i - 1;
    for(int j=k;j>=0 && temp<array[j];j--)//从第i-1位向前遍历并移位，直至找到小于第i位值停止
    {
     array[j+1]=array[j];
     k--;
    }
    array[k+1]=temp;//插入第i位的值
   }
  }
}

2.折半插入排序

思想：将数据插入到已经排好序的序列中，通过不断与中间点比较大小来确定位置

时间复杂度：比较时的时间减为O(n㏒n)，但是移动元素的时间耗费未变，所以总是得时间复杂度还是O(n²)。

空间复杂度：S(n) = O(1)。

稳定性：稳定排序。

3.希尔排序

思想：又称缩小增量排序法。把待排序序列分成若干较小的子序列，然后逐个使用直接插入排序法排序，最后再对一个较为有序的序列进行一次排序，主要是为了减少移动的次数，提高效率。原理应该就是从无序到渐渐有序，要比直接从无序到有序移动的次数会少一些。

时间复杂度：O(n的1.5次方)

空间复杂度：O(1)

稳定性：不稳定排序。{2,4,1,2}，2和1一组4和2一组，进行希尔排序，第一个2和最后一个2会发生位置上的变化。

public static void main(String [] args)
{
 int[]a={49,38,65,97,76,13,27,49,78,34,12,64,1};
  System.out.println("排序之前：");
  for(int i=0;i<a.length;i++)
  {
   System.out.print(a[i]+" ");
  }
  //希尔排序
  int d=a.length;
   while(true)
   {
    d=d/2;
    for(int x=0;x<d;x++)
    {
     for(int i=x+d;i<a.length;i=i+d)
     {
      int temp=a[i];
      int j;
      for(j=i-d;j>=0&&a[j]>temp;j=j-d)
      {
       a[j+d]=a[j];
      }
      a[j+d]=temp;
     }
    }
    if(d==1)
    {
     break;
    }
   }
   System.out.println();
   System.out.println("排序之后：");
    for(int i=0;i<a.length;i++)
    {
     System.out.print(a[i]+" ");
    }
  }
}

二、交换类排序

1.冒泡排序

时间复杂度：T(n) = O(n²)。

空间复杂度：S(n) = O(1)。

稳定性：稳定排序。

public class BubbleSort
{
 public void sort(int[] a)
 {
  int temp = 0;
  for (int i = a.length - 1; i > 0; --i)
  {
   for (int j = 0; j < i; ++j)
   {
    if (a[j + 1] < a[j])
    {
     temp = a[j];
     a[j] = a[j + 1];
     a[j + 1] = temp;
    }
   }
  }
 }
}

2.快速排序

思想：对冒泡排序的改进，通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

时间复杂度：平均T(n) = O(n㏒n)，最坏O(n²)。

空间复杂度：S(n) = O(㏒n)。

稳定性：不稳定排序

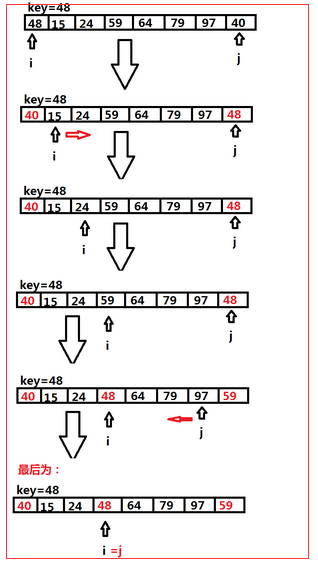
首先把数组的第一个数拿出来做为一个key，在前后分别设置一个i,j做为标识，然后拿这个key对这个数组从后面往前遍历，及j--，直到找到第一个小于这个key的那个数，然后交换这两个值，交换完成后，我们拿着这个key要从i往后遍历了，及i++;一直循环到i=j结束，当这里结束后，我们会发现大于这个key的值都会跑到这个key的后面

三、选择类排序

1.简单选择排序

时间复杂度：T(n) = O(n²)。

空间复杂度：S(n) = O(1)。

稳定性：不稳定排序

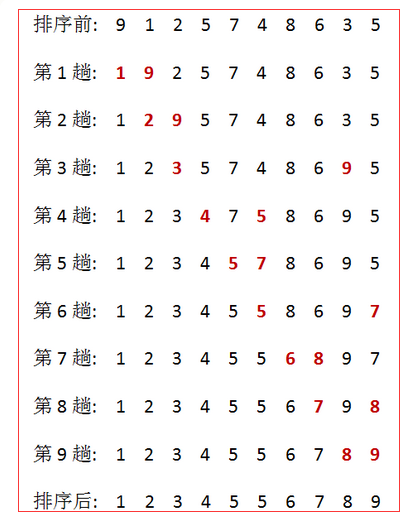
思路：

1）从待排序的序列中，找到关键字最小的元素

2）如果最小的元素不在第一位，就和第一个元素互换位置

3）从余下的N-1个元素中，找到关键字最小的元素，重复 1）、2）步

public class SelectionSort {
 public void selectionSort(int[] list) {
  // 需要遍历获得最小值的次数
  // 要注意一点，当要排序 N 个数，已经经过 N-1 次遍历后，已经是有序数列
  for (int i = 0; i < list.length - 1; i++) {
   int temp = 0;
   int index = i; // 用来保存最小值得索引
   // 寻找第i个小的数值
   for (int j = i + 1; j < list.length; j++) {
    if (list[index] > list[j]) {
     index = j;
    }
   }
   // 将找到的第i个小的数值放在第i个位置上
   temp = list[index];
   list[index] = list[i];
   list[i] = temp;
   System.out.format("第 %d 趟:\t", i + 1);
   printAll(list);
  }
 }
 // 打印完整序列
 public void printAll(int[] list) {
  for (int value : list) {
   System.out.print(value + "\t");
  }
  System.out.println();
 }
 public static void main(String[] args) {
  // 初始化一个随机序列
  final int MAX_SIZE = 10;
  int[] array = new int[MAX_SIZE];
  Random random = new Random();
  for (int i = 0; i < MAX_SIZE; i++) {
   array[i] = random.nextInt(MAX_SIZE);
  }
  // 调用排序方法
  SelectionSort selection = new SelectionSort();
  System.out.print("排序前:\t");
  selection.printAll(array);
  selection.selectionSort(array);
  System.out.print("排序后:\t");
  selection.printAll(array);
 }
}

2.树形选择排序

思想：为了减少比较次数，两两进行比较，得出的较小的值再两两比较，直至得出最小的输出，然后在原来位置上置为∞，再进行比较。直至所有都输出。

时间复杂度：T(n) = O(n㏒n)。

空间复杂度：较简单选择排序，增加了n-1个额外的存储空间存放中间比较结果，就是树形结构的所有根节点。S(n) = O(n)。

稳定性：稳定排序。

3.堆排序

【待】

四.、归并排序

归并排序：

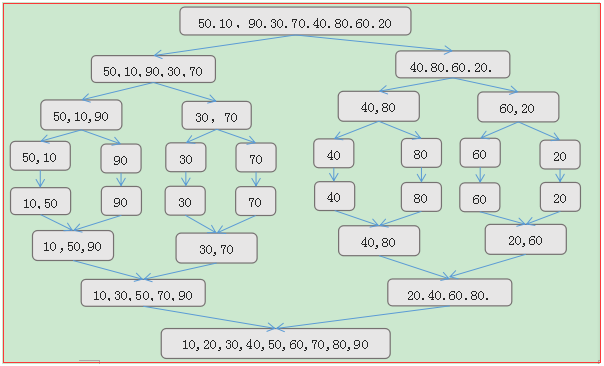
思想：假设初始序列有n个记录，首先将这n个记录看成n个有序的子序列，每个子序列的长度为1，然后两两归并，得到n/2向上取整个长度为2（n为奇数时，最后一个序列的长度为1）的有序子序列

在此基础上，在对长度为2的有序子序列进行两两归并，得到若干个长度为4的有序子序列　　

如此重复，直至得到一个长度为n的有序序列为止。

时间复杂度：T(n) = O(n㏒n)

空间复杂度：S(n) = O(n)

稳定性：稳定排序

public class MergeSort {

 public static void merge(int[] a, int low, int mid, int high) {
  int[] temp = new int[high - low + 1];
  int i = low;// 左指针
  int j = mid + 1;// 右指针
  int k = 0;
  // 把较小的数先移到新数组中
  while (i <= mid && j <= high) {
   if (a[i] < a[j]) {
    temp[k++] = a[i++];
   } else {
    temp[k++] = a[j++];
   }
  }
  // 把左边剩余的数移入数组
  while (i <= mid) {
   temp[k++] = a[i++];
  }
  // 把右边边剩余的数移入数组
  while (j <= high) {
   temp[k++] = a[j++];
  }
  // 把新数组中的数覆盖nums数组
  for (int k2 = 0; k2 < temp.length; k2++) {
   a[k2 + low] = temp[k2];
  }
 }

 public static void mergeSort(int[] a, int low, int high) {
  int mid = (low + high) / 2;
  if (low < high) {
   // 左边
   mergeSort(a, low, mid);
   // 右边
   mergeSort(a, mid + 1, high);
   // 左右归并
   merge(a, low, mid, high);
   System.out.println(Arrays.toString(a));
  }

 }

 public static void main(String[] args) {
  int a[] = { 51, 46, 20, 18, 65, 97, 82, 30, 77, 50 };
  mergeSort(a, 0, a.length - 1);
  System.out.println("排序结果：" + Arrays.toString(a));
 }
}

五、分配类排序

1.多关键字排序：

【待】

2.链式基数排序：

思想：先分配，再收集，就是先按照一个次关键字收集一下，然后进行收集（第一个排序），然后再换一个关键字把新序列分配一下，然后再收集起来，又完成一次排序，这样所有关键字分配收集完后，就完成了排序。

时间复杂度：T(n) = O( d ( n + rd ) )

空间复杂度：S(n) = O(rd)

稳定性：稳定排序

以上这篇详细总结各种排序算法(Java实现)就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。