C语言用递归函数实现汉诺塔

目录
  • 汉诺塔（Hanoi）是什么？
  • 那么，C语言如何实现汉诺塔呢？
  • 汉诺塔的基本思路是：
  • 具体代码见下（注意点在代码下面）：
  • 总结

汉诺塔（Hanoi）是什么？

一个简单的汉诺塔就如上图所示，有三个放置点，放置物必须遵循上小下大的规则，依次将1中的放置物全部放置到3中。就比如该图中有4个放置物，若将A上的放置物全部移至C上，具体的步骤是：A->B A->C B->C A->B C->A C->B A->B A->C B->C B->A C->A B->C A->B A->C B->C。

那么，C语言如何实现汉诺塔呢？

第一步要先确定起始位置、中转位置、目的位置，在一开始A是起始位置，B是中转位置，C是目的位置，在后续移动物块的时候会一直改变这三个位置的功能，以达到最终目标。

汉诺塔的基本思路是：

第一阶段：将n-1个物块（也就是除最底部的物块外）经过一系列地堆放（这里就可以使用到递归的方法来实现），最后放置到中转位置上，然后把起始位置剩下的物块放到目的位置上，如下图：

以上一系列地堆放是指：以A为起始位置，C为中转位置，B为目的位置，也就相当于把C看作是一个中间存放点，来帮助这n-1个物块放到B里面去。

第二阶段：然后会发现，变化后的汉诺塔的形式也和之前是差不多的，如果把B看作是起始位置，A是中转位置，C是目的位置。就可以一直按照上面的那个方法一直递归下去，如下图：

以此类推……最后就能实现把所有的物块全部从A搬到C。

具体代码见下（注意点在代码下面）：

//C语言实现汉诺塔
#include <stdio.h>

void move(char p1, char p2)
{
	printf("%c->%c  ", p1, p2);
}

//n:个数  pos1:起始位置  pos2:中转位置  pos3:目的位置
void Hanoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1)
	{
		move(pos1, pos3);
	}
	else
	{
		Hanoi(n - 1, pos1, pos3, pos2);
		move(pos1, pos3);
		Hanoi(n - 1, pos2, pos1, pos3);
	}
}

int main()
{
	Hanoi(1, 'A', 'B', 'C');
	printf("\n");
	Hanoi(2, 'A', 'B', 'C');
	printf("\n");
	Hanoi(3, 'A', 'B', 'C');
	printf("\n");
	Hanoi(4, 'A', 'B', 'C');
	printf("\n");
	return 0;
}

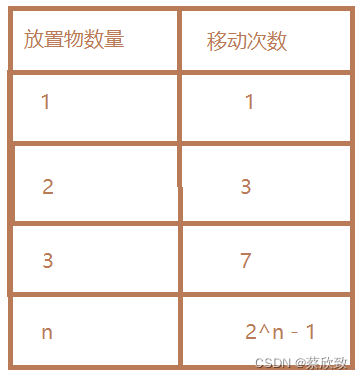
注意点一：代码中的n值不能太大，因为移动次数是随n的增大呈指数倍增长。

注意点二：n为1的时候已近到达最小单位（也就是最底层），不需要使用递归；n为大于1的值时，需要递归到1才能进行。

注意点三：第一阶段使用递归表示的是把上面n-1层全部移到B中；而第二阶段使用递归表示的是把B中全部移到C中。

总结

这样就可以简单地完成汉诺塔，此代码并不是最优方法，但是理解起来比较容易。递归在实际中运用的不是很多，但是也要看得懂代码和写出类似这种汉诺塔等递归函数的基础代码。

到此这篇关于C语言用递归函数实现汉诺塔的文章就介绍到这了,更多相关C语言汉诺塔内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • C语言编程递归算法实现汉诺塔

    C语言编程递归算法实现汉诺塔

    汉诺塔 法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针.印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔.不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面.僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔.庙宇和众生也都将同归于尽. 这个传说挺有意思的,这个传说

  • C语言递归思想实现汉诺塔详解

    C语言递归思想实现汉诺塔详解

    目录 1.递归思想简介 2.汉诺塔问题 3.汉诺塔递归的c语言实现 总结 1.递归思想简介 在c语言中,程序调用自身的编程技巧称为递归( recursion). 递归的定义看上去似乎很抽象,使用代码描述能够让人容易理解,下面是一个函数递归的例子. /* 递归求n的阶乘 */ int factorial(int n) //定义一个求阶乘的函数叫做factorial(),需要一个整形参数,返回一个整形值 { if (n <= 1) //递归结束的条件 { return 1; } else { ret

  • C语言递归之汉诺塔和青蛙跳台阶问题

    C语言递归之汉诺塔和青蛙跳台阶问题

    递归就是一个函数执行过程中调用自己,在c语言中有很多关于递归的经典问题,例如:斐波那契数列问题.汉诺塔问题等,在研究递归问题时我们要注意三点: 1.递归的结束条件 2.递归在每次进行过程中,都得离条件越来越近 3.相邻两次递归调用之间的关联关系 汉诺塔问题: 有三根杆子A, B, C.A杆上有N个(N > 1)穿孔圆盘, 盘的尺寸由下到上依次变小.要求按下列规则将所有圆盘移至C杆: 1.每次只能移动一个圆盘: 2.大盘不能叠在小盘上面,可将圆盘临时置于B杆, 也可将从A杆移出的圆盘重新移回A杆,

  • C语言用递归函数实现汉诺塔

    C语言用递归函数实现汉诺塔

    目录 汉诺塔(Hanoi)是什么? 那么,C语言如何实现汉诺塔呢? 汉诺塔的基本思路是: 具体代码见下(注意点在代码下面): 总结 汉诺塔(Hanoi)是什么? 一个简单的汉诺塔就如上图所示,有三个放置点,放置物必须遵循上小下大的规则,依次将1中的放置物全部放置到3中.就比如该图中有4个放置物,若将A上的放置物全部移至C上,具体的步骤是:A->B A->C B->C A->B C->A C->B A->B A->C B->C B->A C->

  • C语言递归函数与汉诺塔问题简明理解

    目录 递归函数 Hanio(汉诺塔)问题 递归函数 直接或者间接调用函数本身.“自己调用自己” 什么情况下面可以使用递归呢? 解决一个问题时,解决思路化成与问题本身类似的问题时,“递归” 是不是所有的递归问题,C语言都能支持呢? 不是的 C语言能够解决的递归问题,必须要满足两个条件: (1) 问题本身一个递归问题. (2) 递归不能是无限递归 适合那些递归到一定程度时,答案是显而易见的. 一定需要有一个“跳出无限递归的条件”. C语言是如何支持递归呢? int age(int n) //从425

  • JavaScript递归函数解“汉诺塔”算法代码解析

    "汉诺塔"是一个著名的益智游戏.塔上有3根柱子和一套直径各不相同的空心圆盘.开始时柱子上的所有圆盘都按照从小到大的顺序堆叠.目标是通过每次移动一个圆盘到另一根柱子,最终把一堆圆盘移动到目标柱子上,过程中不允许把交大的圆盘放置在较小的圆盘之上. 仔细解读这段话,如果有10个圆盘甚至更多,那操作步骤绝对多到让人震惊,但目标是把一堆圆盘移动到目标柱子上,如果把上面的9个圆盘看成一套,第10个圆盘看成另一套,先移动9个圆盘到另一根柱子上,再把上面8个圆盘看成一套,第9个圆盘看成另一套--依次类

  • c语言循环加数组实现汉诺塔问题

    目录 简介 递归的汉诺塔解法(c语言) 循环实现汉诺塔问题(c语言) 简介 汉诺塔问题是学数据结构与算法的时候会遇到的问题,相信来看本文的读者应该都对汉诺塔问题有基本的了解,理论上所有的递归都可以改成循环,常规的做法是借助堆栈,但是我一想好像用循环加数组也可以实现,于是就有了本文,实现声明,本文最后出来的算法效率不高的,比直接用递归实现还要差很多,追求算法效率的同学就不用看这个了.题目:假设有3个柱子,分别为A.B.C,A柱子上有数量为n个的空心圆盘,从上到下序号分别为1...n,要求把A柱子中

  • C语言实现汉诺塔游戏

    C语言实现汉诺塔游戏

    操作就是:A B 号码A的塔顶一层放在号码B的塔顶.如1(空格) 3 回车. 话说有人能把我这C的代码添加到QT界面框架上去么?  代码写的不好 ,维护性不够,只能玩8层的,写完以后发现很难拓展,软件工程,设计模式有待提高.... 里面提示输入等级的装B用了,没有实现,大家随便输入个个位数就可以玩了. stackfunc.c #include"STACK.h" #include<stdio.h> extern ceng CENG[SIZE]; //数据入栈 void pus

  • C语言汉诺塔的简单了解

    C语言汉诺塔的简单了解

    汉诺塔详解 以4层为例 以下为我的拙见,还希望大佬雅正 要把汉诺塔移动到c 需要把1,2,3层移到b 把4移动到c 在吧123移动到b 但是一次只能动一块 所以我们目前要做的就是把上面三块移动到b 那就需要把1 2移动到c 由此我们可以推出要把1,2移动到c,只需要把1移动到b 这里我们发现有很多重复的自相似动作 我们就可以设计递归 递归需要1,递归体 2 出口. 递归体 移动n-1个盘子和1个盘子和n个盘子过程都是相似的 但是每次放入的杆子不一样. 出口 n=1时只剩一个盘子,直接移动到c即可

  • C 语言基础实现青蛙跳台阶和汉诺塔问题

    C 语言基础实现青蛙跳台阶和汉诺塔问题

    目录 一.青蛙跳台阶 题目 思路 分析 1. 从跳法次数分析 2. 从过程分析 二.青蛙跳台阶变式1 题目 分析 三.青蛙跳台阶变式2 题目 分析 四.汉诺塔问题(求步数) 题目 思路 分析 五.汉诺塔问题(求移动过程) 题目 思路 分析 一.青蛙跳台阶 题目 一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶.求该青蛙跳上一个 n 级的台阶总共有多少种跳法 思路 遇见题目我们可以在纸上先动手画画,把最简单的几种方式列出来,作比较,找规律. 分析 按照上面表格可以从跳法次数,过程,或者两者结合找规

随机推荐