python实现高斯判别分析算法的例子

高斯判别分析算法（Gaussian discriminat analysis）

高斯判别算法是一个典型的生成学习算法（关于生成学习算法可以参考我的另外一篇博客）。在这个算法中，我们假设p(x|y)p(x|y)服从多元正态分布。

注：在判别学习算法中，我们假设p(y|x)p(y|x)服从一维正态分布，这个很好类比，因为在模型中输入数据XX通常是拥有很多维度的，所以对于XX的条件概率建模时要取多维正态分布。

多元正态分布

多元正态分布也叫多元高斯分布，这个分布的两个参数分别是平均向量μ∈Rnμ∈Rn和一个协方差矩阵∑∈Rn×n∑∈Rn×n

关于协方差矩阵的定义；假设XX是由nn个标量随机变量组成的列向量，并且μkμk是第kk个元素的期望值，即μk=E(Xk)μk=E(Xk)，那么协方差矩阵被定义为

下面是一些二维高斯分布的概率密度图像：

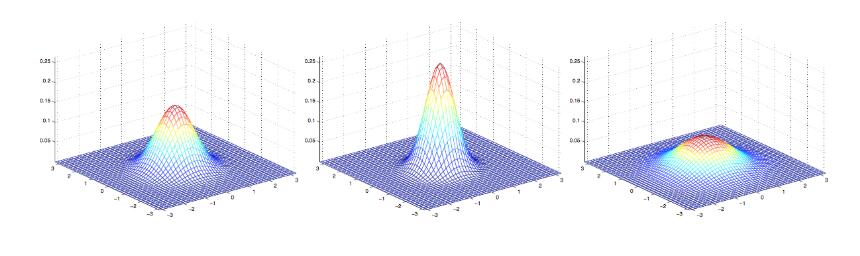
最右边的图像展现的二维高斯分布的均值是零向量（2x1的零向量），协方差矩阵Σ=IΣ=I(2x2的单位矩阵)，像这样以零向量为均值以单位阵为协方差的多维高斯分布称为标准正态分布，中间的图像以零向量为均值，Σ=0.6IΣ=0.6I;最右边的图像中Σ=2IΣ=2I，观察发现当ΣΣ越大时，高斯分布越“铺开”，当ΣΣ越小时，高斯分布越“收缩”。

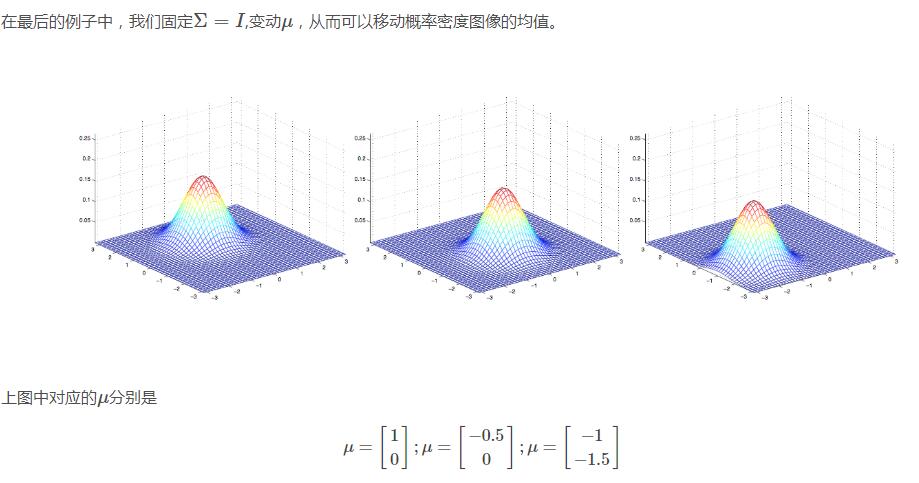
让我们看一些其他例子对比发现规律

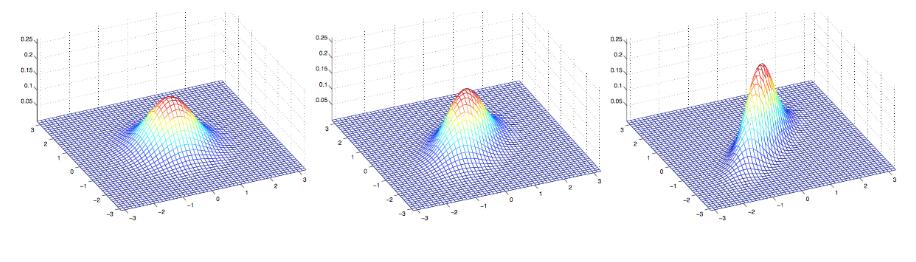
上图中展示的三个高斯分布对应的均值均为零向量，协方差矩阵分别对应与下面三个

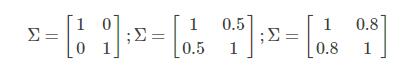
最左边的图像是我们熟悉的标准二维正态分布，然后我们观察到当我们增加ΣΣ的非主对角元素时，概率密度图像沿着45°线(x1=x2x1=x2)“收缩”，从对应的等高线轮廓图可以跟清楚的看到这一点：

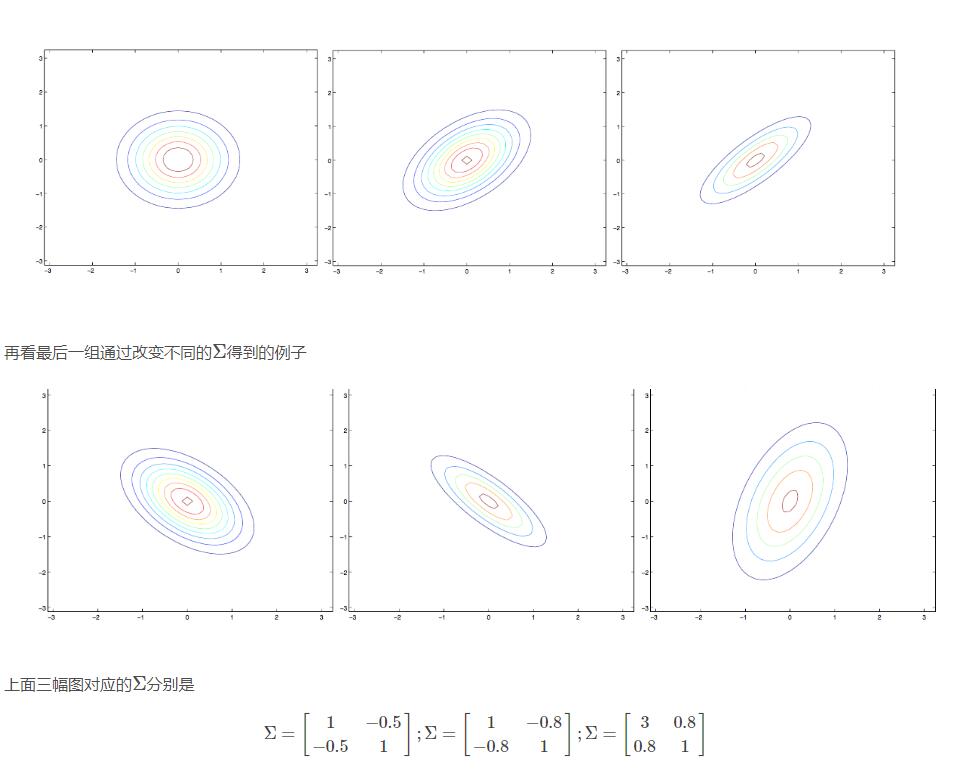
通过对比右边和中间的两幅图发现，通过减少主对角元素可以让概率密度图像变得“收缩”，不过是在相反的方向上。

高斯判别分析模型

当我们处理输入特征是连续随机变量xx时的分类问题时，我们可以使用高斯判别分析模型（GDA），用多元正态分布模型来描述p(x|y)p(x|y),模型的具体数学表达式是这样的：

通过最大化似然函数ll可以得到上面四个参数的估计值：

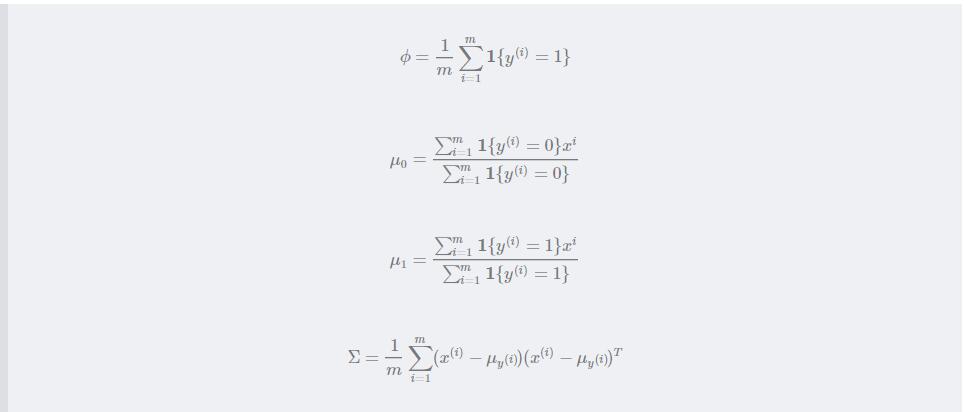
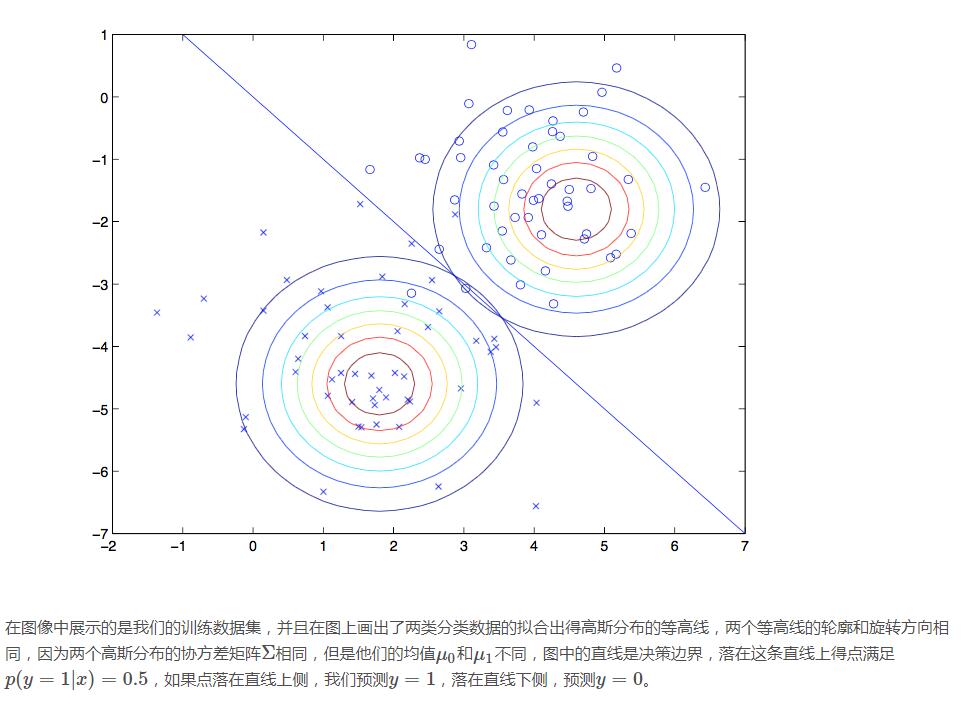
我们用图像直观的描述一下算法处理的结果：

python的实现demo 如下：

第57的高斯概率密度函数用矩阵运算写有bug没跑通，又因为实验数据只有二维，于是在纸上对上文中矩阵运算公式进行了化简至最后结果写在了函数里。如有疑问可以拿出笔来演算一下。

#GDA
#author:Xiaolewen
import matplotlib.pyplot as plt
from numpy import *

#Randomly generate two cluster data of Gaussian distributions
mean0=[2,3]
cov=mat([[1,0],[0,2]])
x0=random.multivariate_normal(mean0,cov,500).T #The first class point which labael equal 0
y0=zeros(shape(x0)[1])
#print x0,y0
mean1=[7,8]
cov=mat([[1,0],[0,2]])
x1=random.multivariate_normal(mean1,cov,300).T
y1=ones(shape(x1)[1]) #The second class point which label equals 1
#print x1,y1

x=array([concatenate((x0[0],x1[0])),concatenate((x0[1],x1[1]))])
y=array([concatenate((y0,y1))])
m=shape(x)[1]
#print x,y,m
#Caculate the parameters:\phi,\u0,\u1,\Sigma
phi=(1.0/m)*len(y1)
#print phi
u0=mean(x0,axis=1)
#print u0
u1=mean(x1,axis=1)
#print u1

xplot0=x0;xplot1=x1 #save the original data to plot
x0=x0.T;x1=x1.T;x=x.T
#print x0,x1,x
x0_sub_u0=x0-u0
x1_sub_u1=x1-u1
#print x0_sub_u0
#print x1_sub_u1
x_sub_u=concatenate([x0_sub_u0,x1_sub_u1])
#print x_sub_u

x_sub_u=mat(x_sub_u)
#print x_sub_u

sigma=(1.0/m)*(x_sub_u.T*x_sub_u)
#print sigma

#plot the discriminate boundary ,use the u0_u1's midnormal
midPoint=[(u0[0]+u1[0])/2.0,(u0[1]+u1[1])/2.0]
#print midPoint
k=(u1[1]-u0[1])/(u1[0]-u0[0])
#print k
x=range(-2,11)
y=[(-1.0/k)*(i-midPoint[0])+midPoint[1] for i in x]

#plot contour for two gaussian distributions
def gaussian_2d(x, y, x0, y0, sigmaMatrix):
 return exp(-0.5*((x-x0)**2+0.5*(y-y0)**2))
delta = 0.025
xgrid0=arange(-2, 6, delta)
ygrid0=arange(-2, 6, delta)
xgrid1=arange(3,11,delta)
ygrid1=arange(3,11,delta)
X0,Y0=meshgrid(xgrid0, ygrid0) #generate the grid
X1,Y1=meshgrid(xgrid1,ygrid1)
Z0=gaussian_2d(X0,Y0,2,3,cov)
Z1=gaussian_2d(X1,Y1,7,8,cov)

#plot the figure and add comments
plt.figure(1)
plt.clf()
plt.plot(xplot0[0],xplot0[1],'ko')
plt.plot(xplot1[0],xplot1[1],'gs')
plt.plot(u0[0],u0[1],'rx',markersize=20)
plt.plot(u1[0],u1[1],'y*',markersize=20)
plt.plot(x,y)
CS0=plt.contour(X0, Y0, Z0)
plt.clabel(CS0, inline=1, fontsize=10)
CS1=plt.contour(X1,Y1,Z1)
plt.clabel(CS1, inline=1, fontsize=10)
plt.title("Gaussian discriminat analysis")
plt.xlabel('Feature Dimension (0)')
plt.ylabel('Feature Dimension (1)')
plt.show(1)

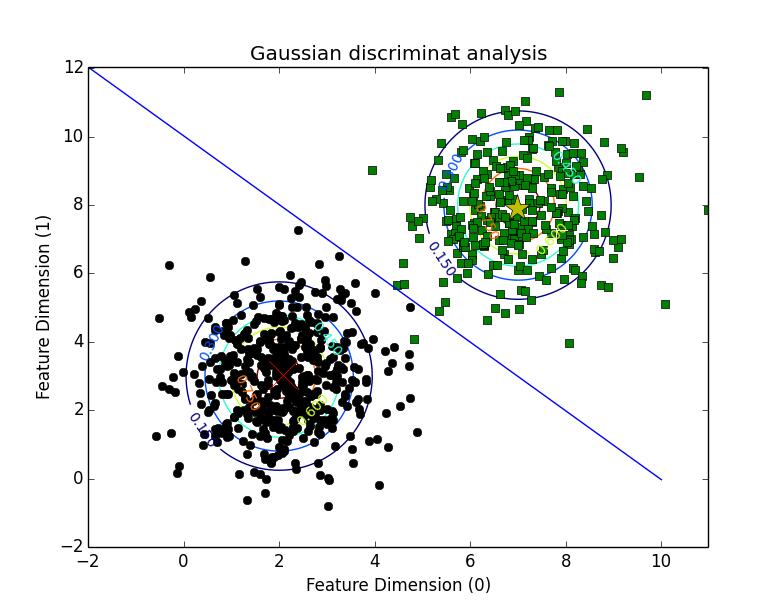
这是最终的拟合结果：

以上这篇python实现高斯判别分析算法的例子就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。