Java的递归算法详解

目录

• 一、介绍
• 1、介绍
• 2、案例
• 二、迷宫问题
• 三、八皇后问题
• 四、汉诺塔问题
• 1、问题
• 2、思想
• 3、代码
• 总结

一、介绍

1、介绍

递归：递归就是方法自己调用自己，每次调用时传入不同的变量。递归有助于编程者解决复杂的问题，同时可以让代码变得简洁。

迭代和递归区别：迭代使用的是循环结构，递归使用的选择结构。使用递归能使程序的结构更清晰、更简洁、更容易让人理解，从而减少读懂代码的时间。其时间复杂度就是递归的次数。

但大量的递归调用会建立函数的副本，会消耗大量的时间和内存，而迭代则不需要此种付出。

递归函数分为调用和回退阶段，递归的回退顺序是它调用顺序的逆序。

分治：当一个问题规模较大且不易求解的时候，就可以考虑将问题分成几个小的模块，逐一解决。

2、案例

• 兔子繁殖的问题。（斐波那契数列）。
• 计算 n! 。
• 任意长度的字符串反向输出。
• 折半查找算法的递归实现。
• 汉诺塔问题
• 八皇后问题

二、迷宫问题

问题：寻找一条从起始点到达终点的有效路径。

代码示例：迷宫

public class MiGong {
    /**
     * 0:该点没有走过, 1:表示墙, 2:可以走, 3:该点已经走过,但是走不通\
     * 策略: 下->右->上->左, 如果该点走不通，再回溯
     */
    private int[][] map;
    private int desX;
    private int desY;
    /**
     * 构建 row*col的迷宫
     *
     * @param row 行
     * @param col 列
     */
    public MiGong(int row, int col) {
        if (row <= 0 || col <= 0) {
            return;
        }
        map = new int[row][col];
        // 默认 上下左右 全部为墙
        for (int i = 0; i < col; i++) {
            map[0][i] = 1;
            map[row - 1][i] = 1;
        }
        for (int i = 0; i < row; i++) {
            map[i][0] = 1;
            map[i][col - 1] = 1;
        }
    }
    /**
     * 在迷宫内部添加挡板
     *
     * @param i 横坐标
     * @param j 纵坐标
     */
    public void addBaffle(int i, int j) {
        if (map == null) {
            return;
        }
        // 外面一周都是墙
        if (i > 0 && i < map.length - 1 && j > 0 && j < map[0].length - 1) {
            map[i][j] = 1;
        }
    }
    /**
     * 设置迷宫的终点位置
     *
     * @param desX 横坐标
     * @param desY 纵坐标
     */
    public void setDes(int desX, int desY) {
        this.desX = desX;
        this.desY = desY;
    }
    public boolean setWay(int i, int j) {
        // 通路已经找到
        if (map[desX][desY] == 2) {
            return true;
        } else {
            if (map[i][j] != 0) {
                return false;
            }
            // map[i][j] == 0 按照策略 下->右->上->左 递归
            // 假定该点是可以走通.
            map[i][j] = 2;
            if (setWay(i + 1, j)) {
                return true;
            } else if (setWay(i, j + 1)) {
                return true;
            } else if (setWay(i - 1, j)) {
                return true;
            } else if (setWay(i, j - 1)) {
                return true;
            } else {
                // 说明该点是走不通，是死路
                map[i][j] = 3;
                return false;
            }
        }
    }
    // 显示地图
    public void show() {
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[0].length; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
    }
}

　　代码示例：测试类

// 测试类
public class Main {
    public static void main(String[] args) {
        MiGong miGong = new MiGong(8, 7);
        miGong.addBaffle(3, 1);
        miGong.addBaffle(3, 2);
        miGong.setDes(6, 5); // 设置目的地
        System.out.println("初始地图的情况");
        miGong.show();
        miGong.setWay(1, 1); // 设置起始位置
        System.out.println("小球走过的路径,地图的情况");
        miGong.show();
    }
}

// 结果
初始地图的情况
1 1 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1
小球走过的路径,地图的情况
1 1 1 1 1 1 1
1 2 0 0 0 0 1
1 2 2 2 0 0 1
1 1 1 2 0 0 1
1 0 0 2 0 0 1
1 0 0 2 0 0 1
1 0 0 2 2 2 1
1 1 1 1 1 1 1

三、八皇后问题

问题：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即：任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

代码示例：八皇后

public class Queue8 {
    private static final int MAX = 8;
    // 保存皇后放置的位置,比如 arr = {0, 4, 7, 5, 2, 6, 1, 3}
    private final int[] array = new int[MAX];
    public static int count = 0;
    public static int judgeCount = 0;
    public void check() {
        this.check(0);
    }
    // check 是每一次递归时，进入到check中都有 for(int i = 0; i < max; i++)，因此会有回溯
    private void check(int n) {
        // n = 8, 表示8个皇后就已经放好
        if (n == MAX) {
            print();
            return;
        }
        for (int i = 0; i < MAX; i++) {
            array[n] = i;

            // 判断当放置第n个皇后到i列时，是否冲突
            // 不冲突
            if (!judge(n)) {
                // 接着放n+1个皇后,即开始递归
                check(n + 1);
            }
        }
    }
    private boolean judge(int n) {
        judgeCount++;
        for (int i = 0; i < n; i++) {
            // 同一列 或 同一斜线
            if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
                return true;
            }
        }
        return false;
    }
    private void print() {
        count++;
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }

}

代码示例：测试类

// 测试类
public class Main {
    public static void main(String[] args) {
        Queue8 queue8 = new Queue8();
        queue8.check();
        System.out.printf("一共有%d解法", Queue8.count);
        System.out.printf("一共判断冲突的次数%d次", Queue8.judgeCount); // 1.5w
    }
}

四、汉诺塔问题

1、问题

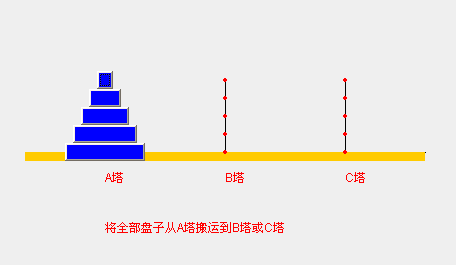
2、思想

如果 n = 1，A -> C

如果 n >= 2，总是看做是两个盘，①最下边的盘。②上面所有的盘。则，步骤：

（1）先把上面所有的盘 A->B

（2）把最下边的盘 A->C

（3）把 B 塔的所有盘 从 B->C

3、代码

代码示例：汉诺塔问题

// 汉诺塔
public class Hanoitower {
    // 使用分治算法
    public static void move(int num, char a, char b, char c) {
        // 如果只有一个盘
        if (num == 1) {
            System.out.println("第1个盘从 " + a + "->" + c);
        } else {
            // n >= 2，总是看做是两个盘，①最下边的盘。②上面所有的盘。则，步骤：
            // 1.先把上面所有的盘 A->B.移动过程会使用到 c
            move(num - 1, a, c, b);
            // 2.把最下边的盘 A->C
            System.out.println("第" + num + "个盘从 " + a + "->" + c);
            // 3.把 B 塔的所有盘 从 B->C.移动过程会使用到 a
            move(num - 1, b, a, c);
        }
    }
}

代码示例：测试类

// 测试类
public class Main {
    public static void main(String[] args) {
        Hanoitower.move(3, 'A', 'B', 'C');
    }
}

// 结果
第1个盘从 A->C
第2个盘从 A->B
第1个盘从 C->B
第3个盘从 A->C
第1个盘从 B->A
第2个盘从 B->C
第1个盘从 A->C

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注我们的更多内容！