python机器学习MATLAB最小二乘法的两种解读

目录
  • 最小二乘法
    • 代价函数与最小二乘法
    • 向量到子空间的距离与最小二乘法
    • 最小二乘法与多项式拟合
    • 多项式拟合结果绘图：
    • 最小二乘法与多元线性回归
    • 多元线性回归结果绘图：

最小二乘法

大部分的最小二乘法公式推导，都是使用的 代价函数偏导 的方式来求得的，在这里首先展示如何通过代价函数求偏导的方式得到最小二乘公式，再展示李扬老师讲解的如何由向量到子空间的距离得来最小二乘法公式。

代价函数与最小二乘法

假设我们的拟合结果为：

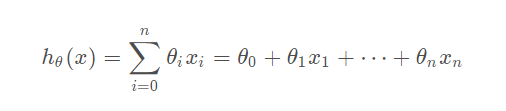
则平方损失函数为：

平方损失函数的形式只有极小值，没有极大值，我们要使代价函数最小，我们要找到其极值点，即偏导均为0的点，代价函数对于各参数偏导如下：

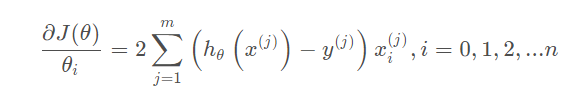
令偏导为0得：

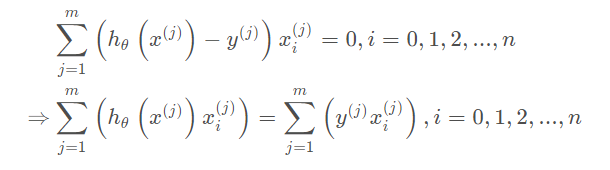
实际上若是令:

则有：

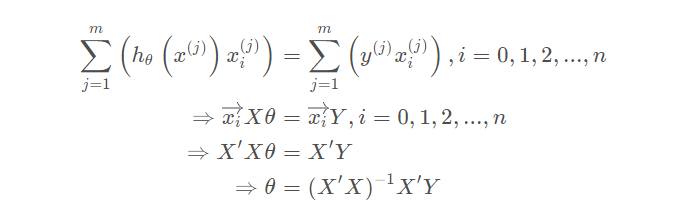
向量到子空间的距离与最小二乘法

最小二乘法与多项式拟合

以下展示自己编写最小二乘法拟合多项式与MATLAB自带函数 polyfit 拟合多项式的参数对比，注意，为了和MATLAB自带函数保持一致，θ向量变为第一个参数为 θn  ,最后一个参数为 θo  , X 矩阵也做了相应的调整：

% 最小二乘法多项式拟合
% 原三次函数+随机噪声
f=@(x)x.^3+6.*x.^2-2.*x+4+(rand(size(x))-.5).*20;
% 构造原始数据
x=-5:.1:5;
y=f(x);
% 自己写一个最小二乘
n=3;% 最高次数为三次
X=(x').^(n:-1:0);
theta1=((X'*X)\X'*y')';
% MATLAB自带多项式拟合
theta2=polyfit(x,y,n);
% 输出对比
disp(theta1)
disp(theta2)
% 一个小技巧，下面的写法能够快速将
% 参数向量变成有关x的多项式匿名函数
func=matlabFunction(poly2sym(theta1));

theta1=
0.9686 6.0178 -1.8845 4.3362
theta2=
0.9686 6.0178 -1.8845 4.3362

多项式拟合结果绘图：

% 绘图部分
% 保持坐标区域不刷新并添加网格
ax=gca;hold(ax,'on');grid(ax,'on');
% 绘制原数据点和拟合结果
plot(x,y,'o','MarkerFaceColor',[94,142,179]./255);
plot(x,func(x),'Color',[0,64,115]./255,'LineWidth',2);
% 修饰一下
ax.FontName='cambria';
ax.LineWidth=1.5;
ax.GridLineStyle='--';
ax.XColor=[1,1,1].*.3;
ax.YColor=[1,1,1].*.3;
ax.ZColor=[1,1,1].*.3;

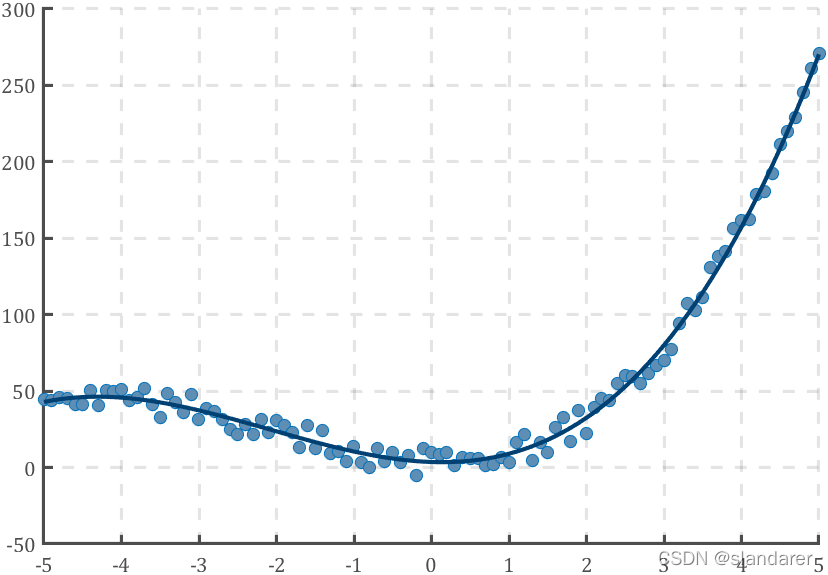
最小二乘法与多元线性回归

以下展示自己编写最小二乘法进行多元线性回归与MATLAB自带函数 regress 进行多元线性回归的参数对比：

% 最小二乘法多元线性回归
% 原二元函数+随机噪声
f=@(x1,x2) 3.*x1+4.*x2+5+(rand(size(x1))-.5).*10;
% 构造原始数据
[x1,x2]=meshgrid(-5:.5:5,-5:.5:5);
y=f(x1,x2);
% 自己写一个最小二乘
X=[x1(:),x2(:),ones(size(x1(:)))];
theta1=((X'*X)\X'*y(:));
% MATLAB多元线性回归
theta2=regress(y(:),X);
% 输出对比
disp(theta1)
disp(theta2)
% 构造拟合结果的二元匿名函数
func=matlabFunction([sym('x1'),sym('x2'),1]*theta1);

theta1=
2.9285 4.0688 4.7520
theta2=
2.9285 4.0688 4.7520

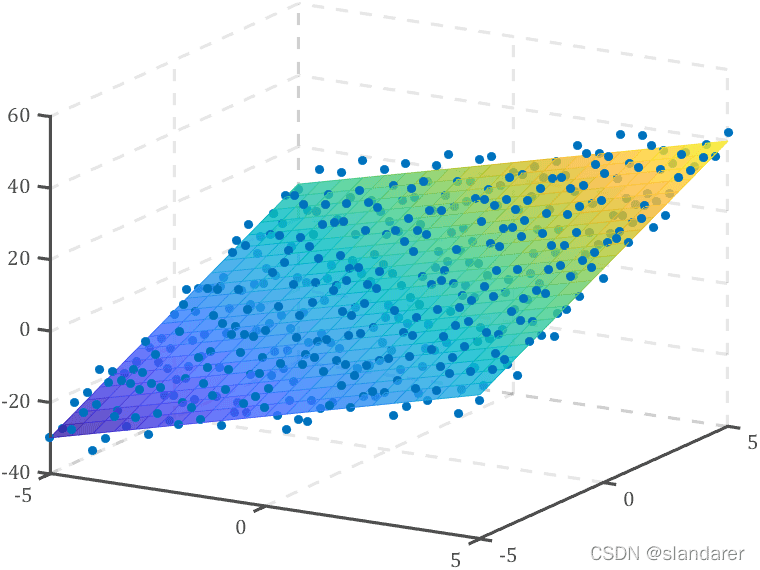
多元线性回归结果绘图：

% 绘图部分
% 保持坐标区域不刷新并添加网格
ax=gca;hold(ax,'on');grid(ax,'on');
% 绘制原数据点和拟合结果
mesh(x1,x2,func(x1,x2),'FaceColor','flat','FaceAlpha',.8)
scatter3(x1(:),x2(:),y(:),20,'filled')
% 修饰一下
ax.FontName='cambria';
ax.LineWidth=1.5;
ax.GridLineStyle='--';
ax.XColor=[1,1,1].*.3;
ax.YColor=[1,1,1].*.3;
ax.ZColor=[1,1,1].*.3;
view(30,20)

以上就是python机器学习MATLAB最小二乘法的两种解读的详细内容，更多关于MATLAB最小二乘法解读的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • 最小二乘法及其python实现详解

    最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出).它通过最小化误差的平方和寻找数据的最佳函数匹配.利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小.最小二乘法还可用于曲线拟合.其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达. 那什么是最小二乘法呢?别着急,我们先从几个简单的概念说起. 假设我们现在有一系列的数据点 ,那么由我们给出的拟合函数h(x)得到的估计量就是

  • python中matplotlib实现最小二乘法拟合的过程详解

    python中matplotlib实现最小二乘法拟合的过程详解

    前言 最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出).它通过最小化误差的平方和寻找数据的最佳函数匹配.利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小.最小二乘法还可用于曲线拟合.其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达. 下面这篇文章主要跟大家介绍了关于python中matplotlib实现最小二乘法拟合的相关内容,下面话不多说,来一起看看详细的介绍:

  • python中最小二乘法详细讲解

    python中在实现一元线性回归时会使用最小二乘法,那你知道最小二乘法是什么吗.其实最小二乘法为分类回归算法的基础,从求解线性透视图中的消失点,m元n次函数的拟合,包括后来学到的神经网络,其思想归根结底全都是最小二乘法.本文向大家介绍python中的最小二乘法. 一.最小二乘法是什么 最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出). 二.最小二乘法实现原理 通过最小化误差的平方和寻找数据的最佳函数匹配. 三.最小二乘法功

  • Matlab制作视频并转换成gif动态图的两种方法

    一.第一个方法比较简单,就是使用movie(f)直接取生成AVI视频文件. %% f(t)-->f(4*t+12) 并且验证%% function Signal_change() tic%记录程序运行时间 figure n = 0; t = -2*pi:0.01:2*pi; y = sin(t);%周期为2*pi y_result = sin(4*t); plot(t,y,'b'); xlabel('t'); ylabel('Amplitude'); n = n+1; F(n) = getfra

  • python机器学习MATLAB最小二乘法的两种解读

    python机器学习MATLAB最小二乘法的两种解读

    目录 最小二乘法 代价函数与最小二乘法 向量到子空间的距离与最小二乘法 最小二乘法与多项式拟合 多项式拟合结果绘图: 最小二乘法与多元线性回归 多元线性回归结果绘图: 最小二乘法 大部分的最小二乘法公式推导,都是使用的 代价函数偏导 的方式来求得的,在这里首先展示如何通过代价函数求偏导的方式得到最小二乘公式,再展示李扬老师讲解的如何由向量到子空间的距离得来最小二乘法公式. 代价函数与最小二乘法 假设我们的拟合结果为: 则平方损失函数为: 平方损失函数的形式只有极小值,没有极大值,我们要使代价函数

  • Python在图片中添加文字的两种方法

    Python在图片中添加文字的两种方法

    本文主要介绍的是利用Python在图片中添加文字的两种方法,下面分享处理供大家参考学习,下来要看看吧 一.使用OpenCV 在图片中添加文字看上去很简单,但是如果是利用OpenCV来做却很麻烦.OpenCV中并没有使用自定义字体文件的函数,这不仅意味着我们不能使用自己的字体,而且意味着他无法显示中文字符.这还是非常要命的事情.而且他显示出来的文字位置也不太好控制.比如下面的代码,他想做的仅仅是显示数字3: 代码: #coding=utf-8 import cv2 import numpy as

  • python实现中文输出的两种方法

    本文实例讲述了python实现中文输出的两种方法.分享给大家供大家参考.具体如下: 方法一: 用encode和decode 如: import os.path import xlrd,sys Filename='/home/tom/Desktop/1234.xls' if not os.path.isfile(Filename): raise NameError,"%s is not a valid filename"%Filename bk=xlrd.open_workbook(Fi

  • Python生成MD5值的两种方法实例分析

    本文实例讲述了Python生成MD5值的两种方法.分享给大家供大家参考,具体如下: # -*- coding:utf-8 -*- import datetime # NO.1 使用MD5 import md5 src = 'this is a md5 test.' m1 = md5.new() m1.update(src) print m1.hexdigest() 运行结果: 174b086fc6358db6154bd951a8947837 # -*- coding:utf-8 -*- # NO

  • Python实现平行坐标图的两种方法小结

    平行坐标图,一种数据可视化的方式.以多个垂直平行的坐标轴表示多个维度,以维度上的刻度表示在该属性上对应值,相连而得的一个折线表示一个样本,以不同颜色区分类别. 但是很可惜,才疏学浅,没办法在Python里实现不同颜色来区分不同的类别.如果对此比较在意的大神可以不要往下看了......... 上图是一个基于iris数据集所画的一个平行坐标图. 隔开隔开.......................................隔开隔开 不多扯了,下面正式上代码 方法一.基于pyecharts第三

  • python生成requirements.txt的两种方法

    python项目如何在另一个环境上重新构建项目所需要的运行环境依赖包? 使用的时候边记载是个很麻烦的事情,总会出现遗漏的包的问题,这个时候手动安装也很麻烦,不能确定代码报错的需要安装的包是什么版本.这些问题,requirements.txt都可以解决! 生成requirements.txt,有两种方式: 第一种 适用于 单虚拟环境的情况: : pip freeze > requirements.txt 为什么只适用于单虚拟环境?因为这种方式,会将环境中的依赖包全都加入,如果使用的全局环境,则下载

  • 对Python中创建进程的两种方式以及进程池详解

    在Python中创建进程有两种方式,第一种是: from multiprocessing import Process import time def test(): while True: print('---test---') time.sleep(1) if __name__ == '__main__': p=Process(target=test) p.start() while True: print('---main---') time.sleep(1) 上面这段代码是在window

  • Python操作MySQL数据库的两种方式实例分析【pymysql和pandas】

    Python操作MySQL数据库的两种方式实例分析【pymysql和pandas】

    本文实例讲述了Python操作MySQL数据库的两种方式.分享给大家供大家参考,具体如下: 第一种 使用pymysql 代码如下: import pymysql #打开数据库连接 db=pymysql.connect(host='1.1.1.1',port=3306,user='root',passwd='123123',db='test',charset='utf8') cursor=db.cursor()#使用cursor()方法获取操作游标 sql = "select * from tes

  • python对象转字典的两种实现方式示例

    本文实例讲述了python对象转字典的两种实现方式.分享给大家供大家参考,具体如下: 一. 方便但不完美的__dict__ 对象转字典用到的方法为__dict__. 比如对象对象a的属性a.name='wk', a.age=18, 那么如果直接将使用a.__dict__获得对应的字典的值为: {name: 'wk', aget:18}, 很方便, 但是也存在一些限制. 其不完美之处在于: 比如: class A(object): name = 'wukt' age = 18 def __init

  • Python实现图片裁剪的两种方式(Pillow和OpenCV)

    在这篇文章里我们聊一下Python实现图片裁剪的两种方式,一种利用了Pillow,还有一种利用了OpenCV.两种方式都需要简单的几行代码,这可能也就是现在Python那么流行的原因吧. 首先,我们有一张原始图片,如下图所示: 原始图片 然后,我们利用OpenCV对其进行裁剪,代码如下所示: import cv2 img = cv2.imread("./data/cut/thor.jpg") print(img.shape) cropped = img[0:128, 0:512] #

随机推荐