C++详细讲解图论的基础与图的储存

目录

• 一、前言
• 二、图的定义
• 三、图的储存
• 1.邻接矩阵
• 2.邻接表
• 3.邻接矩阵与邻接表的优缺点对比

一、前言

在算法中一般都需要把问题抽象成图论问题然后用图论的算法解决问题。

图论涉及相当多的算法，包括图DFS和BFS、连通性、拓扑排序、最小生成树、最短路径、最大流网络、图的着色问题等等

图论算法在计算机科学中扮演着很重要的角色，它提供了对很多问题都有效的一种简单而系统的建模方式。很多问题都可以转化为图论问题，然后用图论的基本算法加以解决。

二、图的定义

图（graph）

如上图是一个图G，一个图由顶点（vertex）集V和边（edge）集E组成，即G=(V, E)，和树类似，其顶点又称为结点，并且边是有意义的，如上图(0,1)称为一条边。

上图中黑色的带数字的点就是顶点,可抽象成某个事物或对象。顶点之间的线就是边，表示事物与事物之间的关系。

需要注意的是在图论中边表示的是顶点之间的逻辑关系，粗细长短都无所谓的。包括上面的顶点也一样，表示逻辑事物或对象，画的时候大小形状都无所谓。

顶点（vertex）的属性：

度数（degree），与该顶点相关联的总边数，一个图G的总度数d(V)等于总边数2倍：2E。当图的边具有方向时，一个顶点又分为出度（out-degree）和入度（in-degree），出度是以该顶点为起点的边数，入度是以该顶点为终点的边数。

阶数（order），图G中顶点集V的大小为G的阶数。

边又称为线（line）或弧（arc），边(u,v)中表示u和v邻接（adjacent），(u, v) ∈ E，边（edge）的属性：

一条边是一个顶点对(u,v)，u, v ∈ V，按照图的顶点对是否有序，顶点对有序的图称为有向图（directed graph, digraph，此时边(u,v)和(v,u)是两条不同的边，顶点对无序的图称为无向图（undirected graph），此时边(u,v)和(v,u)是两条相同的边，无向图可看作一个特殊的有向图。

有向边： 有向边就是固定这一条边只能从x通往y，y通往x则不可以。

无向边 : 无向边就是一条边可以从x通往y，y也可以通往x。

自环边: 一条边的起点终点是一个点。

平行边： 两个顶点之间存在多条边相连接。

有权图： 权值就是一条边的长度或代价。

无权图： 不是边的权值为0，而是全都为1。

稀疏图: 每个顶点的度数较小的图，如下图：

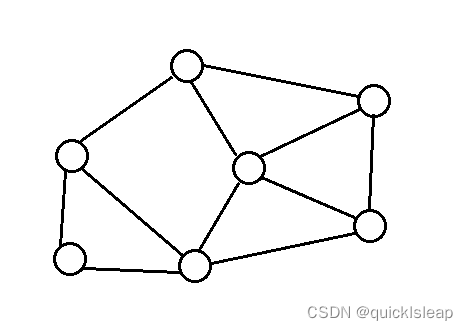
稠密图: 每个顶点的度数较大的图，如下图：

稀疏图：有很少条边或弧（边的条数|E|远小于|V|²）的图称为稀疏图（sparse graph）。

稠密图：有很多条边或弧 (边的条数|E|接近|V|²) 的图称为稠密图（dense graph）。 简单来说：我们假设某个图的点的个数 为 N, 边的个数为 M， 当 M << N ^ 2 (平方)（当边数远小于点的平方）时称为 稀疏图，当 M ≈ N ^ 2 （当边数约等于点的平方）时称为 稠密图， 如果图为稀疏图的时候，我们一般用邻接表储存，稠密图的时候，一般用邻接矩阵存储。

三、图的储存

那么，该怎么去储存图呢？

1.邻接矩阵

邻接矩阵是二维数据 ：例如，g[ ][ ] 时空间需求为V^2,这种存储方式适合存储稠密图

邻接矩阵每一位存的是一条边 行代表的是起始点 ,列代表的是终止点,而里面存的值就是这条边的权值

一个点到自己的距离是0，到没有直接边连接的点的权值是无穷大

需要注意的是，有向图与无向图的矩阵不同，对于无向图，当vi、vj之间由边，则a[i][j]=a[j][i]=1,但是有向图，若i指向j,只有a[i][j]=1,a[j][i]=0

邻接矩阵要初始化

如下：

for(int i = 1; i <= n1; i++)// n1 为数组第一维大小
    {
        for(int j =  1; j <= n2; j++)// n2 为数组第一维大小
        {
           g[i][j] = g[j][i] =  0 ;
        }
    }

也可以借助memset来快速地将一个数组中的所有元素都初始化为0。

上面的代码等价于：

memset(g, 0, sizeof(g));

注意，memset只能用来初始化0和 -1，并且需要加上头文件cstring。

cin>>n>>m;//n表示点的数量,m表示边的数量
for(int i = 1;i <= m; i++){//枚举输入边
    cin>>x>>y>>z;//如上描述
    dis[x][y] = z;    //有向边：
    dis[x][y] = dis[y][x] = z;    //无向边：
}

2.邻接表

又叫链式前向星，其实就是链表。邻接表的思想是，对于图中的每一个顶点，用一个数组来记录这个点和哪些点相连。

如果用邻接矩阵表示稀疏图就会浪费大量内存空间，而用链接表，则是通过把顶点所能到的顶点的边保存在链表中来表示图。

步骤

1.用 h 数组保存各个节点能到的第一个节点的编号。开始时，h[i] 全部为 -1。

2.用 e 数组保存节点编号，ne 数组保存 e 数组对应位置的下一个节点所在的索引。

3.用 idx 保存下一个 e 数组中，可以放入节点位置的索引

4.插入边使用的头插法，例如插入：a->b。首先把b节点存入e数组，e[idx] = b。然后 b 节点的后继是h[a]，ne[idx] = h[a]。最后，a 的后继更新为 b 节点的编号，h[a] = idx，索引指向下一个可以存储节点的位置，idx ++ 。

模板如下：

//邻接表
const int N = 100010, M = N * 2;
//无向图n条边时，最多2n个idx，因为每条边在邻接表中会出现两次
int h[N],  w[N], e[M], ne[M], idx;
//n个链表头，e每一个结点的值，ne每一个结点的next指针
// 添加一条边a->b
void add(int a, int b, int c)
{//e记录当前点的值(地址->值),ne下一点的地址(地址->地址)，h记录指向的第一个点的地址(值->地址)
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
// 初始化
idx = 0;
memset(h, -1, sizeof h);

3.邻接矩阵与邻接表的优缺点对比

空间方面：当图的顶点数很多、但是边的数量很少时，如果用邻接矩阵，我们就需要开一个很大的二维数组，最后我们需要存储 n*n 个数。但是用邻接表，最后我们存储的数据量只是边数的两倍。

效率方面：用邻接表存图的最大缺点就是随机访问效率低。比如，我们需要询问点 a 是否和点 b 连，我们就要遍历G[a]，检查这个vector里是否有 b 。而在邻接矩阵中，只需要根据G[a][b]就能判断。

邻接表可以记录重复边：如果两个点之间有多条边，用邻接矩阵只能记录一条，但是用邻接表就能记录多条。虽然重复的边看起来是多余的，但在很多时候对解题来说是必要的。

因此，我们需要对不同的应用情景选择不同的存图方法。

如果是稀疏图（顶点很多、边很少），一般用邻接表；

如果是稠密图（顶点很少、边很多），一般用邻接矩阵。

到此这篇关于C++详细讲解图论的基础与图的储存的文章就介绍到这了,更多相关C++图论内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！