Unity实现图形相交检测

前言

图形相交检测常常用在伤害判定，使用自定义的图形相交检测，可以在一定程度上控制性能。

比如2D格斗游戏中使用的矩形包围盒（AABB），一些动作游戏中常常出现的扇形攻击。

2D的图形相交检测能够满足大部分的需求，且可以拓展成为柱状的3D物体，2D比3D的计算复杂度会低很多，3D的图形检测原理与2D相似，本文会实现几个圆形与其他2D图形的相交检测：

1、圆形与圆形

2、圆形与胶囊体

3、圆形与扇形

4、圆形与凸多边形

5、圆形与AABB

6、圆形与OBB

通过简单化处理，把被判定物都处理成由圆柱或多个圆柱构成的区域，所以只需要考虑圆形与其他形状的相交。

圆形与圆形

两个圆形的相交检测非常简单直观，只需要判断半径只和与距离的大小。

定义圆形区间：

/// <summary>
/// 圆形区间
/// </summary>
public struct CircleArea
 {
 public Vector2 o;
 public float r;
 }

o ——圆心坐标

r  ——圆半径

相交判断：

/// <summary>
/// 判断圆形与圆形相交
/// </summary>
/// <param name="circleArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool Circle(CircleArea circleArea, CircleArea target)
 {
  return (circleArea.o - target.o).sqrMagnitude < (circleArea.r + target.r) * (circleArea.r + target.r);
 }

分离轴定理

分离轴定理（separating axis theorem, SAT）分离轴定理是指，两个不相交的凸集必然存在一个分离轴，使两个凸集在该轴上的投影是分离的。

判断两个形状是否相交，实际上是判断分离轴是否能把两个形状分离。若存在分离轴能使两个图形分离，则这两个图形是分离的。

基于以上理论，寻找分离轴是我们要做的工作，重新考虑两个圆形的相交检测，实际上我们做的是把圆心连线的方向作为分离轴：

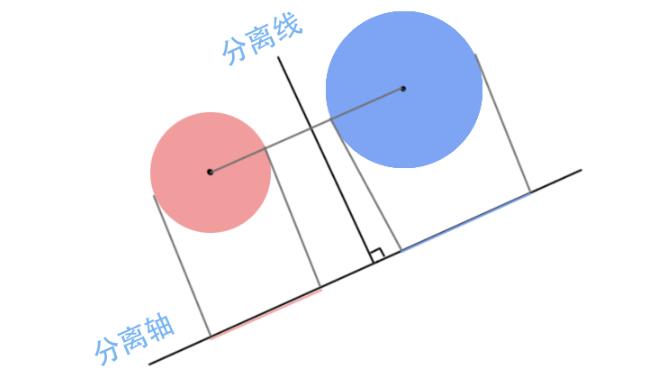
上图中两图形的投影在分离轴上是分离的，存在分离线将两者隔开,于是我们可以断定两图形是分离的。

胶囊体的本质

定义一个线段 u，距离 d。胶囊体实际上是与线段 u 的最短距离小于 d 的点的集合。判断一个点 x 处于胶囊体内部，就是判断点与线段的距离。

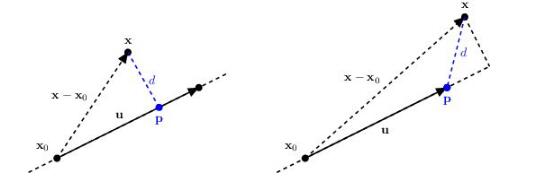
求点 x 与线段 u 最短距离的过程是:

1、求出点 x 在线段 u 所在直线上的投影点 P；

2、将投影点 P 限制在线段的范围内（如右图中投影点不在线段内，则限定到线段内）；

3、x 与 P 的距离即为所求；

/// <summary>
/// 线段与点的最短距离。
/// </summary>
/// <param name="x0">线段起点</param>
/// <param name="u">线段向量</param>
/// <param name="x">求解点</param>
/// <returns></returns>
public static float SqrDistanceBetweenSegmentAndPoint(Vector2 x0, Vector2 u, Vector2 x)
 {
 float t = Vector2.Dot(x - x0, u) / u.sqrMagnitude;
 return (x - (x0 + Mathf.Clamp01(t) * u)).sqrMagnitude;
 }

为避免开方计算，结果使用距离的平方。

圆形与胶囊体

分离轴是线段上距离圆心最近的点P与圆心所在方向。

定义胶囊体：

/// <summary>
/// 胶囊体
/// </summary>
 public struct CapsuleArea
 {
 public Vector2 X0;
 public Vector2 U;
 public float d;
 }

相交判断：

/// <summary>
/// 判断胶囊体与圆形相交
/// </summary>
/// <param name="capsuleArea"></param>
/// <param name="circleArea"></param>
/// <returns></returns>
public static bool Capsule(CapsuleArea capsuleArea, CircleArea circleArea)
 {
  float sqrD = SegmentPointSqrDistance(capsuleArea.X0, capsuleArea.U, circleArea.o);
  return sqrD < (circleArea.r + capsuleArea.d) * (circleArea.r + capsuleArea.d);
 }

圆形与扇形

当扇形角度大于180度时，就不再是凸多边形了，不能适用于分离轴理论。我们可以找出相交时圆心的所有可能区域，并把区域划分成可以简单验证的几个区域，逐个试验。

这里共划分了2个区间

1、半径为两者半径和的扇形区间，角度方向同扇形。验证方法是；验证距离与夹角。
2、扇形边为轴，圆形半径为大小组成的胶囊体空间，由于扇形的对称性，我们可以通过把圆心映射到一侧，从而只需要计算1条边。

定义扇形：

/// <summary>
/// 扇形区间。
/// </summary>
 public struct SectorArea
 {
  public Vector2 o;
  public float r;
  public Vector2 direction;
  public float angle;
 }

相交检测：

/// <summary>
/// 判断圆形与扇形相交。
/// </summary>
/// <param name="sectorArea"></param>
/// <param name="target"></param>
/// <returns></returns>
  public static bool Sector(SectorArea sectorArea, CircleArea target)
  {
   Vector2 tempDistance = target.o - sectorArea.o;
   float halfAngle = Mathf.Deg2Rad * sectorArea.angle / 2;
   if (tempDistance.sqrMagnitude < (sectorArea.r + target.r) * (sectorArea.r + target.r))
   {
    if (Vector3.Angle(tempDistance, sectorArea.direction) < sectorArea.angle / 2)
    {
     return true;
    }
    else
    {
     Vector2 targetInSectorAxis = new Vector2(Vector2.Dot(tempDistance,
      sectorArea.direction), Mathf.Abs(Vector2.Dot(tempDistance, new Vector2(-sectorArea.direction.y, sectorArea.direction.x))));
     Vector2 directionInSectorAxis = sectorArea.r * new Vector2(Mathf.Cos(halfAngle), Mathf.Sin(halfAngle));
     return SegmentPointSqrDistance(Vector2.zero, directionInSectorAxis, targetInSectorAxis) <= target.r * target.r;
    }
   }
   return false;
  }

圆形与凸多边形

定义多边形：

/// <summary>
/// 多边形区域。
/// </summary>
public struct PolygonArea
 {
  public Vector2[] vertexes;
 }

相交检测：

/// <summary>
/// 判断多边形与圆形相交
/// </summary>
/// <param name="polygonArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool PolygonS(PolygonArea polygonArea, CircleArea target)
  {
   if (polygonArea.vertexes.Length < 3)
   {
    Debug.Log("多边形边数小于3.");
    return false;
   }
   #region 定义临时变量
   //圆心
   Vector2 circleCenter = target.o;
   //半径的平方
   float sqrR = target.r * target.r;
   //多边形顶点
   Vector2[] polygonVertexes = polygonArea.vertexes;
   //圆心指向顶点的向量数组
   Vector2[] directionBetweenCenterAndVertexes = new Vector2[polygonArea.vertexes.Length];
   //多边形的边
   Vector2[] polygonEdges = new Vector2[polygonArea.vertexes.Length];
   for (int i = 0; i < polygonArea.vertexes.Length; i++)
   {
    directionBetweenCenterAndVertexes[i] = polygonVertexes[i] - circleCenter;
    polygonEdges[i] = polygonVertexes[i] - polygonVertexes[(i + 1)% polygonArea.vertexes.Length];
   }
   #endregion

   #region 以下为圆心处于多边形内的判断。
   //总夹角
   float totalAngle = Vector2.SignedAngle(directionBetweenCenterAndVertexes[polygonVertexes.Length - 1], directionBetweenCenterAndVertexes[0]);
   for (int i = 0; i < polygonVertexes.Length - 1; i++)
    totalAngle += Vector2.SignedAngle(directionBetweenCenterAndVertexes[i], directionBetweenCenterAndVertexes[i + 1]);
   if (Mathf.Abs(Mathf.Abs(totalAngle) - 360f) < 0.1f)
    return true;
   #endregion
   #region 以下为多边形的边与圆形相交的判断。
   for (int i = 0; i < polygonEdges.Length; i++)
    if (SegmentPointSqrDistance(polygonVertexes[i], polygonEdges[i], circleCenter) < sqrR)
     return true;
   #endregion
   return false;
  }

圆形与AABB

定义AABB：

/// <summary>
/// AABB区域
/// </summary>
public struct AABBArea
 {
  public Vector2 center;
  public Vector2 extents;
 }

AABB是凸多边形的特例，是长宽边分别与X/Y轴平行的矩形，这里我们要充分的利用他的对称性。

1 利用对称性将目标圆心映射到，以AABB中心为原点、两边为坐标轴的坐标系，的第一象限

2 将目标圆心映射到，以AABB第一象限角点为原点、两边为坐标轴的坐标系，的第一象限

3 最后只需要判断圆形半径与步骤2中映射点的向量大小

相交检测：

/// <summary>
/// 判断AABB与圆形相交
/// </summary>
/// <param name="aABBArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool AABB(AABBArea aABBArea, CircleArea target)
  {
   Vector2 v = Vector2.Max(aABBArea.center - target.o, -(aABBArea.center - target.o));
   Vector2 u = Vector2.Max(v - aABBArea.extents,Vector2.zero);
   return u.sqrMagnitude < target.r * target.r;
  }

圆形与OBB

定义OBB：

/// <summary>
/// OBB区域
/// </summary>
public struct OBBArea
 {
  public Vector2 center;
  public Vector2 extents;
  public float angle;
 }

OBB相对于AABB，矩形边不与坐标轴重合，对于它和圆形的相交检测只需要把圆形旋转到OBB边所在坐标系中，剩下的步骤与AABB的相同。

相交检测：

/// <summary>
/// 判断OBB与圆形相交
/// </summary>
/// <param name="oBBArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool OBB(OBBArea oBBArea, CircleArea target)
  {
   Vector2 p = oBBArea.center - target.o;
   p = Quaternion.AngleAxis(-oBBArea.angle, Vector3.forward) * p;
   Vector2 v = Vector2.Max(p, -p);
   Vector2 u = Vector2.Max(v - oBBArea.extents, Vector2.zero);
   return u.sqrMagnitude < target.r * target.r;
  }

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。