关于MD5算法原理与常用实现方式

目录

• 定义
• MD5特点
• 常见应用场景
• 1、校验文件的完整性
• 2、存储用户密码
• 原理
• 1、填补信息
• 2、拿到初始值
• 3、真正的计算
• MD5为什么不可逆
• java实现和使用

定义

MD全称Message-Digest，即信息摘要，所以MD家族的算法也叫信息摘要算法

MD家族有MD2、MD3、MD4、MD5，一代比一代强。

所以MD5是MD算法家族中，目前最常用的一种加密算法。

任何信息，都可以通过MD5算法运算生成一个16字节（128位）的散列值，但却无法通过这16个字节的散列值获得加密前的信息。

最终这16个散列值，通常用一个长度为32的十六进制字符串来表示。

这就是MD5最重要的一个特性：加密不可逆。

MD5特点

加密不可逆，即无法通过密文得到原文。

不变性，即相同的原文，通过MD5算法得到的密文总是相同的。

散列性，即对原文作轻微的改动，都可导致最终的密文完全改变。

常见应用场景

1、校验文件的完整性

如果张三给李四传了一个文件，如何确认这个文件传给李四是完整的呢

张三传文件前，先对文件做一个MD5加密，同时把MD5加密的密文传给李四

李四收到文件，也对该文件做MD5加密，如果得到的密文和张三给的密文一样，就说明文件是完整的。

2、存储用户密码

用户密码，理论上也不能直接明文存储在数据库中，因为一旦数据库被破解，用户的密码就全部丢失了

所以可以将用户密码做一个MD5加密，然后将密文存在数据库中

用户登录的时候，可以将用户的密码进行MD5加密，然后比对密文和数据库中的密文是否一致，来判断用户前台填的密码是否正确。

这只是一个思路，一般不会这么简单，一般生产环境会对用户密码加盐加密等等的处理，用户信息更加重要的，则需要更加复杂的计算逻辑。

原理

MD5的加密过程，整体来看，就是先定义四个值，然后用这四个值，对原文信息进行计算，并得到新的四个值，然后再对原文进行计算，再得到新的四个值，如此循环一定次数，最终对最后的这四个值进行简单的字符串拼接，就得到了最终的密文。

主要就是下面这3步：

1、填补信息

用原文长度位数对512求余，如果结果不为448，就填充到448位。填充是第一位填1，后面填0。512-448=64，用这剩余的64位，记录原文长度。

最终得到一个填补完的信息（总长=原文长度+512位）

2、拿到初始值

四个初始值，是MD5这个算法提前定义好的，分别是4个32位的值，总共刚好128位。

我们用ABCD命名：

• A=0x01234567
• B=0x89ABCDEF
• C=0xFEDCBA98
• D=0x76543210

3、真正的计算

计算分为多次循环，每次循环，都是用ABCD和原文在第一步填补完的信息，进行计算，最终得到新的ABCD。最后将最后一次ABCD拼成字符串，就是最终的密文。

• 循环先分为主循环，每个主循环中又套有子循环。
• 主循环次数 = 原文长度/512。
• 子循环次数 = 64次。

我们看看单次子循环都做了什么：

下面是单次子循环真正的计算逻辑（这段实现摘自网友）：

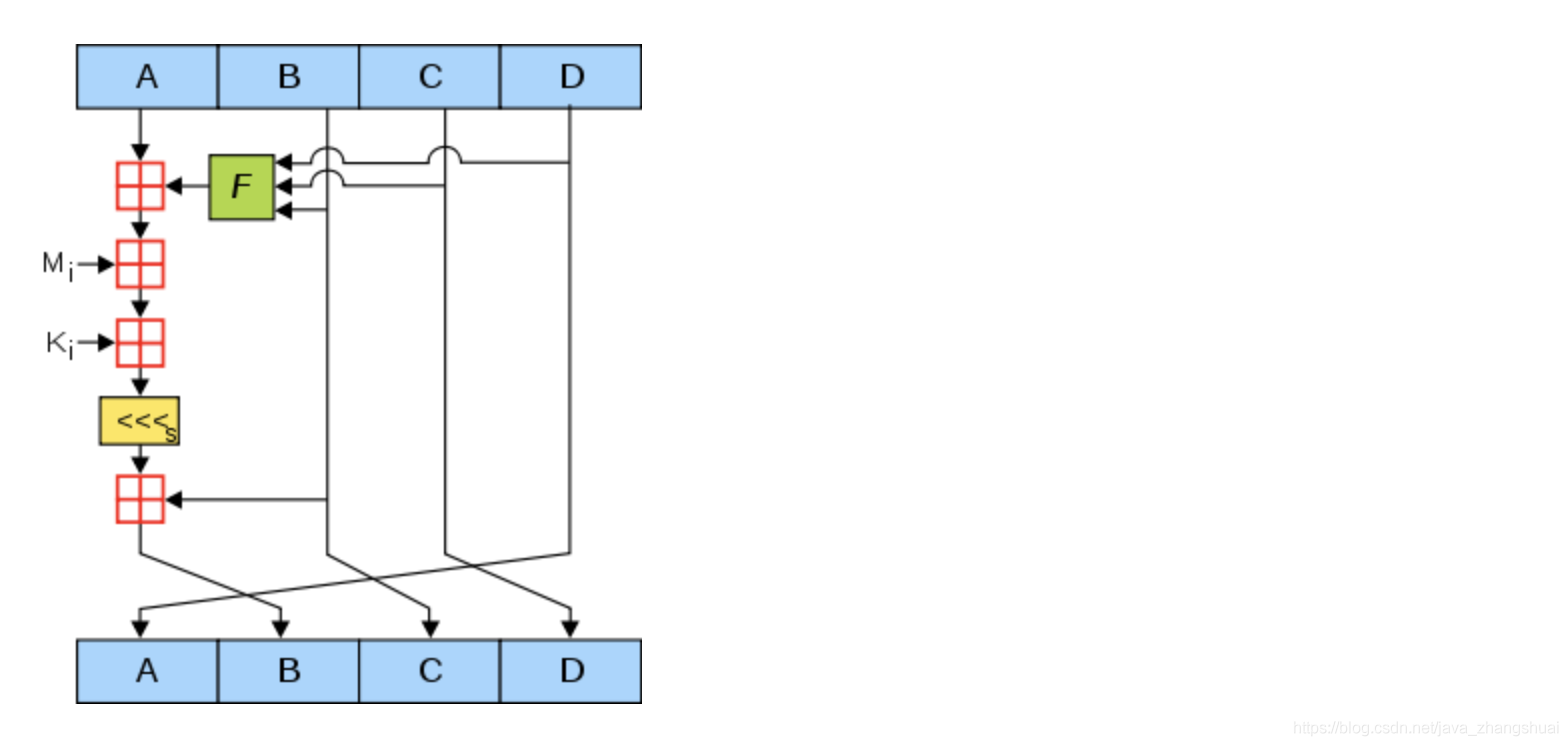
图中，A，B，C，D就是哈希值的四个分组。每一次循环都会让旧的ABCD产生新的ABCD。一共进行多少次循环呢？由处理后的原文长度决定。

• 假设处理后的原文长度是M
• 主循环次数 = M / 512
• 每个主循环中包含 512 / 32 * 4 = 64 次 子循环。

上面这张图所表达的就是单次子循环的流程。

下面对图中其他元素一一解释：

1.绿色F

图中的绿色F，代表非线性函数。官方MD5所用到的函数有四种：

F(X, Y, Z) =(X&Y) | ((~X) & Z)
G(X, Y, Z) =(X&Z) | (Y & (~Z))
H(X, Y, Z) =X^Y^Z
I(X, Y, Z)=Y^(X|(~Z))

在主循环下面64次子循环中，F、G、H、I 交替使用，第一个16次使用F，第二个16次使用G，第三个16次使用H，第四个16次使用I。

2.红色“田”字

很简单，红色的田字代表相加的意思。

3.Mi

Mi是第一步处理后的原文。在第一步中，处理后原文的长度是512的整数倍。把原文的每512位再分成16等份，命名为M0 ~ M15，每一等份长度32。在64次子循环中，每16次循环，都会交替用到M1 ~ M16之一。

4.Ki

一个常量，在64次子循环中，每一次用到的常量都是不同的。

5.黄色的<<

FF(a,b,c,d,Mj,s,ti)表示a=b+((a+F(b,c,d)+Mj+ti)<<<s)

<<<s表示循环左移s位

第一轮
 a=FF(a,b,c,d,M0,7,0xd76aa478)
 b=FF(d,a,b,c,M1,12,0xe8c7b756)
 c=FF(c,d,a,b,M2,17,0x242070db)
 d=FF(b,c,d,a,M3,22,0xc1bdceee)
 a=FF(a,b,c,d,M4,7,0xf57c0faf)
 b=FF(d,a,b,c,M5,12,0x4787c62a)
 c=FF(c,d,a,b,M6,17,0xa8304613)
 d=FF(b,c,d,a,M7,22,0xfd469501)
 a=FF(a,b,c,d,M8,7,0x698098d8)
 b=FF(d,a,b,c,M9,12,0x8b44f7af)
 c=FF(c,d,a,b,M10,17,0xffff5bb1)
 d=FF(b,c,d,a,M11,22,0x895cd7be)
 a=FF(a,b,c,d,M12,7,0x6b901122)
 b=FF(d,a,b,c,M13,12,0xfd987193)
 c=FF(c,d,a,b,M14,17,0xa679438e)
 d=FF(b,c,d,a,M15,22,0x49b40821)

第二轮
 a=GG(a,b,c,d,M1,5,0xf61e2562)
 b=GG(d,a,b,c,M6,9,0xc040b340)
 c=GG(c,d,a,b,M11,14,0x265e5a51)
 d=GG(b,c,d,a,M0,20,0xe9b6c7aa)
 a=GG(a,b,c,d,M5,5,0xd62f105d)
 b=GG(d,a,b,c,M10,9,0x02441453)
 c=GG(c,d,a,b,M15,14,0xd8a1e681)
 d=GG(b,c,d,a,M4,20,0xe7d3fbc8)
 a=GG(a,b,c,d,M9,5,0x21e1cde6)
 b=GG(d,a,b,c,M14,9,0xc33707d6)
 c=GG(c,d,a,b,M3,14,0xf4d50d87)
 d=GG(b,c,d,a,M8,20,0x455a14ed)
 a=GG(a,b,c,d,M13,5,0xa9e3e905)
 b=GG(d,a,b,c,M2,9,0xfcefa3f8)
 c=GG(c,d,a,b,M7,14,0x676f02d9)
 d=GG(b,c,d,a,M12,20,0x8d2a4c8a)

第三轮
 a=HH(a,b,c,d,M5,4,0xfffa3942)
 b=HH(d,a,b,c,M8,11,0x8771f681)
 c=HH(c,d,a,b,M11,16,0x6d9d6122)
 d=HH(b,c,d,a,M14,23,0xfde5380c)
 a=HH(a,b,c,d,M1,4,0xa4beea44)
 b=HH(d,a,b,c,M4,11,0x4bdecfa9)
 c=HH(c,d,a,b,M7,16,0xf6bb4b60)
 d=HH(b,c,d,a,M10,23,0xbebfbc70)
 a=HH(a,b,c,d,M13,4,0x289b7ec6)
 b=HH(d,a,b,c,M0,11,0xeaa127fa)
 c=HH(c,d,a,b,M3,16,0xd4ef3085)
 d=HH(b,c,d,a,M6,23,0x04881d05)
 a=HH(a,b,c,d,M9,4,0xd9d4d039)
 b=HH(d,a,b,c,M12,11,0xe6db99e5)
 c=HH(c,d,a,b,M15,16,0x1fa27cf8)
 d=HH(b,c,d,a,M2,23,0xc4ac5665)

第四轮
 a=II(a,b,c,d,M0,6,0xf4292244)
 b=II(d,a,b,c,M7,10,0x432aff97)
 c=II(c,d,a,b,M14,15,0xab9423a7)
 d=II(b,c,d,a,M5,21,0xfc93a039)
 a=II(a,b,c,d,M12,6,0x655b59c3)
 b=II(d,a,b,c,M3,10,0x8f0ccc92)
 c=II(c,d,a,b,M10,15,0xffeff47d)
 d=II(b,c,d,a,M1,21,0x85845dd1)
 a=II(a,b,c,d,M8,6,0x6fa87e4f)
 b=II(d,a,b,c,M15,10,0xfe2ce6e0)
 c=II(c,d,a,b,M6,15,0xa3014314)
 d=II(b,c,d,a,M13,21,0x4e0811a1)
 a=II(a,b,c,d,M4,6,0xf7537e82)
 b=II(d,a,b,c,M11,10,0xbd3af235)
 c=II(c,d,a,b,M2,15,0x2ad7d2bb)
 d=II(b,c,d,a,M9,21,0xeb86d391)

MD5为什么不可逆

MD5不可逆的原因，从原理上来看，

• 第一是他使用了散列函数，即上面的FGHI函数。
• 第二是他在里面用了大量的移位操作，即<<<，这些是不可逆的

比如有10110011，我们左移三位，变成了10011000，高三位的101被顶了，低三位用0代替了，那此时就绝对不可能用10011000再逆向得到10110011了。

java实现和使用

public class MD5Util {
    public static void main(String[] args) throws IOException {
        System.out.println(encodeString("123"));
    }
    public static String encodeString(String plainText) throws UnsupportedEncodingException {
        return encodeBytes(plainText.getBytes("UTF-8"));
    }
    public static String encodeBytes(byte[] bytes) {
        try {
            MessageDigest md = MessageDigest.getInstance("MD5");
            md.update(bytes);
            byte b[] = md.digest();
            int i;
            StringBuffer buf = new StringBuffer("");
            for (int offset = 0; offset < b.length; offset++) {
                i = b[offset];
                if (i < 0) {
                    i += 256;
                }
                if (i < 16) {
                    buf.append("0");
                }
                buf.append(Integer.toHexString(i));
            }
            return buf.toString();
        } catch (Exception e) {
            e.printStackTrace();
        }
        return "";
    }
}

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。