Python利用keras接口实现深度神经网络回归

目录

• 1 写在前面
• 2 代码分解介绍
• 2.1 准备工作
• 2.2 参数配置
• 2.3 数据导入与数据划分
• 2.4 联合分布图绘制
• 2.5 因变量分离与数据标准化
• 2.6 原有模型删除
• 2.7 最优Epoch保存与读取
• 2.8 模型构建
• 2.9 训练图像绘制
• 2.10 最优Epoch选取
• 2.11 模型测试、拟合图像绘制、精度验证与模型参数与结果保存
• 3 完整代码

1 写在前面

前期一篇文章Python TensorFlow深度学习回归代码：DNNRegressor详细介绍了基于TensorFlow tf.estimator接口的深度学习网络；而在TensorFlow 2.0中，新的Keras接口具有与 tf.estimator接口一致的功能，且其更易于学习，对于新手而言友好程度更高；在TensorFlow官网也建议新手从Keras接口入手开始学习。因此，本文结合TensorFlow Keras接口，加以深度学习回归的详细介绍与代码实战。

和上述博客类似，本文第二部分为代码的分解介绍，第三部分为完整代码。一些在上述博客介绍过的内容，在本文中就省略了，大家如果有需要可以先查看上述文章Python TensorFlow深度学习回归代码：DNNRegressor。

相关版本信息：Python版本：3.8.5；TensorFlow版本：2.4.1；编译器版本：Spyder 4.1.5。

2 代码分解介绍

2.1 准备工作

首先需要引入相关的库与包。

import os
import glob
import openpyxl
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
import scipy.stats as stats
import matplotlib.pyplot as plt
from sklearn import metrics
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers
from tensorflow.keras.callbacks import ModelCheckpoint
from tensorflow.keras.layers.experimental import preprocessing

由于后续代码执行过程中，会有很多数据的展示与输出，其中多数数据都带有小数部分；为了让程序所显示的数据更为整齐、规范，我们可以对代码的浮点数、数组与NumPy对象对应的显示规则加以约束。

np.set_printoptions(precision=4,suppress=True)

其中，precision设置小数点后显示的位数，默认为8；suppress表示是否使用定点计数法（即与科学计数法相对）。

2.2 参数配置

深度学习代码一大特点即为具有较多的参数需要我们手动定义。为避免调参时上下翻找，我们可以将主要的参数集中在一起，方便我们后期调整。

其中，具体参数的含义在本文后续部分详细介绍。

# Input parameters.
DataPath="G:/CropYield/03_DL/00_Data/AllDataAll.csv"
ModelPath="G:/CropYield/03_DL/02_DNNModle"
CheckPointPath="G:/CropYield/03_DL/02_DNNModle/Weights"
CheckPointName=CheckPointPath+"/Weights_{epoch:03d}_{val_loss:.4f}.hdf5"
ParameterPath="G:/CropYield/03_DL/03_OtherResult/ParameterResult.xlsx"
TrainFrac=0.8
RandomSeed=np.random.randint(low=21,high=22)
CheckPointMethod='val_loss'
HiddenLayer=[64,128,256,512,512,1024,1024]
RegularizationFactor=0.0001
ActivationMethod='relu'
DropoutValue=[0.5,0.5,0.5,0.3,0.3,0.3,0.2]
OutputLayerActMethod='linear'
LossMethod='mean_absolute_error'
LearnRate=0.005
LearnDecay=0.0005
FitEpoch=500
BatchSize=9999
ValFrac=0.2
BestEpochOptMethod='adam'

2.3 数据导入与数据划分

我的数据已经保存在了.csv文件中，因此可以用pd.read_csv直接读取。

其中，数据的每一列是一个特征，每一行是全部特征与因变量（就是下面的Yield）组合成的样本。

# Fetch and divide data.
MyData=pd.read_csv(DataPath,names=['EVI0610','EVI0626','EVI0712','EVI0728','EVI0813','EVI0829',
                                   'EVI0914','EVI0930','EVI1016','Lrad06','Lrad07','Lrad08',
                                   'Lrad09','Lrad10','Prec06','Prec07','Prec08','Prec09',
                                   'Prec10','Pres06','Pres07','Pres08','Pres09','Pres10',
                                   'SIF161','SIF177','SIF193','SIF209','SIF225','SIF241',
                                   'SIF257','SIF273','SIF289','Shum06','Shum07','Shum08',
                                   'Shum09','Shum10','SoilType','Srad06','Srad07','Srad08',
                                   'Srad09','Srad10','Temp06','Temp07','Temp08','Temp09',
                                   'Temp10','Wind06','Wind07','Wind08','Wind09','Wind10',
                                   'Yield'],header=0)

随后，对导入的数据划分训练集与测试集。

TrainData=MyData.sample(frac=TrainFrac,random_state=RandomSeed)
TestData=MyData.drop(TrainData.index)

其中，TrainFrac为训练集（包括验证数据）所占比例，RandomSeed为随即划分数据时所用的随机数种子。

2.4 联合分布图绘制

在开始深度学习前，我们可以分别对输入数据的不同特征与因变量的关系加以查看。绘制联合分布图就是一种比较好的查看多个变量之间关系的方法。我们用seaborn来实现这一过程。seaborn是一个基于matplotlib的Python数据可视化库，使得我们可以通过较为简单的操作，绘制出动人的图片。代码如下：

# Draw the joint distribution image.
def JointDistribution(Factors):
    plt.figure(1)
    sns.pairplot(TrainData[Factors],kind='reg',diag_kind='kde')
    sns.set(font_scale=2.0)
    DataDistribution=TrainData.describe().transpose()

# Draw the joint distribution image.
JointFactor=['Lrad07','Prec06','SIF161','Shum06','Srad07','Srad08','Srad10','Temp06','Yield']
JointDistribution(JointFactor)

其中，JointFactor为需要绘制联合分布图的特征名称，JointDistribution函数中的kind表示联合分布图中非对角线图的类型，可选'reg'与'scatter'、'kde'、'hist'，'reg'代表在图片中加入一条拟合直线，'scatter'就是不加入这条直线,'kde'是等高线的形式，'hist'就是类似于栅格地图的形式；diag_kind表示联合分布图中对角线图的类型，可选'hist'与'kde'，'hist'代表直方图，'kde'代表直方图曲线化。font_scale是图中的字体大小。JointDistribution函数中最后一句是用来展示TrainData中每一项特征数据的统计信息，包括最大值、最小值、平均值、分位数等。

图片绘制的示例如下：

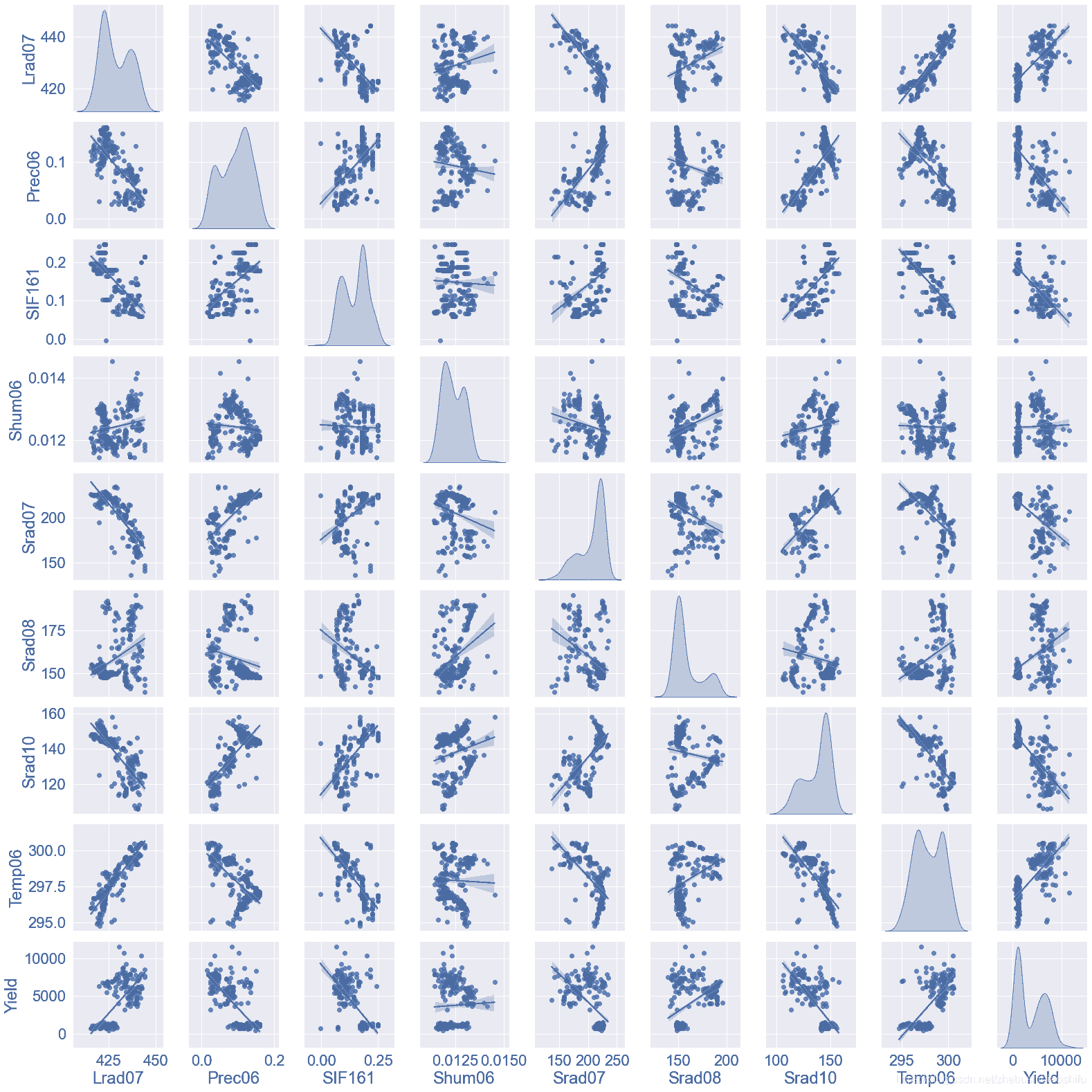
要注意，绘制联合分布图比较慢，建议大家不要选取太多的变量，否则程序会卡在这里比较长的时间。

2.5 因变量分离与数据标准化

因变量分离我们就不再多解释啦；接下来，我们要知道，对于机器学习、深度学习而言，数据标准化是十分重要的——用官网所举的一个例子：不同的特征在神经网络中会乘以相同的权重weight，因此输入数据的尺度（即数据不同特征之间的大小关系）将会影响到输出数据与梯度的尺度；因此，数据标准化可以使得模型更加稳定。

在这里，首先说明数据标准化与归一化的区别。

标准化即将训练集中某列的值缩放成均值为0，方差为1的状态；而归一化是将训练集中某列的值缩放到0和1之间。而在机器学习中，标准化较之归一化通常具有更高的使用频率，且标准化后的数据在神经网络训练时，其收敛将会更快。

最后，一定要记得——标准化时只需要对训练集数据加以处理，不要把测试集Test的数据引入了！因为标准化只需要对训练数据加以处理，引入测试集反而会影响标准化的作用。

# Separate independent and dependent variables.
TrainX=TrainData.copy(deep=True)
TestX=TestData.copy(deep=True)
TrainY=TrainX.pop('Yield')
TestY=TestX.pop('Yield')

# Standardization data.
Normalizer=preprocessing.Normalization()
Normalizer.adapt(np.array(TrainX))

在这里，我们直接运用preprocessing.Normalization()建立一个预处理层，其具有数据标准化的功能；随后，通过.adapt()函数将需要标准化的数据（即训练集的自变量）放入这一层，便可以实现数据的标准化操作。

2.6 原有模型删除

我们的程序每执行一次，便会在指定路径中保存当前运行的模型。为保证下一次模型保存时不受上一次模型运行结果干扰，我们可以将模型文件夹内的全部文件删除。

# Delete the model result from the last run.
def DeleteOldModel(ModelPath):
    AllFileName=os.listdir(ModelPath)
    for i in AllFileName:
        NewPath=os.path.join(ModelPath,i)
        if os.path.isdir(NewPath):
            DeleteOldModel(NewPath)
        else:
            os.remove(NewPath)

# Delete the model result from the last run.
DeleteOldModel(ModelPath)

这一部分的代码在文章Python TensorFlow深度学习回归代码：DNNRegressor有详细的讲解，这里就不再重复。

2.7 最优Epoch保存与读取

在我们训练模型的过程中，会让模型运行几百个Epoch（一个Epoch即全部训练集数据样本均进入模型训练一次）；而由于每一次的Epoch所得到的精度都不一样，那么我们自然需要挑出几百个Epoch中最优秀的那一个Epoch。

# Find and save optimal epoch.
def CheckPoint(Name):
    Checkpoint=ModelCheckpoint(Name,
                               monitor=CheckPointMethod,
                               verbose=1,
                               save_best_only=True,
                               mode='auto')
    CallBackList=[Checkpoint]
    return CallBackList

# Find and save optimal epochs.
CallBack=CheckPoint(CheckPointName)

其中，Name就是保存Epoch的路径与文件名命名方法；monitor是我们挑选最优Epoch的依据，在这里我们用验证集数据对应的误差来判断这个Epoch是不是我们想要的；verbose用来设置输出日志的内容，我们用1就好；save_best_only用来确定我们是否只保存被认定为最优的Epoch；mode用以判断我们的monitor是越大越好还是越小越好，前面提到了我们的monitor是验证集数据对应的误差，那么肯定是误差越小越好，所以这里可以用'auto'或'min'，其中'auto'是模型自己根据用户选择的monitor方法来判断越大越好还是越小越好。

找到最优Epoch后，将其传递给CallBack。需要注意的是，这里的最优Epoch是多个Epoch——因为每一次Epoch只要获得了当前模型所遇到的最优解，它就会保存；下一次再遇见一个更好的解时，同样保存，且不覆盖上一次的Epoch。可以这么理解，假如一共有三次Epoch，所得到的误差分别为5，7，4；那么我们保存的Epoch就是第一次和第三次。

2.8 模型构建

Keras接口下的模型构建就很清晰明了了。相信大家在看了前期一篇文章Python TensorFlow深度学习回归代码：DNNRegressor后，结合代码旁的注释就理解啦。

# Build DNN model.
def BuildModel(Norm):
    Model=keras.Sequential([Norm, # 数据标准化层

                            layers.Dense(HiddenLayer[0], # 指定隐藏层1的神经元个数
                                         kernel_regularizer=regularizers.l2(RegularizationFactor), # 运用L2正则化
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(), # 引入LeakyReLU这一改良的ReLU激活函数，从而加快模型收敛，减少过拟合
                            layers.BatchNormalization(), # 引入Batch Normalizing，加快网络收敛与增强网络稳固性
                            layers.Dropout(DropoutValue[0]), # 指定隐藏层1的Dropout值

                            layers.Dense(HiddenLayer[1],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[1]),

                            layers.Dense(HiddenLayer[2],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[2]),

                            layers.Dense(HiddenLayer[3],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[3]),

                            layers.Dense(HiddenLayer[4],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[4]),

                            layers.Dense(HiddenLayer[5],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[5]),

                            layers.Dense(HiddenLayer[6],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            # If batch normalization is set in the last hidden layer, the error image
                            # will show a trend of first stable and then decline; otherwise, it will
                            # decline and then stable.
                            # layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[6]),

                            layers.Dense(units=1,
                                         activation=OutputLayerActMethod)]) # 最后一层就是输出层
    Model.compile(loss=LossMethod, # 指定每个批次训练误差的减小方法
                  optimizer=tf.keras.optimizers.Adam(learning_rate=LearnRate,decay=LearnDecay))
                  # 运用学习率下降的优化方法
    return Model

# Build DNN regression model.
DNNModel=BuildModel(Normalizer)
DNNModel.summary()
DNNHistory=DNNModel.fit(TrainX,
                        TrainY,
                        epochs=FitEpoch,
                        # batch_size=BatchSize,
                        verbose=1,
                        callbacks=CallBack,
                        validation_split=ValFrac)

在这里，.summary()查看模型摘要，validation_split为在训练数据中，取出ValFrac所指定比例的一部分作为验证数据。DNNHistory则记录了模型训练过程中的各类指标变化情况，接下来我们可以基于其绘制模型训练过程的误差变化图像。

2.9 训练图像绘制

机器学习中，过拟合是影响训练精度的重要因素。因此，我们最好在训练模型的过程中绘制训练数据、验证数据的误差变化图象，从而更好获取模型的训练情况。

# Draw error image.
def LossPlot(History):
    plt.figure(2)
    plt.plot(History.history['loss'],label='loss')
    plt.plot(History.history['val_loss'],label='val_loss')
    plt.ylim([0,4000])
    plt.xlabel('Epoch')
    plt.ylabel('Error')
    plt.legend()
    plt.grid(True)

# Draw error image.
LossPlot(DNNHistory)

其中，'loss'与'val_loss'分别是模型训练过程中，训练集、验证集对应的误差；如果训练集误差明显小于验证集误差，就说明模型出现了过拟合。

2.10 最优Epoch选取

前面提到了，我们将多个符合要求的Epoch保存在了指定的路径下，那么最终我们可以从中选取最好的那个Epoch，作为模型的最终参数，从而对测试集数据加以预测。那么在这里，我们需要将这一全局最优Epoch选取出，并带入到最终的模型里。

# Optimize the model based on optimal epoch.
def BestEpochIntoModel(Path,Model):
    EpochFile=glob.glob(Path+'/*')
    BestEpoch=max(EpochFile,key=os.path.getmtime)
    Model.load_weights(BestEpoch)
    Model.compile(loss=LossMethod,
                  optimizer=BestEpochOptMethod)
    return Model

# Optimize the model based on optimal epoch.
DNNModel=BestEpochIntoModel(CheckPointPath,DNNModel）

总的来说，这里就是运用了os.path.getmtime模块，将我们存储Epoch的文件夹中最新的那个Epoch挑出来——这一Epoch就是使得验证集数据误差最小的全局最优Epoch；并通过load_weights将这一Epoch对应的模型参数引入模型。

2.11 模型测试、拟合图像绘制、精度验证与模型参数与结果保存

前期一篇文章Python TensorFlow深度学习回归代码：DNNRegressor中有相关的代码讲解内容，因此这里就不再赘述啦。

# Draw Test image.
def TestPlot(TestY,TestPrediction):
    plt.figure(3)
    ax=plt.axes(aspect='equal')
    plt.scatter(TestY,TestPrediction)
    plt.xlabel('True Values')
    plt.ylabel('Predictions')
    Lims=[0,10000]
    plt.xlim(Lims)
    plt.ylim(Lims)
    plt.plot(Lims,Lims)
    plt.grid(False)

# Verify the accuracy and draw error hist image.
def AccuracyVerification(TestY,TestPrediction):
    DNNError=TestPrediction-TestY
    plt.figure(4)
    plt.hist(DNNError,bins=30)
    plt.xlabel('Prediction Error')
    plt.ylabel('Count')
    plt.grid(False)
    Pearsonr=stats.pearsonr(TestY,TestPrediction)
    R2=metrics.r2_score(TestY,TestPrediction)
    RMSE=metrics.mean_squared_error(TestY,TestPrediction)**0.5
    print('Pearson correlation coefficient is {0}, and RMSE is {1}.'.format(Pearsonr[0],RMSE))
    return (Pearsonr[0],R2,RMSE)

# Save key parameters.
def WriteAccuracy(*WriteVar):
    ExcelData=openpyxl.load_workbook(WriteVar[0])
    SheetName=ExcelData.get_sheet_names()
    WriteSheet=ExcelData.get_sheet_by_name(SheetName[0])
    WriteSheet=ExcelData.active
    MaxRowNum=WriteSheet.max_row
    for i in range(len(WriteVar)-1):
        exec("WriteSheet.cell(MaxRowNum+1,i+1).value=WriteVar[i+1]")
    ExcelData.save(WriteVar[0])

# Predict test set data.
TestPrediction=DNNModel.predict(TestX).flatten()

# Draw Test image.
TestPlot(TestY,TestPrediction)

# Verify the accuracy and draw error hist image.
AccuracyResult=AccuracyVerification(TestY,TestPrediction)
PearsonR,R2,RMSE=AccuracyResult[0],AccuracyResult[1],AccuracyResult[2]

# Save model and key parameters.
DNNModel.save(ModelPath)
WriteAccuracy(ParameterPath,PearsonR,R2,RMSE,TrainFrac,RandomSeed,CheckPointMethod,
              ','.join('%s' %i for i in HiddenLayer),RegularizationFactor,
              ActivationMethod,','.join('%s' %i for i in DropoutValue),OutputLayerActMethod,
              LossMethod,LearnRate,LearnDecay,FitEpoch,BatchSize,ValFrac,BestEpochOptMethod)

得到拟合图像如下：

得到误差分布直方图如下：

至此，代码的分解介绍就结束啦~

3 完整代码

# -*- coding: utf-8 -*-
"""
Created on Tue Feb 24 12:42:17 2021

@author: fkxxgis
"""

import os
import glob
import openpyxl
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
import scipy.stats as stats
import matplotlib.pyplot as plt
from sklearn import metrics
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers
from tensorflow.keras.callbacks import ModelCheckpoint
from tensorflow.keras.layers.experimental import preprocessing

np.set_printoptions(precision=4,suppress=True)

# Draw the joint distribution image.
def JointDistribution(Factors):
    plt.figure(1)
    sns.pairplot(TrainData[Factors],kind='reg',diag_kind='kde')
    sns.set(font_scale=2.0)
    DataDistribution=TrainData.describe().transpose()

# Delete the model result from the last run.
def DeleteOldModel(ModelPath):
    AllFileName=os.listdir(ModelPath)
    for i in AllFileName:
        NewPath=os.path.join(ModelPath,i)
        if os.path.isdir(NewPath):
            DeleteOldModel(NewPath)
        else:
            os.remove(NewPath)

# Find and save optimal epoch.
def CheckPoint(Name):
    Checkpoint=ModelCheckpoint(Name,
                               monitor=CheckPointMethod,
                               verbose=1,
                               save_best_only=True,
                               mode='auto')
    CallBackList=[Checkpoint]
    return CallBackList

# Build DNN model.
def BuildModel(Norm):
    Model=keras.Sequential([Norm, # 数据标准化层

                            layers.Dense(HiddenLayer[0], # 指定隐藏层1的神经元个数
                                         kernel_regularizer=regularizers.l2(RegularizationFactor), # 运用L2正则化
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(), # 引入LeakyReLU这一改良的ReLU激活函数，从而加快模型收敛，减少过拟合
                            layers.BatchNormalization(), # 引入Batch Normalizing，加快网络收敛与增强网络稳固性
                            layers.Dropout(DropoutValue[0]), # 指定隐藏层1的Dropout值

                            layers.Dense(HiddenLayer[1],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[1]),

                            layers.Dense(HiddenLayer[2],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[2]),

                            layers.Dense(HiddenLayer[3],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[3]),

                            layers.Dense(HiddenLayer[4],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[4]),

                            layers.Dense(HiddenLayer[5],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[5]),

                            layers.Dense(HiddenLayer[6],
                                         kernel_regularizer=regularizers.l2(RegularizationFactor),
                                         # activation=ActivationMethod
                                         ),
                            layers.LeakyReLU(),
                            # If batch normalization is set in the last hidden layer, the error image
                            # will show a trend of first stable and then decline; otherwise, it will
                            # decline and then stable.
                            # layers.BatchNormalization(),
                            layers.Dropout(DropoutValue[6]),

                            layers.Dense(units=1,
                                         activation=OutputLayerActMethod)]) # 最后一层就是输出层
    Model.compile(loss=LossMethod, # 指定每个批次训练误差的减小方法
                  optimizer=tf.keras.optimizers.Adam(learning_rate=LearnRate,decay=LearnDecay))
                  # 运用学习率下降的优化方法
    return Model

# Draw error image.
def LossPlot(History):
    plt.figure(2)
    plt.plot(History.history['loss'],label='loss')
    plt.plot(History.history['val_loss'],label='val_loss')
    plt.ylim([0,4000])
    plt.xlabel('Epoch')
    plt.ylabel('Error')
    plt.legend()
    plt.grid(True)

# Optimize the model based on optimal epoch.
def BestEpochIntoModel(Path,Model):
    EpochFile=glob.glob(Path+'/*')
    BestEpoch=max(EpochFile,key=os.path.getmtime)
    Model.load_weights(BestEpoch)
    Model.compile(loss=LossMethod,
                  optimizer=BestEpochOptMethod)
    return Model

# Draw Test image.
def TestPlot(TestY,TestPrediction):
    plt.figure(3)
    ax=plt.axes(aspect='equal')
    plt.scatter(TestY,TestPrediction)
    plt.xlabel('True Values')
    plt.ylabel('Predictions')
    Lims=[0,10000]
    plt.xlim(Lims)
    plt.ylim(Lims)
    plt.plot(Lims,Lims)
    plt.grid(False)

# Verify the accuracy and draw error hist image.
def AccuracyVerification(TestY,TestPrediction):
    DNNError=TestPrediction-TestY
    plt.figure(4)
    plt.hist(DNNError,bins=30)
    plt.xlabel('Prediction Error')
    plt.ylabel('Count')
    plt.grid(False)
    Pearsonr=stats.pearsonr(TestY,TestPrediction)
    R2=metrics.r2_score(TestY,TestPrediction)
    RMSE=metrics.mean_squared_error(TestY,TestPrediction)**0.5
    print('Pearson correlation coefficient is {0}, and RMSE is {1}.'.format(Pearsonr[0],RMSE))
    return (Pearsonr[0],R2,RMSE)

# Save key parameters.
def WriteAccuracy(*WriteVar):
    ExcelData=openpyxl.load_workbook(WriteVar[0])
    SheetName=ExcelData.get_sheet_names()
    WriteSheet=ExcelData.get_sheet_by_name(SheetName[0])
    WriteSheet=ExcelData.active
    MaxRowNum=WriteSheet.max_row
    for i in range(len(WriteVar)-1):
        exec("WriteSheet.cell(MaxRowNum+1,i+1).value=WriteVar[i+1]")
    ExcelData.save(WriteVar[0])

# Input parameters.
DataPath="G:/CropYield/03_DL/00_Data/AllDataAll.csv"
ModelPath="G:/CropYield/03_DL/02_DNNModle"
CheckPointPath="G:/CropYield/03_DL/02_DNNModle/Weights"
CheckPointName=CheckPointPath+"/Weights_{epoch:03d}_{val_loss:.4f}.hdf5"
ParameterPath="G:/CropYield/03_DL/03_OtherResult/ParameterResult.xlsx"
TrainFrac=0.8
RandomSeed=np.random.randint(low=21,high=22)
CheckPointMethod='val_loss'
HiddenLayer=[64,128,256,512,512,1024,1024]
RegularizationFactor=0.0001
ActivationMethod='relu'
DropoutValue=[0.5,0.5,0.5,0.3,0.3,0.3,0.2]
OutputLayerActMethod='linear'
LossMethod='mean_absolute_error'
LearnRate=0.005
LearnDecay=0.0005
FitEpoch=500
BatchSize=9999
ValFrac=0.2
BestEpochOptMethod='adam'

# Fetch and divide data.
MyData=pd.read_csv(DataPath,names=['EVI0610','EVI0626','EVI0712','EVI0728','EVI0813','EVI0829',
                                   'EVI0914','EVI0930','EVI1016','Lrad06','Lrad07','Lrad08',
                                   'Lrad09','Lrad10','Prec06','Prec07','Prec08','Prec09',
                                   'Prec10','Pres06','Pres07','Pres08','Pres09','Pres10',
                                   'SIF161','SIF177','SIF193','SIF209','SIF225','SIF241',
                                   'SIF257','SIF273','SIF289','Shum06','Shum07','Shum08',
                                   'Shum09','Shum10','SoilType','Srad06','Srad07','Srad08',
                                   'Srad09','Srad10','Temp06','Temp07','Temp08','Temp09',
                                   'Temp10','Wind06','Wind07','Wind08','Wind09','Wind10',
                                   'Yield'],header=0)
TrainData=MyData.sample(frac=TrainFrac,random_state=RandomSeed)
TestData=MyData.drop(TrainData.index)

# Draw the joint distribution image.
# JointFactor=['Lrad07','Prec06','SIF161','Shum06','Srad07','Srad08','Srad10','Temp06','Yield']
# JointDistribution(JointFactor)

# Separate independent and dependent variables.
TrainX=TrainData.copy(deep=True)
TestX=TestData.copy(deep=True)
TrainY=TrainX.pop('Yield')
TestY=TestX.pop('Yield')

# Standardization data.
Normalizer=preprocessing.Normalization()
Normalizer.adapt(np.array(TrainX))

# Delete the model result from the last run.
DeleteOldModel(ModelPath)

# Find and save optimal epochs.
CallBack=CheckPoint(CheckPointName)

# Build DNN regression model.
DNNModel=BuildModel(Normalizer)
DNNModel.summary()
DNNHistory=DNNModel.fit(TrainX,
                        TrainY,
                        epochs=FitEpoch,
                        # batch_size=BatchSize,
                        verbose=1,
                        callbacks=CallBack,
                        validation_split=ValFrac)

# Draw error image.
LossPlot(DNNHistory)

# Optimize the model based on optimal epoch.
DNNModel=BestEpochIntoModel(CheckPointPath,DNNModel)

# Predict test set data.
TestPrediction=DNNModel.predict(TestX).flatten()

# Draw Test image.
TestPlot(TestY,TestPrediction)

# Verify the accuracy and draw error hist image.
AccuracyResult=AccuracyVerification(TestY,TestPrediction)
PearsonR,R2,RMSE=AccuracyResult[0],AccuracyResult[1],AccuracyResult[2]

# Save model and key parameters.
DNNModel.save(ModelPath)
WriteAccuracy(ParameterPath,PearsonR,R2,RMSE,TrainFrac,RandomSeed,CheckPointMethod,
              ','.join('%s' %i for i in HiddenLayer),RegularizationFactor,
              ActivationMethod,','.join('%s' %i for i in DropoutValue),OutputLayerActMethod,
              LossMethod,LearnRate,LearnDecay,FitEpoch,BatchSize,ValFrac,BestEpochOptMethod)

以上就是Python利用keras接口实现深度神经网络回归的详细内容，更多关于Python keras深度神经网络回归的资料请关注我们其它相关文章！