C#递归算法之归并排序

归并排序是利用递归和分而治之的技术将数据序列划分成为越来越小的半子表，再对半子表排序，最后再用递归步骤将排好序的半子表合并成为越来越大的有序序列，归并排序包括两个步骤，分别为：

1）划分子表

2）合并半子表

首先我们来讨论归并算法，归并算法将一系列数据放到一个向量中，索引范围为[first,last],这个序列由两个排好序的子表构成，以索引终点（mid）为分界线，以下面一个序列为例

7，10，19，25，12，17，21，30，48

这样的一个序列中，分为两个子序列 7,10,19,25  和 12,17,21,30,48，如下图所示：

再使用归并算法的时候的步骤如下：

第一步：比较v[indexA]=7和v[indexB]=12,将较小的v[indexA]取出来放到临时向量tempArray中，然后indexA加1

第二步：比较v[indexA]=10和v[indexB]=12,将较小的10放到临时变量tempArray中，然后indexA++;

第三步：比较v[indexA]=19与v[indexB]=12，将较小的12存放到临时变量tempArray中，然后indexB++;

第四步到第七步：按照以上规则，进行比对和存储，得到如下结果：

最后一步：将子表b中剩余项添加到临时向量tempArray中

然后将临时变量中的值按照索引位置，拷贝回向量v中，就完成了对向量v的归并排序

算法函数为：

public void Merger(int[] v, int first, int mid, int last)
{
 Queue<int> tempV = new Queue<int>();
 int indexA, indexB;
 //设置indexA，并扫描subArray1 [first,mid]
 //设置indexB,并扫描subArray2 [mid,last]
 indexA = first;
 indexB = mid;
 //在没有比较完两个子标的情况下，比较 v[indexA]和v[indexB]
 //将其中小的放到临时变量tempV中
 while (indexA < mid && indexB < last)
 {
 if (v[indexA] < v[indexB])
 {
  tempV.Enqueue(v[indexA]);
  indexA++;
 }
 else
 {
  tempV.Enqueue(v[indexB]);
  indexB++;
 }
 }
 //复制没有比较完子表中的元素
 while (indexA < mid)
 {
 tempV.Enqueue(v[indexA]);
 indexA++;
 }
 while (indexB < last)
 {
 tempV.Enqueue(v[indexB]);
 indexB++;
 }
 int index = 0;
 while (tempV.Count > 0)
 {
 v[first+index] = tempV.Dequeue();
 index++;
 }
}

实现归并排序；归并排序算法分为两步，第一步：先将原来的数据表分成排好序的子表，然后调用 Merger  对子表进行归并，使之成为有序表，例如有如下向量：

25，10，7，19，3，48，12，17，56，30，21

对此序列进行归并排序的步骤为：

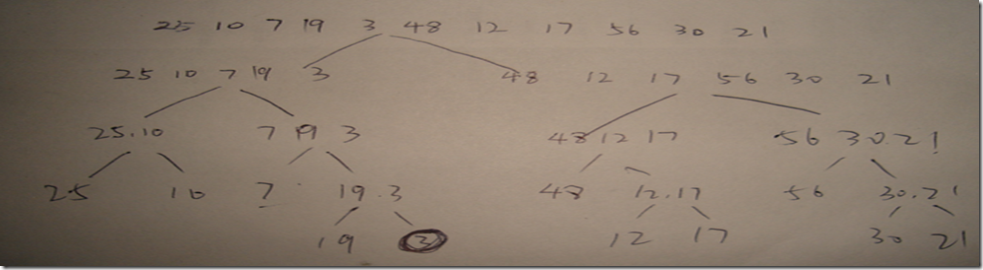
归并算法函数为

public void MergerSort(int[] v, int first, int last)
{
 if (first + 1 < last)
 {
 int mid = (first + last) / 2;
 MergerSort(v, first, mid);
 MergerSort(v, mid, last);
 Merger(v, first, mid, last);
 }
}

归并算法的划分子表和归并子表与原数据序列次序无关，因此算法的最坏情况，最坏情况和平均情况时间复杂度是一样的

下面是归并算法的函数调用图

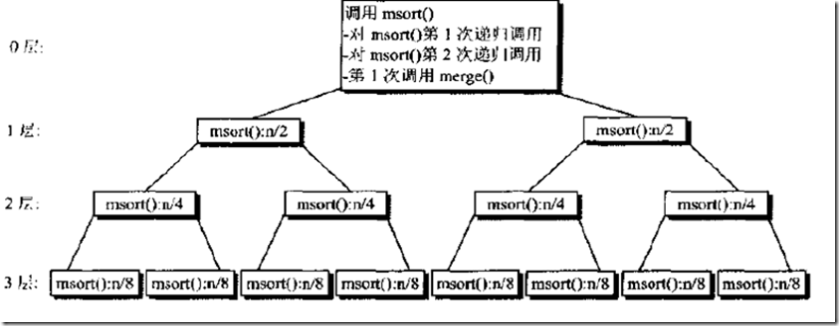
示例程序：http://xiazai.jb51.net/201606/yuanma/MergerSort(jb51.net).rar

以上就是本文的全部内容，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • C#归并排序的实现方法(递归,非递归,自然归并)

    C#归并排序的实现方法(递归,非递归,自然归并)

    //Main: 复制代码 代码如下: using System;using System.Collections.Generic;using System.Linq;using System.Text; namespace Merge{    class Program    {        static void Main(string[] args)        {            while (true)            {                Console.W

  • 归并排序的递归实现与非递归实现代码

    归并排序归并排序是建立在归并操作上的一种有效的排序算法.该算法是采用分治法(Divide and Conquer)的一个非常典型的应用.值得注意的是归并排序是一种稳定的排序方法.将已有序的子序列合并,得到完全有序的序列:即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,称为2-路归并.算法描述归并操作的工作原理如下:第一步:申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列第二步:设定两个指针,最初位置分别为两个已经排序序列的起始位置第三步:比较两个指针

  • 老生常谈比较排序之归并排序(递归)

    老生常谈比较排序之归并排序(递归)

    归并排序里运用到算法里很重要的一个思想--分治法:将原问题分解为几个规模较小但类似于原问题的子问题--<算法导论>. 在每一层递归中都有3个步骤: 1.分解问题 2.解决问题 3.合并问题的解 举例待排序数组:{6, 5, 3, 1, 7, 2, 4},将它原始序列做分解. 可以经过不断的递归分解可以看到已经把原始数组序列不断分解为最小单位,接下来不妨将它们看做是二叉树的叶子节点. 将他们进行两两归并排序形成二叉树(也称为2路归并算法),可见二叉树的根节点即为最终序列.在这个过程中我们完成了剩

  • C#递归算法之归并排序

    C#递归算法之归并排序

    归并排序是利用递归和分而治之的技术将数据序列划分成为越来越小的半子表,再对半子表排序,最后再用递归步骤将排好序的半子表合并成为越来越大的有序序列,归并排序包括两个步骤,分别为: 1)划分子表 2)合并半子表 首先我们来讨论归并算法,归并算法将一系列数据放到一个向量中,索引范围为[first,last],这个序列由两个排好序的子表构成,以索引终点(mid)为分界线,以下面一个序列为例 7,10,19,25,12,17,21,30,48 这样的一个序列中,分为两个子序列 7,10,19,25  和

  • C#递归算法之快速排序

    C#递归算法之快速排序

    上两片第归算法学习: 1)递归算法之分而治之策略 2)递归算法之归并排序 上一篇学习中介绍了了递归算法在排序中的一个应用:归并排序,在排序算法中还有一种算法用到了递归,那就是快速排序,快速排序也是一种利用了分而治之策略的算法,它由C.A.R发明,它依据中心元素的值,利用一系列递归调用将数据表划分成越来越小的子表.在每一步调用中,经过多次的交换,最终为中心元素找到最终的位置.与归并算法不同,快速排序是就地排序,而归并排序需要把元素在临时向量中拷贝,下面通过对以下向量进行排序来理解和加深快速排序算法

  • C语言非递归算法解决快速排序与归并排序产生的栈溢出

    C语言非递归算法解决快速排序与归并排序产生的栈溢出

    目录 1.栈溢出原因和递归的基本认识 2.快速排序(非递归实现) 3.归并排序(非递归实现) 建议还不理解快速排序和归并排序的小伙伴们可以先去看我上一篇博客​​​​​​哦!C语言超详细讲解排序算法下篇 1.栈溢出原因和递归的基本认识 我们先简单来了解下内存分布结构: 栈区:用于存放地址.临时变量等:                                                                            堆区:程序运行期间动态分配所使用的场景: 静态区

  • Java排序算法三之归并排序的递归与非递归的实现示例解析

    归并有递归和非递归两种. 归并的思想是: 1.将原数组首先进行两个元素为一组的排序,然后合并为四个一组,八个一组,直至合并整个数组: 2.合并两个子数组的时候,需要借助一个临时数组,用来存放当前的归并后的两个数组: 3.将临时数组复制回原数组对应的位置. 非递归的代码如下: package mergesort; import java.util.Arrays; import java.util.Random; import java.util.Scanner; //归并排序的非递归算法 publ

  • 例题详解Java dfs与记忆化搜索和分治递归算法的使用

    例题详解Java dfs与记忆化搜索和分治递归算法的使用

    目录 一.dfs(深度优先搜索) 1.图的dfs 2.树的dfs 二.记忆化搜索 1.普通递归:O(2^n) 2.记忆化搜索: O(n) 三.分治 四.算法题 1.dia和威严 示例 2.小红点点点 示例1 3.kotori和素因子 示例1 示例2 4.kotori和糖果 示例 一.dfs(深度优先搜索) 1.图的dfs /** * 深度优先搜索 * * @param node * @param set */ public void DFS(Node node, Set<Node> set)

  • Python实现希尔排序,归并排序和桶排序的示例代码

    Python实现希尔排序,归并排序和桶排序的示例代码

    目录 1. 前言 2. 希尔排序 2.1 前后切分 2.2 增量切分 3. 归并排序 3.1 分解子问题 3.2 求解子问题 3.3 合并排序 4. 基数排序 5. 总结 1. 前言 本文将介绍希尔排序.归并排序.基数排序(桶排序). 在所有的排序算法中,冒泡.插入.选择属于相类似的排序算法,这类算法的共同点:通过不停地比较,再使用交换逻辑重新确定数据的位置. 希尔.归并.快速排序算法也可归为同一类,它们的共同点都是建立在分治思想之上.把大问题分拆成小问题,解决所有小问题后,再合并每一个小问题的

  • C语言常见排序算法归并排序

    C语言常见排序算法归并排序

    目录 前言 一.归并排序 1.1 基本思想 1.2 算法思想 1.3 程序设计思想 1.4 程序实现 1.5 归并排序的特性总结 前言 本期为大家带来的是常见排序算法中的归并排序,博主在这里先分享归并排序的递归算法,包您一看就会,快来试试吧~ 一.归并排序 1.1 基本思想 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法 (Divide and Conquer)的一个非常典型的应用.将已有序的子序列合并,得到完全有序的序 列:即先使每个子序列有序,再使

  • C++递归算法实例代码

    递归算法,总结起来具有以下几个特点: 特点1  它有一个基本部分,即直接满足条件,输出     特点2  它有一个递归部分,即 通过改变基数(即n),来逐步使得n满足基本部分的条件,从而输出     特点3  在实现的过程中,它采用了分治法的思想:        即将整体分割成部分,并总是从最小的部分(基本部分)开始入手(输出),其背后的原理在于 当整体递归到部分时,会保留整体的信息,部分满足条件输出的结果会被回溯给整体使用,从而使得整体输出结果.     特点4  每一步操作,整体都会将部分当

  • C++基于递归算法解决汉诺塔问题与树的遍历功能示例

    C++基于递归算法解决汉诺塔问题与树的遍历功能示例

    本文实例讲述了C++基于递归算法解决汉诺塔问题与树的遍历功能.分享给大家供大家参考,具体如下: 递归是把问题转化为规模缩小的同类问题,然后迭代调用函数(或过程)求得问题的解.递归函数就是直接或间接调用自身的函数. 递归两要素:递归关系和递归边界(终止条件),递归关系确定了迭代的层次结构,需要深入了解并分解问题:终止条件保证了程序的有穷性. 递归的应用有很多,常见的包括:阶乘运算.斐波那契数列.汉诺塔.数的遍历,还有大名鼎鼎的快排等等.理论上,递归问题都可以由多层循环来实现.递归的每次调用都会消耗

  • JS基于递归算法实现1,2,3,4,5,6,7,8,9倒序放入数组中的方法

    JS基于递归算法实现1,2,3,4,5,6,7,8,9倒序放入数组中的方法

    本文实例讲述了JS基于递归算法实现1,2,3,4,5,6,7,8,9倒序放入数组中的方法.分享给大家供大家参考,具体如下: var array = [1, 2, 3, 4, 5, 6, 7, 8, 9]; function reverseDump(start) { start++; if (start > array.length / 2) { return; } var temp = array[start]; array[start] = array[array.length - start

随机推荐