Java数据结构BFS广搜法解决迷宫问题

目录

• 1.例题
• 题目描述
• 输入
• 输出
• 测试数据 
• 2. 思路分析
• 基本思想
• 具体步骤
• 代码实现
• 3.BFS小结
• 求解思路：
• 注意

1.例题

题目描述

迷宫由 n 行 m 列的单元格组成，每个单元格要么是空地，要么是障碍物。其中1表示空地，可以走通，2表示障碍物。给定起点坐标startx,starty以及终点坐标endx，endy。现请你找到一条从起点到终点的最短路径长度。

输入

第一行包含两个整数n,m（1<=n,m<=1000）。接下来 n 行，每行包含m个整数（值1或2），用于表示这个二维迷宫。接下来一行包含四个整数startx，starty，endx，endy，分别表示起点坐标和终点坐标。

输出

如果可以从给定的起点到终点，输出最短路径长度，否则输出NO。 

测试数据 

输入

5 4

1 1 2 1

1 1 1 1

1 1 2 1

1 2 1 1

1 1 1 2

输出

7

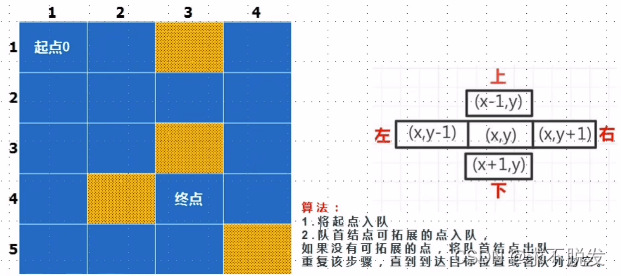
2. 思路分析

基本思想

这道题属于一道较为经典的BFS图的广度优先搜索算法例题。类似于一个分层搜索的过程，广度优先搜索需要使用一个队列以保持访问过的结点的顺序，以便按这个顺序访问这些结点的邻接结点。即从给定的起点开始向四周扩散，判断是否能够到达终点，如果不能，就继续BFS广搜，直到能够到达终点或者将所有结点遍历完一遍。在搜索前定义一个flag变量用来标记是否到达终点。

具体步骤

1）访问初始结点 p 并标记结点 p 为已访问。

2）结点 p 入队列

3）当队列非空时，继续执行，否则算法结束。

4）出队列取得队头结点 first

5）查找结点 first 的第一个方向的邻接结点 newp 。

6）若结点 first 的邻接结点 newp 不存在，则转到步骤3：否则循环执行以下三个步骤：

• 6.1若结点 newp 尚未被访问并且可以走通，则访问结点 newp 并标记为已访问。
• 6.2结点 newp 入队列
• 6.3查找结点 first 的继 newp 邻接结点后的下个邻接结点 newp ．转到步骤6

代码实现

import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	//n*m的地图，(startx,starty)起点坐标，(endx,endy)终点坐标
	static int n, m, startx, starty, endx, endy;
	static int[][] map;//地图
	static boolean[][] vistied;//标记当前点是否已经走过
	static int[][] step = { { 1, 0 }, { 0, 1 }, { -1, 0 }, { 0, -1 } };
	/*
	 * 上下左右移动遍历搜索 1 ,0 表示 x + 1 ，y + 0 向右移动，其他同理 如果为八向连通 则加上, { 1, 1 }, { 1, -1 }, {
	 * -1, 1 }, { -1, -1 } 代表斜向移动
	 */
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt();
		m = sc.nextInt();
		map = new int[n + 2][m + 2];//+2是为了防止点在边界时，四方向移动造成下标出现-1越界。
		vistied = new boolean[n + 2][m + 2];
		// 录入数据图  下标（1~n）*（1~m）
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				map[i][j] = sc.nextInt();
			}
		}
		//录入起点和终点坐标
		startx = sc.nextInt();
		starty = sc.nextInt();
		endx = sc.nextInt();
		endy = sc.nextInt();
		bfs(startx, starty);//BFS广搜
	}

	private static void bfs(int x, int y) {
		point p = new point(x, y, 0);//初始化point类封装x，y坐标以及step步数
		LinkedList<point> queue = new LinkedList<point>();//需要用到的队列
		queue.add(p);//将当前点入队列
		vistied[x][y] = true;//标记成已访问
		boolean flag = false;//是否达到终点标记
		//只要队列不为空，就说明还有路可走
		while (!queue.isEmpty()) {
			point first = queue.getFirst();//取出队列的第一个点
			if (first.x == endx && first.y == endy) {//判断当前点是否与终点坐标重合
				System.out.println(first.step);//打印需要走的步数
				flag = true;//标记已经到达终点
				break;//结束BFS
			}
			//未到达终点则进行上下左右四个方向移动
			for (int i = 0; i < 4; i++) {
				//横纵坐标变换实现位置移动
				int newx = first.x + step[i][0];
				int newy = first.y + step[i][1];
				int newstep = first.step + 1;//每一动一次步数要+1
				//判断移动后的新位置可以走，并且没走过
				if (map[newx][newy] == 1 && vistied[newx][newy] == false) {
					point newp = new point(newx, newy, newstep);//封装数据
					queue.add(newp);//入队列
					vistied[newx][newy] = true;//标记已经走过
				}
			}
			queue.removeFirst();//四个方向判断完成后，要将队首元素出列
		}
		if (!flag)//如果无法到达终点提示
			System.out.println("NO");
	}
}
//定义一个位置点的class，方便封装数据入队列
class point {
	int x;
	int y;
	int step;//从起点走到当前点需要走的步数

	public point(int x, int y, int step) {
		this.x = x;
		this.y = y;
		this.step = step;
	}
}

3.BFS小结

求解思路：

将队首结点可拓展的点入队，如果没有可拓展的点，将队首结点出队。重复以上步骤，直到到达目标位置或者队列为空。

注意

bfs先找到的一定是最短的。但是如果是加权边的话这样就会出问题了，bfs传回的是经过 边数 最少的解，但是因为加权了，这个解到根节点的 距离 不一定最短。 比如1000+1000是只有两段，1+1+1+1有4段，由于bfs返回的经过边数最少的解，这里会返回总长度2000的那个解，显然不是距离最短的路径 。BFS 运用到了队列。

到此这篇关于Java数据结构BFS广搜法解决迷宫问题的文章就介绍到这了,更多相关Java 迷宫问题内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！