C语言进阶二叉树的基础与销毁及层序遍历详解

• 单值二叉树

难度简单

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回true；否则返回false。

示例 1：

输入：[1,1,1,1,1,null,1]
输出：true

示例 2：

输入：[2,2,2,5,2]
输出：false

提示：

给定树的节点数范围是[1, 100]。

每个节点的值都是整数，范围为[0, 99]。

解1：

最简单易懂的解法，先序遍历一遍，把每个节点都和那个根节点的val值相比。最后判断flag是否为真，若为假，则表明树中有某节点的值不符。

其中的return语句是为了避免一些无意义的比较，但是其实第一个if的flag判断完全可以写在左递归之后，判断一下，如果左递归将flag置为了假，则直接return，不会进入右子树。如果按照上方解法来说，就是进入右子树之后，发现flag为假，再退出。

OJ题里的全局变量需要小心使用，若isUnivalTree里的flag不置为真，则多个测试用例时，可能会承接上一个测试用例假的结果。发生错误。

解法2：

class Solution {
public:
    bool isUnivalTree(TreeNode* root) {
        if(root == NULL)
            return true;
        if(root->left != nullptr && root->left->val != root->val)
            return false;
        if(root->right != nullptr && root->right->val != root->val)
            return false;
        return isUnivalTree(root->left)
            && isUnivalTree(root->right);
    }
};

判断每个结点和其两个子节点是否相同，当然，需要确保子节点非空，若存在不同的，直接返回false，然后递归其左右子树。

其实这个的实质就是前序遍历，对每个结点的操作就是比较它和两个子节点的值是否相同。每个结点如果都和其左右子结点相同，那么这棵树也就都相同了，如果某处不同，则返回false，层层返回，最终也会返回flase。

解法3：

class Solution {
public:
    bool isUnivalTree(TreeNode* root) {
        bool ret = PreOrder(root, root->val);
        return ret;
    }
    bool PreOrder(TreeNode* root, int val)
    {
        if(root == nullptr)
            return true;
        if(root->val != val)
            return false;
        return PreOrder(root->left, val)
            && PreOrder(root->right, val);
    }
};

与2相比没什么大的改进，只是比较的方式不同而已，仍然是前序遍历的思想。 第三个return里的&&挺好，左是假则不会对右求值。

• 相同的树

难度简单844

给你两棵二叉树的根节点p和q，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

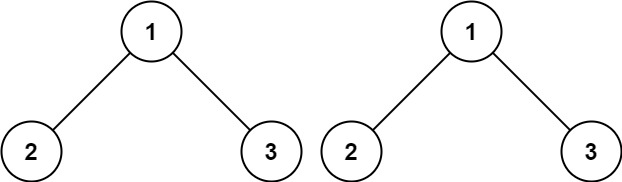
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

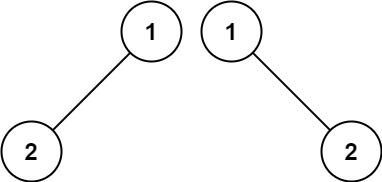
输入：p = [1,2], q = [1,null,2]
​​​​​​​输出：false

示例 3：

输入：p = [1,2,1], q = [1,1,2]
​​​​​​​输出：false

提示：

• 两棵树上的节点数目都在范围[0, 100]内
• -104<= Node.val <= 104

通过次数344,943提交次数577,105

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == nullptr && q == nullptr)
            return true;
        if(!(p!=nullptr && q!=nullptr && p->val == q->val))
            return false;
        bool retl = isSameTree(p->left,q->left);
        if(retl == false)
            return false;
        bool retr = isSameTree(p->right,q->right);
        if(retr == false)
            return false;
        return true;
/*
        return isSameTree(p->left,q->left)
            && isSameTree(p->right,q->right);
*/
    }
};

亿亿亿亿亿亿亿亿亿亿旧是前序遍历,只是两棵树同时遍历而已，判断是否相同，两个递归和最后那个注释的是效果相同的。

• 对称二叉树

难度简单1942

给你一个二叉树的根节点root， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
​​​​​​​输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
​​​​​​​输出：false

提示：

• 树中节点数目在范围[1, 1000]内
• -100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

通过次数603,527提交次数1,044,923

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return isSame(root->left, root->right);
    }
    bool isSame(TreeNode* root1, TreeNode* root2)
    {
        if(root1 == nullptr && root2 == nullptr)  // 都是空，结束递归，且符合条件
            return true;
        // 两者根节点不相等，结束，不需要进一步判断了。
        if(!(root1 != nullptr && root2 != nullptr && root1->val == root2->val))
            return false;
        // 进一步判断
        return isSame(root1->left,root2->right) && isSame(root1->right,root2->left);
    }
};

依旧是前序遍历。。。。。。。。。

• 另一棵树的子树

难度简单739

给你两棵二叉树root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在，返回true；否则，返回false。

二叉树tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。

示例 1：

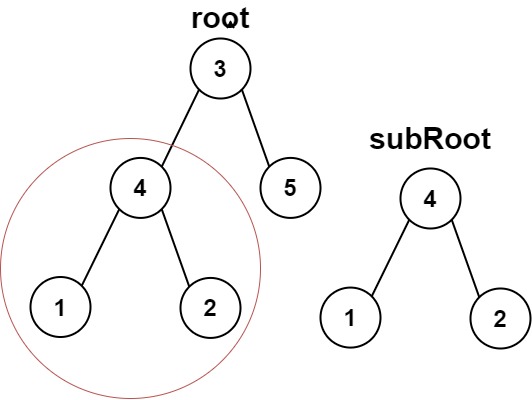
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
​​​​​​​输出：true

示例 2：

输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
​​​​​​​输出：false

提示：

• root树上的节点数量范围是[1, 2000]
• ​​​​​​​subRoot树上的节点数量范围是[1, 1000]
• ​​​​​​​-104<= root.val <= 104
• -104<= subRoot.val <= 104

通过次数125,811提交次数264,360

class Solution {
public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(root == nullptr)
            return false;
        if(isSameTree(root, subRoot);)
            return true;
        if(isSubtree(root->left,subRoot);)
            return true;
        if(isSubtree(root->right,subRoot);)
            return true;
        return false;
    }
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == nullptr && q == nullptr)
            return true;
        if(!(p!=nullptr && q!=nullptr && p->val == q->val))
            return false;
        bool retl = isSameTree(p->left,q->left);
        if(retl == false)
            return false;
        bool retr = isSameTree(p->right,q->right);
        if(retr == false)
            return false;
        return true;
    }
};

判断一个树是不是另一个的子树，这里的解法仍然是前序遍历，思路就是遍历每一个非空结点，把这个结点看成某一个树的根节点，只是这些根节点或大或小而已，然后调用isSameTree函数判断两个树是否相同。思路还是那么一个思路，没什么两样。

给出个错误解法吧：

class Solution {
public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(root == nullptr)
            return false;
        bool ret = isSameTree(root, subRoot);
        if(ret == true)
            return true;
        ret = isSameTree(root->left,subRoot);
        if(ret == true)
            return true;
        ret = isSameTree(root->right,subRoot);
        if(ret == true)
            return true;
        return false;
    }
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == nullptr && q == nullptr)
            return true;
        if(!(p!=nullptr && q!=nullptr && p->val == q->val))
            return false;
        bool retl = isSameTree(p->left,q->left);
        if(retl == false)
            return false;
        bool retr = isSameTree(p->right,q->right);
        if(retr == false)
            return false;
        return true;
    }
};

这是起初写的错误解法，仔细想想还是容易理解的，34，不同，IsSameTree函数第二个if直接返回false，不会递归，然后进入3函数的左子树调用，仍然直接返回false，再走到3的右子树，也是直接返回false。并没有起到递归的作用。

小总结：

简单来说就是遍历了一遍， 你可以直接把这个对结点的操作忽略掉，然后只看左递归和右递归，你就会发现，这两个函数恰好遍历了一遍整个树，然后你可以在适当的位置写一些操作，就是对每个结点的操作，比如572这个题，就是比较两个树是否相等。

#include<iostream>
#include<assert.h>
#include<string>
using namespace std;
typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = new BTNode();
	assert(newnode);
	newnode->data = x;
	newnode->right = nullptr;
	newnode->left = nullptr;
	return newnode;
}
BTNode* CreateTree(string s, int* pi)
{
    if(s[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    BTNode* root = BuyNode(s[(*pi)++]);
    root->left = CreateTree(s, pi);
    root->right = CreateTree(s, pi);
    return root;
}
void InOrder(BTNode* root)
{
    if(root == NULL)
        return;
    InOrder(root->left);
    cout<<root->data<<" ";
    InOrder(root->right);
}
int main()
{
    string s;
    cin >> s;
    int i = 0;
    BTNode* root = CreateTree(s, &i);
    InOrder(root);
    return 0;
}

这个题相对而言就有点新颖了，创建正确的树是关键。后面的中序遍历就是一些基本操作了。

有关根据给定字符串创建合适的二叉树：其实根本上还是一种前序遍历的思路，可以直接把这个字符串看作一个正确的二叉树，s和pi的结合可以逐个遍历每个字符，每次进入函数都会创建对应的结点。而遇到#则返回空结点，作为上一个结点的左子树或者右子树，并同时结束递归。。。。。

• 销毁二叉树

void DestroyTree(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	// 后序销毁，先销毁左子树，再销毁右子树，最后销毁根节点，对于每一棵树都是这样的操作。
	DestroyTree(root->left);
	DestroyTree(root->right);
	delete root;
}

后序销毁。。

• 层序遍历

// 层序遍历 利用队列
void LevelOrder(BTNode* root)
{
	queue<BTNode*> q;
	if (root != NULL)
	{
		q.push(root);
	}
	while (!q.empty())
	{
		BTNode* root = q.front();
		cout << root->data << " ";
		q.pop();
		if (root->left)
		{
			q.push(root->left);
		}
		if (root->right)
		{
			q.push(root->right);
		}
	}
	cout << endl;
}

利用队列，先将根节点插入队列，然后出根节点，进根节点的两个子节点，当然也有可能是一个个，也有可能只有一个根节点。 每次都是出一个结点，进这个结点的子节点。达到层序遍历的目的。

• 利用层序遍历判断一颗二叉树是否是完全二叉树

bool BinaryTreeComplete(BTNode* root)
{
	queue<BTNode*> q;
	if (root != NULL)
	{
		q.push(root);
	}
	while (!q.empty())
	{
		BTNode* root = q.front();
		q.pop();
		if (root)
		{
			q.push(root->left);
			q.push(root->right);
		}
		else
		{
			break;
		}
	}
	while (!q.empty())
	{
		if (q.front() != NULL)
			return false;
		q.pop();
	}
	return true;
}

完全二叉树的特点：层序遍历后，前方遍历的一定全是非空结点，后方一定全是空结点，利用这一特点进行判断。即：遇到空结点之后再判断队列中是否后续都是空结点。

到此这篇关于C语言进阶二叉树的基础与销毁及层序遍历详解的文章就介绍到这了,更多相关C语言二叉树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！