纯numpy数值微分法实现手写数字识别

手写数字识别作为深度学习入门经典的识别案例，各种深度学习框架都有这个例子的实现方法。我这里将不用任何深度学习现有框架，例如TensorFlow、Keras、pytorch，直接使用Python语言的numpy实现各种激活函数、损失函数、梯度下降的方法。

程序分为两部分，首先是手写数字数据的准备，直接使用如下mnist.py文件中的方法load_minist即可。文件代码如下：

# coding: utf-8
try:
    import urllib.request
except ImportError:
    raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np

url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
    'train_img':'train-images-idx3-ubyte.gz',
    'train_label':'train-labels-idx1-ubyte.gz',
    'test_img':'t10k-images-idx3-ubyte.gz',
    'test_label':'t10k-labels-idx1-ubyte.gz'
}

dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"

train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784

def _download(file_name):
    file_path = dataset_dir + "/" + file_name

    if os.path.exists(file_path):
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    print("Done")

def download_mnist():
    for v in key_file.values():
       _download(v)

def _load_label(file_name):
    file_path = dataset_dir + "/" + file_name

    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            labels = np.frombuffer(f.read(), np.uint8, offset=8)
    print("Done")

    return labels

def _load_img(file_name):
    file_path = dataset_dir + "/" + file_name

    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            data = np.frombuffer(f.read(), np.uint8, offset=16)
    data = data.reshape(-1, img_size)
    print("Done")

    return data

def _convert_numpy():
    dataset = {}
    dataset['train_img'] =  _load_img(key_file['train_img'])
    dataset['train_label'] = _load_label(key_file['train_label'])
    dataset['test_img'] = _load_img(key_file['test_img'])
    dataset['test_label'] = _load_label(key_file['test_label'])

    return dataset

def init_mnist():
    download_mnist()
    dataset = _convert_numpy()
    print("Creating pickle file ...")
    with open(save_file, 'wb') as f:
        pickle.dump(dataset, f, -1)
    print("Done!")

def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1

    return T

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集

    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label :
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组

    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):
        init_mnist()

    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)

    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0

    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])

    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 

if __name__ == '__main__':
    init_mnist()

使用上述文件中的函数就可以直接得到手写数字的训练数据、训练标签，测试样本以及测试标签。
接下里使用如下代码就可以进行手写数字的训练，代码如下：

import numpy as np
from numpy.lib.function_base import select
from dataset.mnist import load_mnist
import matplotlib.pylab as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))  

def sigmoid_grad(x):
    return (1.0 - sigmoid(x)) * sigmoid(x)

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)

        x[idx] = tmp_val # 还原值
        it.iternext()   

    return grad

#(x_train,t_train),(x_test,t_test)=load_mnist(normalize=True,one_hot_label=True)
#两层神经网络的类
class TwoLayerNet:
    def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
        #初始化权重
        self.params={}
        self.params['W1']=weight_init_std*np.random.randn(input_size,hidden_size)
        self.params['b1']=np.zeros(hidden_size)
        self.params['W2']=weight_init_std*np.random.randn(hidden_size,output_size)
        self.params['b2']=np.zeros(output_size)

    def predict(self,x):
        W1,W2=self.params['W1'],self.params['W2']
        b1,b2=self.params['b1'],self.params['b2']

        a1=np.dot(x,W1)+b1
        z1=sigmoid(a1)
        a2=np.dot(z1,W2)+b2
        y=softmax(a2)

        return y
    #损失函数
    def loss(self,x,t):
        y=self.predict(x)
        return cross_entropy_error(y,t)
    #数值微分法
    def numerical_gradient(self,x,t):
        loss_W=lambda W:self.loss(x,t)
        grads={}
        grads['W1']=numerical_gradient(loss_W,self.params['W1'])
        grads['b1']=numerical_gradient(loss_W,self.params['b1'])
        grads['W2']=numerical_gradient(loss_W,self.params['W2'])
        grads['b2']=numerical_gradient(loss_W,self.params['b2'])
        return grads

    #误差反向传播法
    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}

        batch_num = x.shape[0]

        # forward
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        # backward
        dy = (y - t) / batch_num
        grads['W2'] = np.dot(z1.T, dy)
        grads['b2'] = np.sum(dy, axis=0)

        da1 = np.dot(dy, W2.T)
        dz1 = sigmoid_grad(a1) * da1
        grads['W1'] = np.dot(x.T, dz1)
        grads['b1'] = np.sum(dz1, axis=0)

        return grads
    #准确率
    def accuracy(self,x,t):
        y=self.predict(x)
        y=np.argmax(y,axis=1)
        t=np.argmax(t,axis=1)

        accuracy=np.sum(y==t)/float(x.shape[0])
        return accuracy

if __name__=='__main__':
    (x_train,t_train),(x_test,t_test)=load_mnist(normalize=True,one_hot_label=True)
    net=TwoLayerNet(input_size=784,hidden_size=50,output_size=10)

    train_loss_list=[]

    #超参数
    iter_nums=10000
    train_size=x_train.shape[0]
    batch_size=100
    learning_rate=0.1

    #记录准确率
    train_acc_list=[]
    test_acc_list=[]
    #平均每个epoch的重复次数
    iter_per_epoch=max(train_size/batch_size,1)

    for i in range(iter_nums):
        #小批量数据
        batch_mask=np.random.choice(train_size,batch_size)
        x_batch=x_train[batch_mask]
        t_batch=t_train[batch_mask]

        #计算梯度
        #数值微分 计算很慢
        #grad=net.numerical_gradient(x_batch,t_batch)
        #误差反向传播法 计算很快
        grad=net.gradient(x_batch,t_batch)

        #更新参数 权重W和偏重b
        for key in ['W1','b1','W2','b2']:
            net.params[key]-=learning_rate*grad[key]

        #记录学习过程
        loss=net.loss(x_batch,t_batch)
        print('训练次数:'+str(i)+'    loss:'+str(loss))
        train_loss_list.append(loss)

        #计算每个epoch的识别精度
        if i%iter_per_epoch==0:
            #测试在所有训练数据和测试数据上的准确率
            train_acc=net.accuracy(x_train,t_train)
            test_acc=net.accuracy(x_test,t_test)
            train_acc_list.append(train_acc)
            test_acc_list.append(test_acc)
            print('train acc:'+str(train_acc)+'   test acc:'+str(test_acc))

    print(train_acc_list)
    print(test_acc_list)

    # 绘制图形
    markers = {'train': 'o', 'test': 's'}
    x = np.arange(len(train_acc_list))
    plt.plot(x, train_acc_list, label='train acc')
    plt.plot(x, test_acc_list, label='test acc', linestyle='--')
    plt.xlabel("epochs")
    plt.ylabel("accuracy")
    plt.ylim(0, 1.0)
    plt.legend(loc='lower right')
    plt.show()

训练完成后，查看绘制准确率的图片，可以获取到成功实现了手写数字识别。

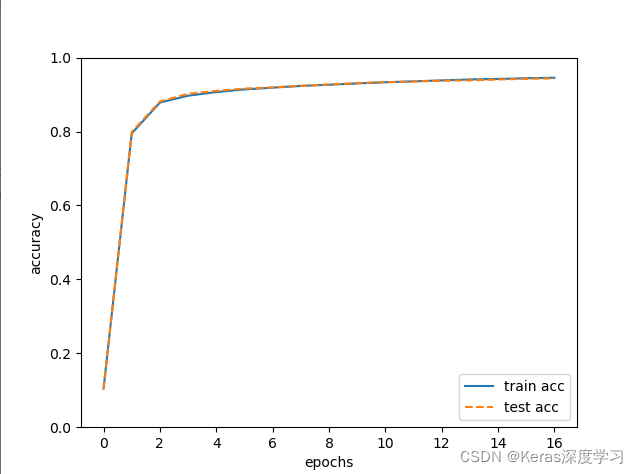
随着训练批次的增加，准确率逐渐增大接近于1，说明训练过程按着正确拟合的方向前进。

到此这篇关于纯numpy实现数值微分法实现手写数字识别的文章就介绍到这了,更多相关numpy 手写数字识别内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！