JDK集合源码之解析TreeMap(一)
目录
- 简介
- 继承体系
- 存储结构
- 源码解析
- 属性
- Entry内部类
- 构造方法
- get(Object key)方法
- 特性再回顾
- 左旋
- 右旋
- 插入元素
- 插入再平衡
- 插入元素举例
- 总结
简介
TreeMap使用红黑树存储元素,可以保证元素按key值的大小进行遍历。
继承体系

TreeMap实现了Map、SortedMap、NavigableMap、Cloneable、Serializable等接口。
SortedMap规定了元素可以按key的大小来遍历,它定义了一些返回部分map的方法。
public interface SortedMap<K,V> extends Map<K,V> {
// key的比较器
Comparator<? super K> comparator();
// 返回fromKey(包含)到toKey(不包含)之间的元素组成的子map
SortedMap<K,V> subMap(K fromKey, K toKey);
// 返回小于toKey(不包含)的子map
SortedMap<K,V> headMap(K toKey);
// 返回大于等于fromKey(包含)的子map
SortedMap<K,V> tailMap(K fromKey);
// 返回最小的key
K firstKey();
// 返回最大的key
K lastKey();
// 返回key集合
Set<K> keySet();
// 返回value集合
Collection<V> values();
// 返回节点集合
Set<Map.Entry<K, V>> entrySet();
}
NavigableMap是对SortedMap的增强,定义了一些返回离目标key最近的元素的方法。
public interface NavigableMap<K,V> extends SortedMap<K,V> {
// 小于给定key的最大节点
Map.Entry<K,V> lowerEntry(K key);
// 小于给定key的最大key
K lowerKey(K key);
// 小于等于给定key的最大节点
Map.Entry<K,V> floorEntry(K key);
// 小于等于给定key的最大key
K floorKey(K key);
// 大于等于给定key的最小节点
Map.Entry<K,V> ceilingEntry(K key);
// 大于等于给定key的最小key
K ceilingKey(K key);
// 大于给定key的最小节点
Map.Entry<K,V> higherEntry(K key);
// 大于给定key的最小key
K higherKey(K key);
// 最小的节点
Map.Entry<K,V> firstEntry();
// 最大的节点
Map.Entry<K,V> lastEntry();
// 弹出最小的节点
Map.Entry<K,V> pollFirstEntry();
// 弹出最大的节点
Map.Entry<K,V> pollLastEntry();
// 返回倒序的map
NavigableMap<K,V> descendingMap();
// 返回有序的key集合
NavigableSet<K> navigableKeySet();
// 返回倒序的key集合
NavigableSet<K> descendingKeySet();
// 返回从fromKey到toKey的子map,是否包含起止元素可以自己决定
NavigableMap<K,V> subMap(K fromKey, boolean fromInclusive,
K toKey, boolean toInclusive);
// 返回小于toKey的子map,是否包含toKey自己决定
NavigableMap<K,V> headMap(K toKey, boolean inclusive);
// 返回大于fromKey的子map,是否包含fromKey自己决定
NavigableMap<K,V> tailMap(K fromKey, boolean inclusive);
// 等价于subMap(fromKey, true, toKey, false)
SortedMap<K,V> subMap(K fromKey, K toKey);
// 等价于headMap(toKey, false)
SortedMap<K,V> headMap(K toKey);
// 等价于tailMap(fromKey, true)
SortedMap<K,V> tailMap(K fromKey);
}
存储结构
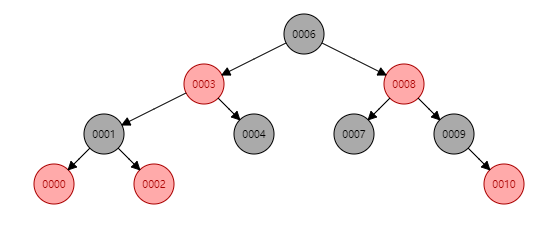
TreeMap只使用到了红黑树,所以它的时间复杂度为O(log n),我们再来回顾一下红黑树的特性。
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。(注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!)
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
源码解析
属性
/** * 比较器,如果没传则key要实现Comparable接口 */ private final Comparator<? super K> comparator; /** * 根节点 */ private transient Entry<K,V> root; /** * 元素个数 */ private transient int size = 0; /** * 修改次数 */ private transient int modCount = 0;
(1)comparator
按key的大小排序有两种方式,一种是key实现Comparable接口,一种方式通过构造方法传入比较器。
(2)root
根节点,TreeMap没有桶的概念,所有的元素都存储在一颗树中。
Entry内部类
存储节点,典型的红黑树结构。
static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
Entry<K,V> left;
Entry<K,V> right;
Entry<K,V> parent;
boolean color = BLACK;
}
构造方法
/**
* 默认构造方法,key必须实现Comparable接口
*/
public TreeMap() {
comparator = null;
}
/**
* 使用传入的comparator比较两个key的大小
*/
public TreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
}
/**
* key必须实现Comparable接口,把传入map中的所有元素保存到新的TreeMap中
*/
public TreeMap(Map<? extends K, ? extends V> m) {
comparator = null;
putAll(m);
}
/**
* 使用传入map的比较器,并把传入map中的所有元素保存到新的TreeMap中
*/
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
构造方法主要分成两类,一类是使用comparator比较器,一类是key必须实现Comparable接口。
其实,笔者认为这两种比较方式可以合并成一种,当没有传comparator的时候,可以用以下方式来给comparator赋值,这样后续所有的比较操作都可以使用一样的逻辑处理了,而不用每次都检查comparator为空的时候又用Comparable来实现一遍逻辑。
// 如果comparator为空,则key必须实现Comparable接口,所以这里肯定可以强转 // 这样在构造方法中统一替换掉,后续的逻辑就都一致了 comparator = (k1, k2) -> ((Comparable<? super K>)k1).compareTo(k2);
get(Object key)方法
获取元素,典型的二叉查找树的查找方法。
public V get(Object key) {
// 根据key查找元素
Entry<K,V> p = getEntry(key);
// 找到了返回value值,没找到返回null
return (p==null ? null : p.value);
}
final Entry<K,V> getEntry(Object key) {
// 如果comparator不为空,使用comparator的版本获取元素
if (comparator != null)
return getEntryUsingComparator(key);
// 如果key为空返回空指针异常
if (key == null)
throw new NullPointerException();
// 将key强转为Comparable
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
// 从根元素开始遍历
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
// 如果小于0从左子树查找
p = p.left;
else if (cmp > 0)
// 如果大于0从右子树查找
p = p.right;
else
// 如果相等说明找到了直接返回
return p;
}
// 没找到返回null
return null;
}
final Entry<K,V> getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator<? super K> cpr = comparator;
if (cpr != null) {
// 从根元素开始遍历
Entry<K,V> p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
// 如果小于0从左子树查找
p = p.left;
else if (cmp > 0)
// 如果大于0从右子树查找
p = p.right;
else
// 如果相等说明找到了直接返回
return p;
}
}
// 没找到返回null
return null;
}
(1)从root遍历整个树;
(2)如果待查找的key比当前遍历的key小,则在其左子树中查找;
(3)如果待查找的key比当前遍历的key大,则在其右子树中查找;
(4)如果待查找的key与当前遍历的key相等,则找到了该元素,直接返回;
(5)从这里可以看出是否有comparator分化成了两个方法,但是内部逻辑一模一样,因此可见笔者comparator = (k1, k2) -> ((Comparable<? super K>)k1).compareTo(k2);这种改造的必要性。
特性再回顾
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。(注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!)
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
左旋
左旋,就是以某个节点为支点向左旋转。
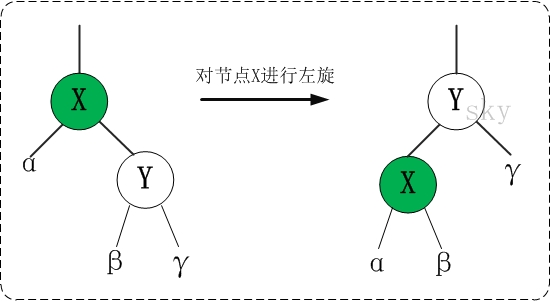
整个左旋过程如下:
(1)将 y的左节点 设为 x的右节点,即将 β 设为 x的右节点;
(2)将 x 设为 y的左节点的父节点,即将 β的父节点 设为 x;
(3)将 x的父节点 设为 y的父节点;
(4)如果 x的父节点 为空节点,则将y设置为根节点;如果x是它父节点的左(右)节点,则将y设置为x父节点的左(右)节点;
(5)将 x 设为 y的左节点;
(6)将 x的父节点 设为 y;
让我们来看看TreeMap中的实现:
/**
* 以p为支点进行左旋
* 假设p为图中的x
*/
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
// p的右节点,即y
Entry<K,V> r = p.right;
// (1)将 y的左节点 设为 x的右节点
p.right = r.left;
// (2)将 x 设为 y的左节点的父节点(如果y的左节点存在的话)
if (r.left != null)
r.left.parent = p;
// (3)将 x的父节点 设为 y的父节点
r.parent = p.parent;
// (4)...
if (p.parent == null)
// 如果 x的父节点 为空,则将y设置为根节点
root = r;
else if (p.parent.left == p)
// 如果x是它父节点的左节点,则将y设置为x父节点的左节点
p.parent.left = r;
else
// 如果x是它父节点的右节点,则将y设置为x父节点的右节点
p.parent.right = r;
// (5)将 x 设为 y的左节点
r.left = p;
// (6)将 x的父节点 设为 y
p.parent = r;
}
}
右旋
右旋,就是以某个节点为支点向右旋转。
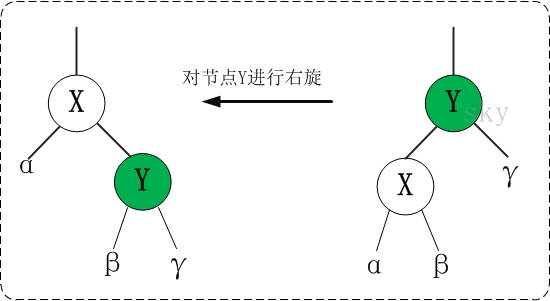
整个右旋过程如下:
(1)将 x的右节点 设为 y的左节点,即 将 β 设为 y的左节点;
(2)将 y 设为 x的右节点的父节点,即 将 β的父节点 设为 y;
(3)将 y的父节点 设为 x的父节点;
(4)如果 y的父节点 是 空节点,则将x设为根节点;如果y是它父节点的左(右)节点,则将x设为y的父节点的左(右)节点;
(5)将 y 设为 x的右节点;
(6)将 y的父节点 设为 x;
让我们来看看TreeMap中的实现:
/**
* 以p为支点进行右旋
* 假设p为图中的y
*/
private void rotateRight(Entry<K,V> p) {
if (p != null) {
// p的左节点,即x
Entry<K,V> l = p.left;
// (1)将 x的右节点 设为 y的左节点
p.left = l.right;
// (2)将 y 设为 x的右节点的父节点(如果x有右节点的话)
if (l.right != null) l.right.parent = p;
// (3)将 y的父节点 设为 x的父节点
l.parent = p.parent;
// (4)...
if (p.parent == null)
// 如果 y的父节点 是 空节点,则将x设为根节点
root = l;
else if (p.parent.right == p)
// 如果y是它父节点的右节点,则将x设为y的父节点的右节点
p.parent.right = l;
else
// 如果y是它父节点的左节点,则将x设为y的父节点的左节点
p.parent.left = l;
// (5)将 y 设为 x的右节点
l.right = p;
// (6)将 y的父节点 设为 x
p.parent = l;
}
}
插入元素
插入元素,如果元素在树中存在,则替换value;如果元素不存在,则插入到对应的位置,再平衡树。
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
// 如果没有根节点,直接插入到根节点
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
// key比较的结果
int cmp;
// 用来寻找待插入节点的父节点
Entry<K,V> parent;
// 根据是否有comparator使用不同的分支
Comparator<? super K> cpr = comparator;
if (cpr != null) {
// 如果使用的是comparator方式,key值可以为null,只要在comparator.compare()中允许即可
// 从根节点开始遍历寻找
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
// 如果小于0从左子树寻找
t = t.left;
else if (cmp > 0)
// 如果大于0从右子树寻找
t = t.right;
else
// 如果等于0,说明插入的节点已经存在了,直接更换其value值并返回旧值
return t.setValue(value);
} while (t != null);
}
else {
// 如果使用的是Comparable方式,key不能为null
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
// 从根节点开始遍历寻找
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
// 如果小于0从左子树寻找
t = t.left;
else if (cmp > 0)
// 如果大于0从右子树寻找
t = t.right;
else
// 如果等于0,说明插入的节点已经存在了,直接更换其value值并返回旧值
return t.setValue(value);
} while (t != null);
}
// 如果没找到,那么新建一个节点,并插入到树中
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
// 如果小于0插入到左子节点
parent.left = e;
else
// 如果大于0插入到右子节点
parent.right = e;
// 插入之后的平衡
fixAfterInsertion(e);
// 元素个数加1(不需要扩容)
size++;
// 修改次数加1
modCount++;
// 如果插入了新节点返回空
return null;
}
插入再平衡
插入的元素默认都是红色,因为插入红色元素只违背了第4条特性,那么我们只要根据这个特性来平衡就容易多了。
根据不同的情况有以下几种处理方式:
- 插入的元素如果是根节点,则直接涂成黑色即可,不用平衡;
- 插入的元素的父节点如果为黑色,不需要平衡;
- 插入的元素的父节点如果为红色,则违背了特性4,需要平衡,平衡时又分成下面三种情况:
(如果父节点是祖父节点的左节点)
| 情况 | 策略 |
|---|---|
| 1)父节点为红色,叔叔节点也为红色 | (1)将父节点设为黑色; (2)将叔叔节点设为黑色; (3)将祖父节点设为红色; (4)将祖父节点设为新的当前节点,进入下一次循环判断; |
| 2)父节点为红色,叔叔节点为黑色,且当前节点是其父节点的右节点 | (1)将父节点作为新的当前节点; (2)以新当节点为支点进行左旋,进入情况3); |
| 3)父节点为红色,叔叔节点为黑色,且当前节点是其父节点的左节点 | (1)将父节点设为黑色; (2)将祖父节点设为红色; (3)以祖父节点为支点进行右旋,进入下一次循环判断; |
(如果父节点是祖父节点的右节点,则正好与上面反过来)
| 情况 | 策略 |
|---|---|
| 1)父节点为红色,叔叔节点也为红色 | (1)将父节点设为黑色; (2)将叔叔节点设为黑色; (3)将祖父节点设为红色; (4)将祖父节点设为新的当前节点,进入下一次循环判断; |
| 2)父节点为红色,叔叔节点为黑色,且当前节点是其父节点的左节点 | (1)将父节点作为新的当前节点; (2)以新当节点为支点进行右旋; |
| 3)父节点为红色,叔叔节点为黑色,且当前节点是其父节点的右节点 | (1)将父节点设为黑色; (2)将祖父节点设为红色; (3)以祖父节点为支点进行左旋,进入下一次循环判断; |
让我们来看看TreeMap中的实现:
/**
* 插入再平衡
*(1)每个节点或者是黑色,或者是红色。
*(2)根节点是黑色。
*(3)每个叶子节点(NIL)是黑色。(注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!)
*(4)如果一个节点是红色的,则它的子节点必须是黑色的。
*(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
*/
private void fixAfterInsertion(Entry<K,V> x) {
// 插入的节点为红节点,x为当前节点
x.color = RED;
// 只有当插入节点不是根节点且其父节点为红色时才需要平衡(违背了特性4)
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// a)如果父节点是祖父节点的左节点
// y为叔叔节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
// 情况1)如果叔叔节点为红色
// (1)将父节点设为黑色
setColor(parentOf(x), BLACK);
// (2)将叔叔节点设为黑色
setColor(y, BLACK);
// (3)将祖父节点设为红色
setColor(parentOf(parentOf(x)), RED);
// (4)将祖父节点设为新的当前节点
x = parentOf(parentOf(x));
} else {
// 如果叔叔节点为黑色
// 情况2)如果当前节点为其父节点的右节点
if (x == rightOf(parentOf(x))) {
// (1)将父节点设为当前节点
x = parentOf(x);
// (2)以新当前节点左旋
rotateLeft(x);
}
// 情况3)如果当前节点为其父节点的左节点(如果是情况2)则左旋之后新当前节点正好为其父节点的左节点了)
// (1)将父节点设为黑色
setColor(parentOf(x), BLACK);
// (2)将祖父节点设为红色
setColor(parentOf(parentOf(x)), RED);
// (3)以祖父节点为支点进行右旋
rotateRight(parentOf(parentOf(x)));
}
} else {
// b)如果父节点是祖父节点的右节点
// y是叔叔节点
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
// 情况1)如果叔叔节点为红色
// (1)将父节点设为黑色
setColor(parentOf(x), BLACK);
// (2)将叔叔节点设为黑色
setColor(y, BLACK);
// (3)将祖父节点设为红色
setColor(parentOf(parentOf(x)), RED);
// (4)将祖父节点设为新的当前节点
x = parentOf(parentOf(x));
} else {
// 如果叔叔节点为黑色
// 情况2)如果当前节点为其父节点的左节点
if (x == leftOf(parentOf(x))) {
// (1)将父节点设为当前节点
x = parentOf(x);
// (2)以新当前节点右旋
rotateRight(x);
}
// 情况3)如果当前节点为其父节点的右节点(如果是情况2)则右旋之后新当前节点正好为其父节点的右节点了)
// (1)将父节点设为黑色
setColor(parentOf(x), BLACK);
// (2)将祖父节点设为红色
setColor(parentOf(parentOf(x)), RED);
// (3)以祖父节点为支点进行左旋
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 平衡完成后将根节点设为黑色
root.color = BLACK;
}
插入元素举例
我们依次向红黑树中插入 4、2、3 三个元素,来一起看看整个红黑树平衡的过程。
三个元素都插入完成后,符合父节点是祖父节点的左节点,叔叔节点为黑色,且当前节点是其父节点的右节点,即情况2)。

情况2)需要做以下两步处理:
(1)将父节点作为新的当前节点;
(2)以新当节点为支点进行左旋,进入情况3);
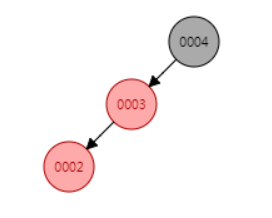
情况3)需要做以下三步处理:
(1)将父节点设为黑色;
(2)将祖父节点设为红色;
(3)以祖父节点为支点进行右旋,进入下一次循环判断;
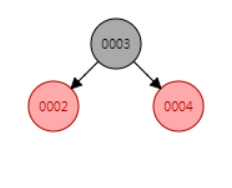
下一次循环不符合父节点为红色了,退出循环,插入再平衡完成。
总结
本篇文章就到这里了,希望能给你带来帮助,也希望您能够多多关注我们的更多内容!

