Python地图四色原理的遗传算法着色实现

目录

• 1 任务需求
• 2 代码实现
• 2.1 基本思路
• 2.3 结果展示
• 总结

1 任务需求

  首先，我们来明确一下本文所需实现的需求。

  现有一个由多个小图斑组成的矢量图层，如下图所示；我们需要找到一种由4种颜色组成的配色方案，对该矢量图层各图斑进行着色，使得各相邻小图斑间的颜色不一致，如下下图所示。

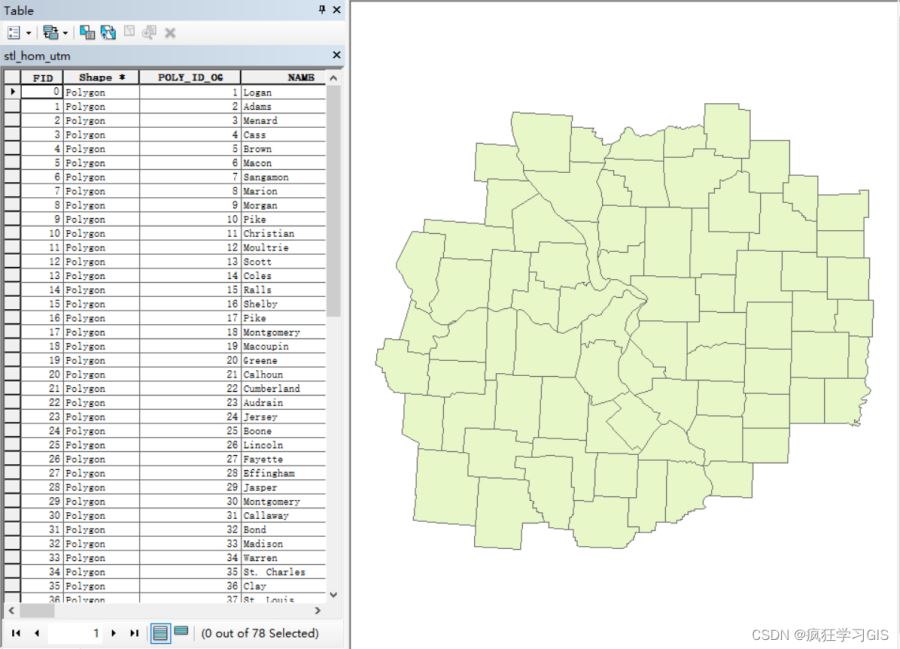
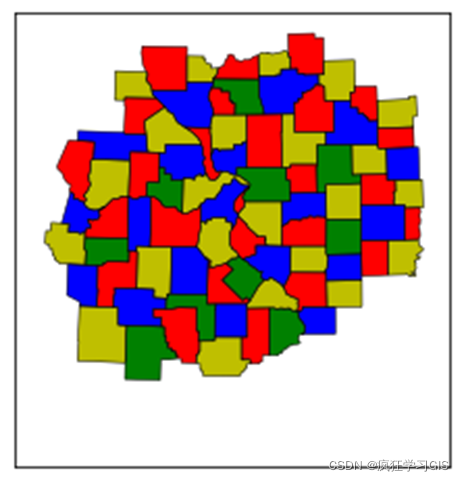
  在这里，我们用到了四色定理（Four Color Theorem），又称四色地图定理（Four Color Map Theorem）：如果在平面上存在一些邻接的有限区域，则至多仅用四种颜色来给这些不同的区域染色，就可以使得每两个邻接区域染的颜色都不一样。

2 代码实现

  明确了需求，我们就可以开始具体的代码编写。目前国内各大博客中，有很多关于Python实现地图四色原理着色的代码，其中大多数是基于回溯法来实现的；而在一个英文博客网页中，看到了基于遗传算法的地图四色原理着色实现。那么就以该代码为例，进行操作。在这里，由于我本人对于遗传算法的理解还并不深入，因此在代码介绍方面或多或少还存在着一定不足，希望大家多多批评指正。

2.1 基本思路

  遗传算法是一种用于解决最佳化问题的搜索算法，属于进化算法范畴。结合前述需求，首先可以将每一个区域的颜色作为一个基因，个体基因型则为全部地区（前述矢量图层共有78个小图斑，即78个区域）颜色基因的汇总；通过构建Rule类，将空间意义上的“相邻”转换为可以被遗传算法识别（即可以对个体基因改变加以约束）的信息；随后，结合子代的更替，找到满足要求的基因组；最终将得到的基因组再转换为空间意义上的颜色信息，并输出结果。

  具体分步骤思路如下：

定义“规则”。“规则”用以将区域之间的空间连接情况转换为遗传算法可以识别的信息；被“规则”连接的两个区域在空间中是相邻的。定义区域空间连接情况检查所需函数。这些函数用于检查两两区域之间的连接性是否满足逻辑；例如，若在“规则”中显示区域A与区域B连接，那么区域B也必须在“规则”中显示与区域A连接。定义个体基因型。其中，各个体具有78个基因，每一个基因表示一个区域的颜色。个体更替与最优基因选择。通过个体的不断更迭，选择出满足“规则”要求的个体基因型。基因型解释。将得到的个体基因型进行解释，相当于第一步的反过程，即将基因信息转换为空间连接情况。结果检查。检查所得到的颜色与最优个体基因组中的各个基因是否一致。 2.2 代码讲解

  接下来，将完整代码进行介绍。其中，shapefile_path即为矢量图层的保存路径；"POLY_ID_OG"则为矢量图层的属性表中的一个字段，其代表每一个小图斑的编号。

# -*- coding: utf-8 -*-
"""
Created on Sun Oct 31 19:22:33 2021

@author: Chutj
"""

import genetic
import unittest
import datetime
from libpysal.weights import Queen

shapefile_path="G:/Python_Home1/stl_hom_utm.shp"

weights=Queen.from_shapefile(shapefile_path,"POLY_ID_OG")
one_neighbor_other=weights.neighbors

# 定义“规则”，用以将区域之间的空间连接情况转换为遗传算法可以识别的信息。被“规则”连接的两个区域在空间中是相邻的

class Rule:
    Item = None
    Other = None
    Stringified = None

    def __init__(self, item, other, stringified):
        self.Item = item
        self.Other = other
        self.Stringified = stringified

    def __eq__(self, another):
        return hasattr(another, 'Item') and \
               hasattr(another, 'Other') and \
               self.Item == another.Item and \
               self.Other == another.Other

    def __hash__(self):
        return hash(self.Item) * 397 ^ hash(self.Other)

    def __str__(self):
        return self.Stringified

# 定义区域空间连接情况检查所需函数，用以确保区域两两之间相邻情况的准确

def buildLookup(items):
    itemToIndex = {}
    index = 0
    for key in sorted(items):
        itemToIndex[key] = index
        index += 1
    return itemToIndex

def buildRules(items):
    itemToIndex = buildLookup(items.keys())
    rulesAdded = {}
    rules = []
    keys = sorted(list(items.keys()))

    for key in sorted(items.keys()):
        keyIndex = itemToIndex[key]
        adjacentKeys = items[key]
        for adjacentKey in adjacentKeys:
            if adjacentKey == '':
                continue
            adjacentIndex = itemToIndex[adjacentKey]
            temp = keyIndex
            if adjacentIndex < temp:
                temp, adjacentIndex = adjacentIndex, temp
            ruleKey = str(keys[temp]) + "->" + str(keys[adjacentIndex])
            rule = Rule(temp, adjacentIndex, ruleKey)
            if rule in rulesAdded:
                rulesAdded[rule] += 1
            else:
                rulesAdded[rule] = 1
                rules.append(rule)

    for k, v in rulesAdded.items():
        if v == 1:
            print("rule %s is not bidirectional" % k)

    return rules

# 定义颜色所代表的基因组

colors = ["Orange", "Yellow", "Green", "Blue"]
colorLookup = {}
for color in colors:
    colorLookup[color[0]] = color
geneset = list(colorLookup.keys())

# 定义个体基因型，其中各个体有78个基因，每一个基因代表一个区域。个体基因需要满足“规则”中相邻的区域具有不同的颜色

class GraphColoringTests(unittest.TestCase):
    def test(self):
        rules = buildRules(one_neighbor_other)
        colors = ["Orange", "Yellow", "Green", "Blue"]
        colorLookup = {}
        for color in colors:
            colorLookup[color[0]] = color
        geneset = list(colorLookup.keys())
        optimalValue = len(rules)
        startTime = datetime.datetime.now()
        fnDisplay = lambda candidate: display(candidate, startTime)
        fnGetFitness = lambda candidate: getFitness(candidate, rules)
        best = genetic.getBest(fnGetFitness, fnDisplay, len(one_neighbor_other), optimalValue, geneset)
        self.assertEqual(best.Fitness, optimalValue)

        keys = sorted(one_neighbor_other.keys())

        for index in range(len(one_neighbor_other)):
            print(keys[index]," is ",colorLookup[best.Genes[index]])

# 输出各区域颜色

def display(candidate, startTime):
    timeDiff = datetime.datetime.now() - startTime
    print("%s\t%i\t%s" % (''.join(map(str, candidate.Genes)), candidate.Fitness, str(timeDiff)))

# 检查各区域颜色是否与个体基因所代表的颜色一致

def getFitness(candidate, rules):
    rulesThatPass = 0
    for rule in rules:
        if candidate[rule.Item] != candidate[rule.Other]:
            rulesThatPass += 1

    return rulesThatPass

# 运行程序

GraphColoringTests().test()

2.3 结果展示

  执行上述代码，即可得到结果。在这里值得一提的是：这个代码不知道是其自身原因，还是我电脑的问题，执行起来非常慢——单次运行时间可能在5 ~ 6个小时左右，实在太慢了；大家如果感兴趣，可以尝试着能不能将代码的效率提升一下。

  代码执行完毕后得到的结果是文字形式的，具体如下图所示。

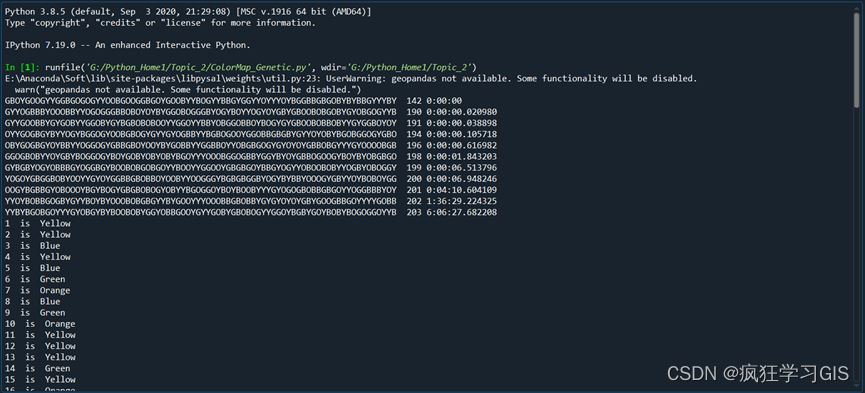
  可以看到，通过203次迭代，找到了满足要求的地图配色方案，用时06小时06分钟；代码执行结果除显示出具体个体的整体基因型之外，还将分别显示78个小区域（小图斑）各自的具体颜色名称（我上面那幅图没有截全，实际上是78个小区域的颜色都会输出的）。

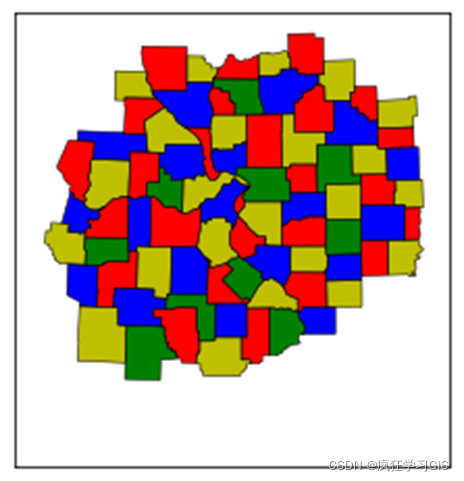
  当然，大家也可以发现，这种文字表达的代码执行结果显然不如直接来一幅如下所示的结果图直观。但是，由于代码单次执行时间实在是太久了，我也没再腾出时间（其实是偷懒）对结果的可视化加以修改。大家如果感兴趣的话，可以尝试对代码最终的结果呈现部分加以修改——例如，可以通过Matplotlib库的拓展——Basemap库将78个小区域的配色方案进行可视化。

总结

到此这篇关于Python地图四色原理的遗传算法着色实现的文章就介绍到这了,更多相关Python地图四色原理内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！