Java源码解析之平衡二叉树

一、平衡二叉树的定义

平衡二叉树是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1 。它是一种高度平衡的二叉排序树。意思是说，要么它是一棵空树，要么它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1 。我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF (Balance Factor)，那么平衡二叉树上所有结点的平衡因子只可能是-1 、0 和1。

这里举个栗子：

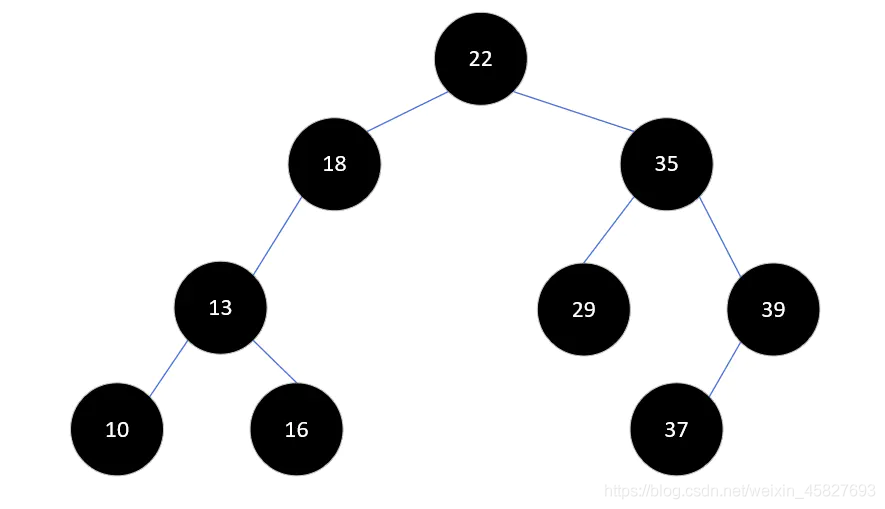
仔细看图中值为18的节点，18的节点的深度为2 。而它的右子树的深度为0，其差值的绝对值大于1了，所以这不是一科平衡二叉树。

二、平衡二叉树的实现原理

平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个节点时，先检查是否因插入而破坏了树的平衡性，如果是，则找出最小不平衡二叉树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各节点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。最小不平衡子树是指距离插入节点最近，且平衡因子的绝对值大于1的节点为根的子树。

下面就让我们通过一个栗子来看看平衡二叉树是怎么构建的呢

首先我们将{3, 2, 1, 4, 5, 6, 7, 10, 9, 8}这样的数组构建成一个二叉排序树，按照二叉排序树的性质，我们将得到下图这样的树：

从图中可以看出，树的高度达到了8，对于查找和插入效率肯定是不够理想的。
接下里我们来看看怎么将这颗二叉排序树一步步构建成平衡二叉树的：

1.按数组顺序将2和3插入，此时没有什么影响，3的平衡因子为1， 2的平衡因子为0，到这里还没什么问题

2.此时我们再来插入1，根据二叉排序树，1只能是2的左子树，然而此时3的平衡因子为2，已经不符合平衡二叉树的规则，这个时候，这棵树就是最小不平衡子树

3.我们将其右旋：三个元素的平衡因子都为0，没什么毛病，我们继续

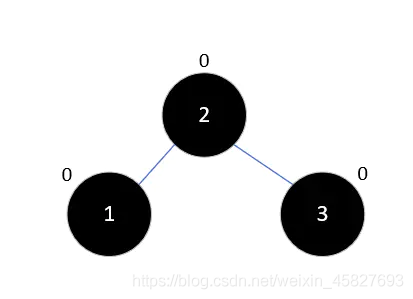
4.在插入4，根据二叉排序树的规则，4只能放在3的右子树，此时没什么大毛病，我们继续

5.在插入元素5，同理，5只能放在4的右子树，此时元素2的平衡因子为2大于1，

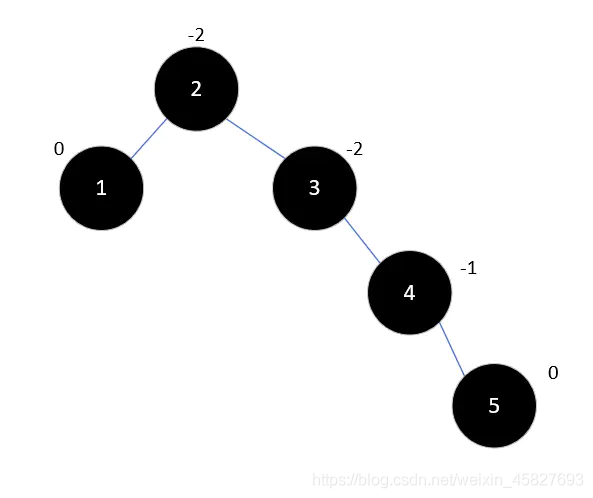
6.将其左旋：没什么大毛病，我们继续

7.在插入元素6，此时为最小不平衡子树

8.再将其左旋，这里具体怎么左旋，就这么想，就是在满足二叉排序树性质的同时，让根节点左边的深度增加，右子树的深度减小，以达到满足二叉平衡树的性质。

接下来的过程大家可以自行去尝试做出来

三、最终结果

可以看到，最后树的高度仅为4，比之前的8对比来说，效率就高了近一半。

平衡二叉树的删除操作与插入类似，这里将不再介绍。大家可以自己思考如何最高效地删除元素，可以分叶结点、仅有一个子结点和有两个子结点三种情况考虑，这里还用到了递归的思想。

到此这篇关于Java源码解析之平衡二叉树的文章就介绍到这了,更多相关Java平衡二叉树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • Java二叉树的四种遍历(递归和非递归)

    Java二叉树的四种遍历(递归和非递归)

    二叉树的遍历可以分为前序.中序.后序.层次遍历. 前中后是指何时访问中间节点,即前序遍历,遍历节点的顺序为:中->左->右: 中序遍历,遍历节点的顺序为:左->中->右: 后序遍历,遍历节点的顺序为:左->右->中. 前序遍历 递归实现 public void preorder_Traversal(TreeNode root) { if(root==null)return; //访问节点的逻辑代码块 System.out.print(root.val+" &q

  • java实现按层遍历二叉树

    本文实例为大家分享了java实现按层遍历二叉树,按层遍历二叉树可以通过队列来实现.其主要思路如下: 1.先将根节点放入队列中 2.每次都从队列中取出一个结点打印该结点的值 3.若这个结点有子结点,则将它的子结点放入队列尾,知道队列为空. 实现代码如下: import java.util.LinkedList; import java.util.Queue; public class LayerTranverse { //按层遍历二叉树 public static void main(String

  • JAVA二叉树的几种遍历(递归，非递归)实现

    JAVA二叉树的几种遍历(递归，非递归)实现

    首先二叉树是树形结构的一种特殊类型,它符合树形结构的所有特点.本篇博客会针对二叉树来介绍一些树的基本概念,二叉树的基本操作(存储,返回树的深度,节点个数,每一层的节点个数),二叉树的四种遍历(层次,先序,中序,后序) 一.基本概念 二叉树有5种基本形态: 注:二叉树有序树,就是说一个节点的左右节点是有大小之分的,我们通常设定为左孩子一定大于右孩子,下面的实现都是基于这个规则的.二叉树分为三种:满二叉树,完全二叉树,不完全二叉树 二叉树的四种遍历:层次,先序,中序,后序首先是非递归实现上图的满二叉

  • Java实现二叉树的深度优先遍历和广度优先遍历算法示例

    Java实现二叉树的深度优先遍历和广度优先遍历算法示例

    本文实例讲述了Java实现二叉树的深度优先遍历和广度优先遍历算法.分享给大家供大家参考,具体如下: 1. 分析 二叉树的深度优先遍历的非递归的通用做法是采用栈,广度优先遍历的非递归的通用做法是采用队列. 深度优先遍历:对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次.要特别注意的是,二叉树的深度优先遍历比较特殊,可以细分为先序遍历.中序遍历.后序遍历.具体说明如下: 先序遍历:对任一子树,先访问根,然后遍历其左子树,最后遍历其右子树. 中序遍历:对任一子树,先遍历其左子树,然

  • Java二叉树的遍历思想及核心代码实现

    Java二叉树的遍历思想及核心代码实现

    二叉树在计算机中的存储方式往往线性结构,线性存储分为顺序存储和链式存储,将二叉树按层序编号. 顺序结构:按编号的顺序进行存储,对于完全二叉树而言,顺序存储可以反映二叉树的逻辑,但是对于大多数的二叉树则无法反映其逻辑关系,不过可以用 ^ 来代替不存在的结点,但是如果这个树是一个右斜树,就非常浪费存储空间.所以二叉树的存储形式一般为链式存储结构. 链式存储:每一个结点都分有一个数据域(data)和两个指针域(lchild和rchild),指针域分别指向左孩子和右孩子,若为空则为null.遍历方式有四

  • Java实现的二叉树常用操作【前序建树，前中后递归非递归遍历及层序遍历】

    Java实现的二叉树常用操作【前序建树，前中后递归非递归遍历及层序遍历】

    本文实例讲述了Java实现的二叉树常用操作.分享给大家供大家参考,具体如下: import java.util.ArrayDeque; import java.util.Queue; import java.util.Stack; //二叉树的建树,前中后 递归非递归遍历 层序遍历 //Node节点 class Node { int element; Node left; Node right; public Node() { } public Node(int element) { this.

  • Java 最优二叉树的哈夫曼算法的简单实现

    Java 最优二叉树的哈夫曼算法的简单实现

    最优二叉树也称哈夫曼树,讲的直白点就是每个结点都带权值,我们让大的值离根近.小的值离根远,实现整体权值(带权路径长度)最小化. 哈夫曼算法的思想我认为就是上面讲的,而它的算法实现思路是这样的: 从根结点中抽出权值最小的两个(涉及排序,但是我这个实现代码没做严格的排序,只有比较)合并出新的根结点重新加入排序(被抽出来的两个自然是变成非根结点了啊),就这样循环下去,直到合并完成,我们得到一颗最优二叉树--哈夫曼树. 说明: (1)哈夫曼树有n个叶子结点,则我们可以推出其有n-1个分支结点.因此我在定

  • java实现二叉树遍历的三种方式

    本文实例为大家分享了java实现二叉树遍历的具体代码,供大家参考,具体内容如下 二叉树如下: 遍历结果如下: 以下是实现代码: package binTree; import java.util.Stack; /** * @author bin.zhang * @version 2017年8月29日 上午10:22:01 */ public class BinTreeTraversal { public static void main(String[] args) { System.out.p

  • Java实现二叉树的建立、计算高度与递归输出操作示例

    本文实例讲述了Java实现二叉树的建立.计算高度与递归输出操作.分享给大家供大家参考,具体如下: 1. 建立 递归输出 计算高度 前中后三种非递归输出 public class Tree_Link { private int save = 0; private int now = 0; Scanner sc = new Scanner(System.in); /* * 构造函数 */ Tree_Link(){ } /* * 链表建立 */ public Tree Link_Build(Tree

  • java二叉树的非递归遍历

    二叉树的递归遍历比较简单,这里就不聊了.今天主要聊聊二叉树的非递归遍历,主要借助于"栈"后进先出的特性来保存节点的顺序,先序遍历和中序遍历相对来说比较简单,重点理解后序遍历. 1. 先看看节点类型: //二叉树的节点类型 private class Node{ int data; //节点值 Node leftChild; //左孩子 Node rightChild; //右孩子 public Node(int data) { this.data=data; } } 2.先序遍历. 非

  • java编程题之从上往下打印出二叉树

    本文实例为大家分享了java从上往下打印出二叉树的具体代码,供大家参考,具体内容如下 github:剑指offer编程全部试题 import java.util.ArrayList; import java.util.Stack; /** * * 剑指offer编程题(JAVA实现)--第22题:从上往下打印出二叉树 * * 题目描述 * 从上往下打印出二叉树的每个节点,同层节点从左至右打印. * */ public class Test22 { ArrayList<Integer> arra

  • java编程求二叉树最大路径问题代码分析

    题目: Binary Tree Maximum Path Sum Given a binary tree, find the maximum path sum. The path may start and end at any node in the tree. For example: Given the below binary tree, 1 / \ 2 3 Return 6. 节点可能为负数,寻找一条最路径使得所经过节点和最大.路径可以开始和结束于任何节点但是不能走回头路. 这道题虽然

  • Java二叉树路径和代码示例

    给定一个二叉树,找出所有路径中各节点相加总和等于给定 目标值 的路径. 一个有效的路径,指的是从根节点到叶节点的路径. 样例 给定一个二叉树,和 目标值 = 5: 1 / \ 2 4 / \ 2 3 返回: [ [1, 2, 2], [1, 4] ] 代码如下: /** * Definition of TreeNode: * public class TreeNode { * public int val; * public TreeNode left, right; * public Tree

  • Java实现打印二叉树所有路径的方法

    本文实例讲述了Java实现打印二叉树所有路径的方法.分享给大家供大家参考,具体如下: 问题: 给一个二叉树,把所有的路径都打印出来. 比如,对于下面这个二叉树,它所有的路径为: 8 -> 3 -> 1 8 -> 2 -> 6 -> 4 8 -> 3 -> 6 -> 7 8 -> 10 -> 14 -> 13 思路: 从根节点开始,把自己的值放在一个数组里,然后把这个数组传给它的子节点,子节点同样把自己的值放在这个数组里,又传给自己的子节点,

  • java 对称二叉树的判断

    1. 题目描述 请实现一个函数,用来判断一颗二叉树是不是对称的.注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的. 2. 解题思路 可以按照类似层次遍历,来判断是否是堆成二叉树: 首先根节点以及其左右子树,左子树的左子树和右子树的右子树相同,以及左子树的右子树和右子树的左子树相同即可,然后采用递归一直判断下去. 3. 代码 public class isSymmetrical { public static void main(String[] args) { // 新建一棵二叉搜索

  • Java中二叉树的建立和各种遍历实例代码

    Java中二叉树的建立和各种遍历实例代码

    这是个常见的面试题,比如说通过二叉树的先序和中序遍历,得到二叉树的层序遍历等问题 先序+中序->建树 假设现在有个二叉树,如下: 此时遍历顺序是: PreOrder: GDAFEMHZ InOrder: ADEFGHMZ PostOrder: AEFDHZMG 现在给出先序(preOrder)和中序(InOrder),建立一颗二叉树 或者给出中序(InOrder)和后序(PostOrder), 建立二叉树,其实是一样的 树节点的定义: class Tree{ char val; Tree lef

  • java栈实现二叉树的非递归遍历的示例代码

    java栈实现二叉树的非递归遍历的示例代码

    一般来说遍历二叉树用到递归,但是用Stack进行遍历也是一个不错的方法. 二叉树设置 class Node{ public int val; public Node left; public Node right; public Node(int v) { val=v; left=null; right=null; } } public class Main { public static void main(String[] args) { Node head =new Node(0); No

  • java二叉树的几种遍历递归与非递归实现代码

    java二叉树的几种遍历递归与非递归实现代码

    前序(先序)遍历 中序遍历 后续遍历 层序遍历 如图二叉树: 二叉树结点结构 public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x){ val=x; } @Override public String toString(){ return "val: "+val; } } 访问函数 public void visit(TreeNode node){ System.out.print(

随机推荐