C语言线索二叉树基础解读

目录

• 线索二叉树的意义
• 线索二叉树的定义
• 线索二叉树结构的实现
• 二叉树的线索存储结构
• 二叉树的中序线索化
• 线索二叉树的中序遍历
• 总结

线索二叉树的意义

• 对于一个有n个节点的二叉树，每个节点有指向左右孩子的指针域。其中会出现n+ 1个空指针域，这些空间不储存任何事物，浪费着内存的资源。
• 对于一些需要频繁进行二叉树遍历操作的场合，二叉树的非递归遍历操作过程相对比较复杂，递归遍历虽然简单明了，但是会有额外的开销，对于操作的时间和空间都比较浪费。
• 我们可以考虑利用这些空地址，存放指向节点在某种遍历次序下的前驱和后继节点的地址。通过这些前驱和后继节点的地址可以知道，从当前位置下一步应该走向哪里。

线索二叉树的定义

• 指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应的二叉树就称为线索二叉树。
• 对二叉树以某种次序遍历使其变为线索二叉树的过程称为线索化。

线索二叉树结构的实现

二叉树的线索存储结构

为了区分二叉树某一节点是指向它的孩子节点还是指向前驱或者后继节点，我们可以在每个节点增设两个标志，Ltag，Rtag.

其中:

• Ltag为0时，代表该节点指向它的左孩子，Ltag为1时，代表该节点指向它的前驱节点。
• Rtag为0时，代表该节点指向它的右孩子，Rtag为1时，代表该节点指向它的后继节点。

所以，线索二叉树结构定义代码如下：

typedef char BTDataType;
typedef enum{Link,Thread}PointerTag;//Link 是0，Thread 是1。
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	PointerTag LTag ;
	PointerTag RTag;
	BTDataType data;
}BTNode;

二叉树的中序线索化

线索化的过程就是在遍历过程中修改空指针的过程

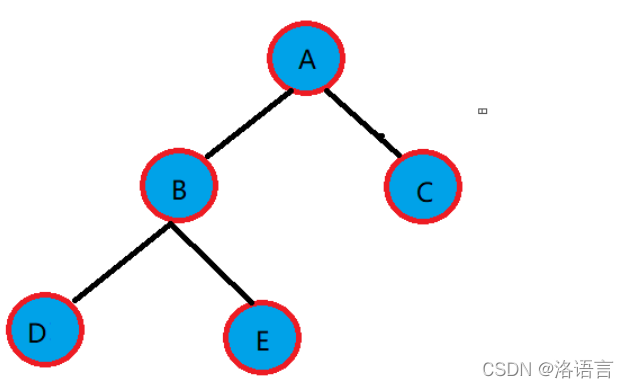
以上二叉树中序遍历可以得到：

D B E A F C
  D的前驱是空，后继是B
  B的前驱是D，后继是E
  E的前驱是B，后继是A
  F的前驱是A，后继是C
  C的前驱是F，后继是空

线索化后：

中序遍历线索化的递归函数代码如下：

//中序线索化
BTNode* pre = NULL;/*全局变量，始终指向刚刚访问过的节点*/
void InThreading(BTNode* p)
{
	if (p == NULL) return;
	InThreading(p->left);//递归左子树线索化
	if (!p->left)//左孩子为空，left指针指向前驱
	{
		p->LTag = Thread;
		p->left = pre;
	}
	if (pre!=NULL && !pre->right)//右孩子为空，right指针指向后继指针。
	//这里判断 pre!=NULL 是因为线索化中序遍历的第一个节点(节点D)时，它并没有前驱节点，此时的pre仍然是NULL。
	{
		pre->RTag = Thread;
		pre->right = p;
	}
	pre = p;//保持pre指向p的前驱
	InThreading(p->right);
}

分析：

• if (!p->left)表示如果某节点的左指针域为空，因为其前驱节点刚刚访问过，并且赋值给了pre，所以可以将pre赋值给 l -> left，并且修改 p-> LTag = Thread，以完成前驱节点的线索化。
• pre 是 p 的前驱，那么， p 就是 pre 的后继。当pre -> right 为空时，就可以将p赋值给 pre -> right ， 并且修改 pre -> RTag = Thread。

线索二叉树的中序遍历

void MidOrder(BTNode*p)
{
	while (p != NULL)
	{
		while (p->LTag == Link)//
		{
			p = p->left;
		}
		printf("%c ",p->data);
		while (p->RTag == Thread && p->right != p)
		{
			p = p->right;
			printf("%c ", p->data);
		}
		p = p->right;
	}
	return;
}

分析：

• while (T->ltag == Link)从根节点开始遍历，如果左标记是Link让它一直循环下去，直到找到标记为Thread的的结点，也就是要遍历的第一个结点，然后根据后驱指针找到后继结点
• 后面就是重复以上过程，直到遍历完整个二叉数。

总结

如果所用的二叉数需要经常遍历或查找结点时需要某种遍历序列中的前驱和后继，那么采用线索二叉数是一个很好的选择；

以上内容参考于《大话数据结构》。

到此这篇关于C语言线索二叉树基础解读的文章就介绍到这了,更多相关C语言线索二叉树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！