Java快速排序与归并排序及基数排序图解示例

目录

• 一、快速排序
• 1、基本介绍
• 2、代码实现
• 二、归并排序
• 1、基本介绍
• 2、代码实现
• 三、基数排序
• 1、基本介绍
• 2、代码实现

一、快速排序

1、基本介绍

以上面的数组为例分析快速排序。

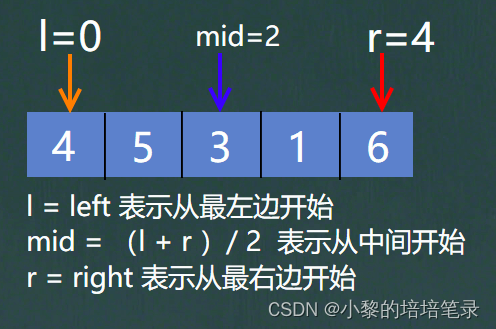
首先要传入三个值，数组arr[ ] ，最左边下标left ，最右边下标 right。然后将根据左右的下标值计算出中间值mid。

我们要做的就是将左边的值大于mid的放到右边，将右边小于mid的值放到左边。

左右两边分别单独循环，左边找到比mid大的数，右边找到比mid小的数。

两边分别找到符合条件的数后，进行交换。

然后继续比较并交换，此刻 l 和 mid 都指向3，r 指向 5 。

这时需要进行判断，如果arr[l] 等于mid 则 r--，如果arr[r] 等于mid则 l++ 。此时又进行判断arr[l] 是否等于arr[r]，等于则退出。第一轮就结束了。

第一次完以后，我们使用递归，递归会重复上面的操作，从而完成排序。

2、代码实现

//参数传入数组arr ， 最左边的下标left，最右边的下标 right
public static void quickSort(int[] arr , int left , int right){
        //分别用临时变量代替
        int l = left;
        int r = right;
        //中间的下标
        int middle = arr[(left + right) / 2];
        //临时变量，用于交换数据
        int temp = 0;
        //进行循环，只要右边的下标 l 小于 左边的下标 r 就进行循环
        while (l < r){
            //左边l 到 中间middle 单独循环，找到比middle大的值
            while (arr[l] < middle){
                l += 1;
            }
            //中间middle 到 右边 r 单独循环，找到比middle小的值
            while (arr[r] > middle){
                r -= 1;
            }
            //退出循环，表示找到，不过先判断 l 是否大于等于 r
            //满足就可以退出循环，不需要执行下面的代码了
            if(l >= r){
                break;
            }
            //找到的数据进行交换
            temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;
            //此时进行判断，如果arr[l] 等于middle  则 r--
            if(arr[l] == middle){
                r -= 1;
            }
            //如果  arr[r] 等于middle 则 l++
            if(arr[r] == middle){
                l += 1;
            }
        }
        //退出循环，l 会等于 r，此时要将两者移位，l进行加一，r进行减一
        if(l == r){
            l += 1;
            r -= 1;
        }
        //第一轮完成后进行递归
        //重复上面的方法，向左递归
        if(left < r){
            //r 继续往前移的，所以左下标为left ，右下标为 r
            quickSort(arr, left , r);
        }
        //重复上面的操作，向右递归
        if(right > l){
            //l 继续往后移的，所以左下标为 l ，右下标为 right
            quickSort(arr, l , right);
        }
    }

二、归并排序

1、基本介绍

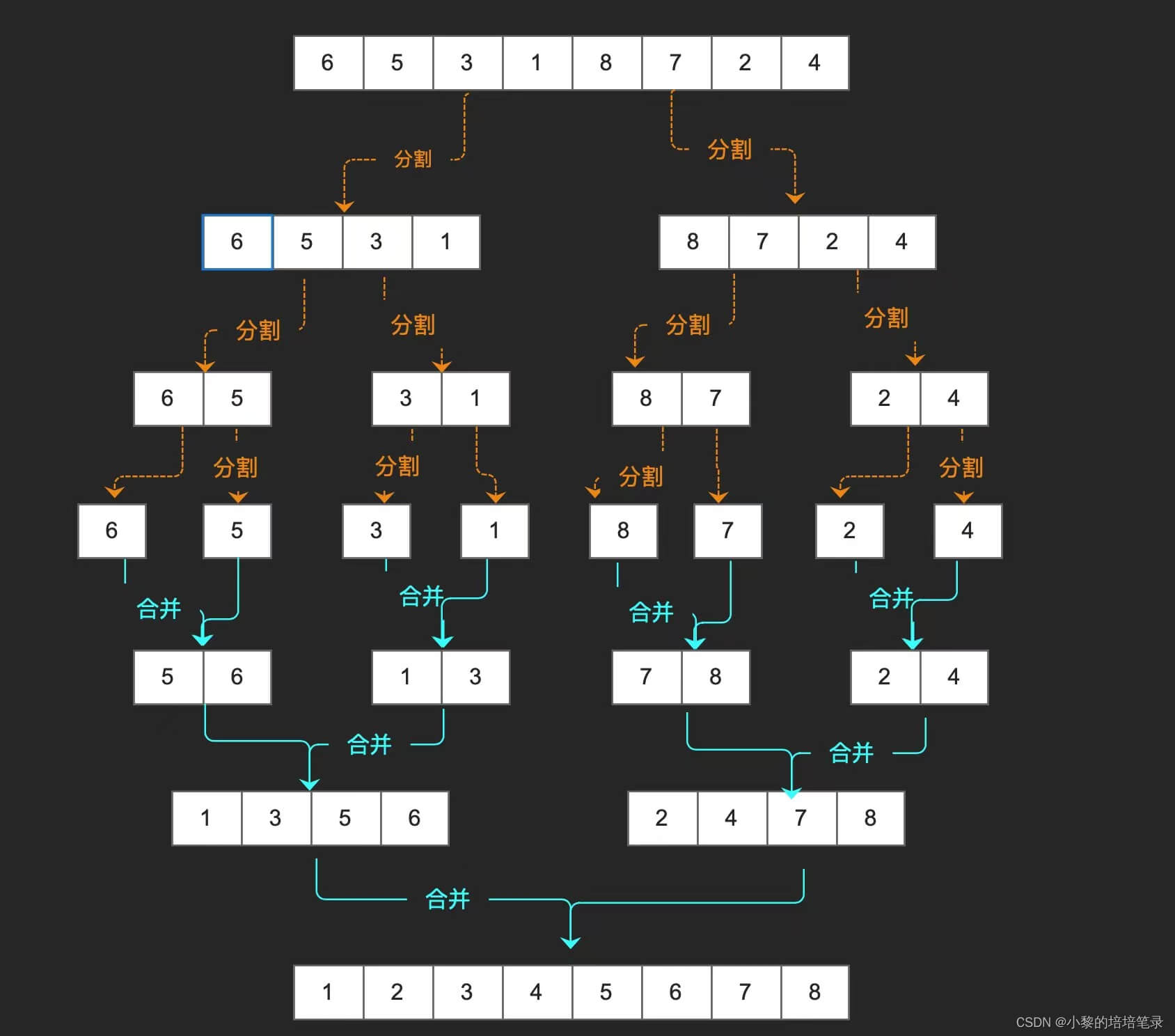
2、代码实现

首先实现合并

public static void merger(int[] arr , int left ,int mid , int right , int[] temp){
        int i = left;
        int j = mid + 1;
        int t = 0;//数组temp的下标
        //将arr数组按顺序放入temp 数组
        while (i <= mid  && j <= right){
            //从中间分隔开，左边和右边相互比较
            //如果左边更小，先放入temp数组，否则右边先放入
            if(arr[i] < arr[j]){
                temp[t] = arr[i];
                i++;
                t++;
            }else {
                temp[t] = arr[j];
                j++;
                t++;
            }
        }
        //有可能有一边还没放完，于是继续循环放放入
        //左边没放完
        while (i <= mid){
            temp[t] = arr[i];
            t++;
            i++;
        }
        //右边没放完
        while (j <= right){
            temp[t] = arr[j];
            j++;
            t++;
        }
        //将temp中数据拷入到arr
        t = 0;
        int leftind = left;
        //第一次（leftind，right）是（0,1）（2,3）（4,5）（6,7）
        //第二次（leftind，right）是（0,3）（4,7）
        //第三次（leftind，right）是（0,7）
        while (leftind <= right){
            arr[leftind] = temp[t];
            t++;
            leftind++;
        }
    }

分隔和合并进行递归

public static void mergerSort(int[] arr, int left,int right, int[] temp){
        //判断
        if (left < right){
            //求出中间值
            int mid = (left + right) / 2;
            //调用自己，向左递归
            mergerSort(arr, left, mid , temp);
            //调用自己，向右递归
            mergerSort(arr , mid + 1, right, temp);
            //调用merger进行合并
            merger(arr, left , mid, right, temp);
        }
    }

三、基数排序

1、基本介绍

首先我们需要10个数组，分别对应10个桶，每个桶有对应的下标。

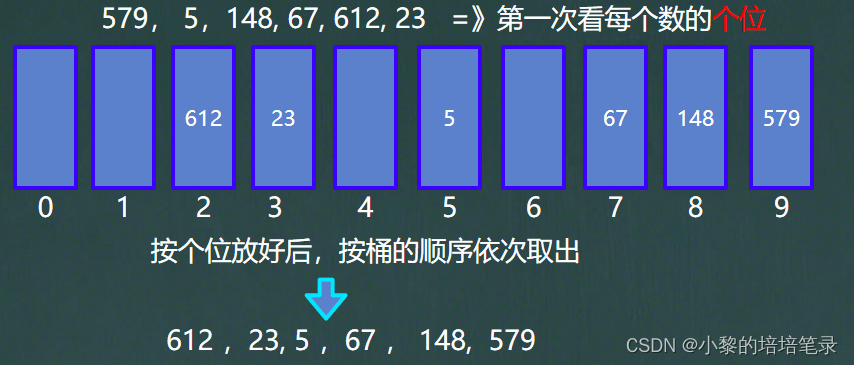
然后按每个数的个位数大小放入对应的桶中，放好后，按桶的顺序依次取出。

第二次是看每个数的十位，不及十位的就当做0，依旧是依次放入对应的桶中，并按顺序取出。

第三次是看每个数的百位，重复上面的操作，最后得到的就是有序的数组。

2、代码实现

public static void cardinalitySort(int[] arr){
        //首先找到数组中最大数的位数
        int max = arr[0];
        for(int i = 1; i < arr.length - 1; i++ ){
            if(arr[i] > max){
                max = arr[i];
            }
        }
        int maxLength = (max + "").length();
        //定义10个桶，每个桶大小为数组大小
        int[][] bucket = new int[10][arr.length];
        //定义一个数组来表示每个桶存放的数据
        int[] bucketcount = new int[10];
        //n是用来进行位数处理的
        for(int i = 1, n = 1; i <= maxLength ; i++,n *= 10){
            for(int j = 0; j < arr.length ; j++){
                //对每位数进行位处理，并放入桶中
                int elentData = arr[j] / n % 10;
                /*
                  放对应的桶中,
                  bucketcount[elentData]表示对应的桶的数据,
                  假如第一个数为579，要放入bucketcount[9]（第九个桶）的第一个位置，
                  默认初始化为0，所以第一个数放入的位置是bucketcount[9] = 0
                */
                bucket[elentData][bucketcount[elentData]] = arr[j];
                //第一个数放完后，这个桶中数据进行++，
                //下次再放入这个桶时，bucketcount[9] = 1
                bucketcount[elentData]++;
            }
            int index = 0;
            //遍历每一个桶
            for(int k = 0; k < bucketcount.length; k++){
                //第一次默认为bucketcount[k] = 0
                //所以如果第一个数为零，就说明这个桶为空
                if(bucketcount[k] != 0){
                    //有数据，则桶bucketcount[k]就会有对应数据多少的大小，进行遍历
                    for(int l = 0; l < bucketcount[k] ; l++){
                        //放入原来的数组
                        arr[index++] = bucket[k][l];
                    }
                }
                //桶中的数放回原数组放完后，进行置空
                bucketcount[k] = 0;
            }
        }
    }

到此这篇关于Java快速排序与归并排序及基数排序图解示例的文章就介绍到这了,更多相关Java快速排序内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！