详解JavaScript树结构

对于数据结构“树”，想必大家都熟悉，今儿，我们就再来回顾一下数据结构中的二叉树与树，并用JavaScript实现它们。

ps:树结构在前端中，很多地方体现得淋漓尽致，如Vue的虚拟DOM以及冒泡等等。

二叉树

--概念--

二叉树是一种树形结构，它的特点是每个结点至多只有两棵子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

如下，就是一棵二叉树（注：下文二叉树相关例子，都以该二叉树为例）：

且，遍历二叉树（traversing binary tree）有三种常用方式，如下：

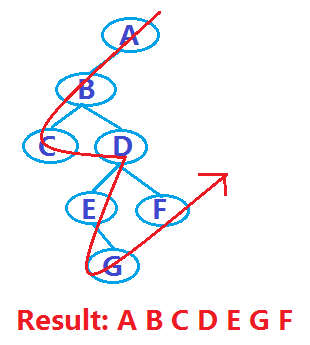
1）、先序遍历二叉树 （根左右）  

若二叉树为空，则空操作；否则

--访问根结点；

--先序遍历左子树；

--先序遍历右子树。

例如，上述例子中的二叉树，遍历结果如下：

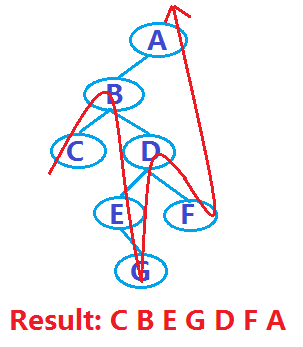
2）、中序遍历二叉树（左根右）

若二叉树为空，则空操作；否则

--中序遍历左子树；

--访问根结点；

--中序遍历右子树。

例如，上述例子中的二叉树，遍历结果如下：

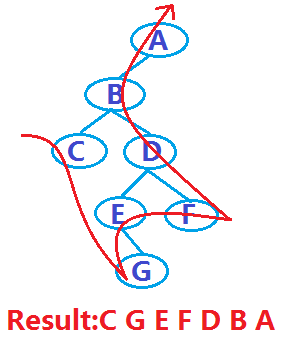
3）、后序遍历二叉树（左右根）

若二叉树为空，则空操作；否则

--后序遍历左子树；

--后序遍历右子树；

--访问根结点。

例如，上述例子中的二叉树，遍历结果如下：

好了，了解了二叉树以及遍历方式，那么，接下来我们就一起用JavaScrip来实现下吧，当然采用链式存储结构。

首先，利用JavaScript构造函数建立二叉树结点，如下：

function TreeNode(){
 this.data = null;//该节点数据
 this.lchild = null;//左子树
 this.rchild = null;//右子树
};

然后，我们可以通过遍历二叉树的算法，构建一棵二叉树，如下，采用先序序列建立一棵二叉树方法：

/*
*method:采用先序序列建立二叉树
*@params: nodeList（Array） --树节点，以先序序列存入数组中，null代表空节点
*/
TreeNode.createBiTree = function(nodeList){
 var i = 0;
 return (function getNode(){
  var node = null,
   val = nodeList[i++];
  if(!val){
   node = null;
  }else{
   node = new TreeNode();
   node.data = val;
   node.lchild = getNode();
   node.rchild = getNode();
  }
  return node;
 })();
};

最后，就是遍历一棵二叉树咯，分别为先序遍历（PreOrderTraverse）、中序遍历（InOrderTraverse）以及后序遍历（PostOrderTraverse），如下：

TreeNode.prototype = {
 constructor: TreeNode,
 _PreOrderTraverse: function(node){
  if(node){
   console.log(node.data);
   this._PreOrderTraverse(node.lchild);
   this._PreOrderTraverse(node.rchild);
  }
 },
 PreOrderTraverse: function(){
  console.log('PreOrder:');
  this._PreOrderTraverse(this);
 },
 _InOrderTraverse: function(node){
  if(node){
   this._InOrderTraverse(node.lchild);
   console.log(node.data);
   this._InOrderTraverse(node.rchild);
  }
 },
 InOrderTraverse: function(){
  console.log('InOrder:');
  this._InOrderTraverse(this);
 },
 _PostOrderTraverse: function(node){
  if(node){
   this._PostOrderTraverse(node.lchild);
   this._PostOrderTraverse(node.rchild);
   console.log(node.data);
  }
 },
 PostOrderTraverse: function(){
  console.log('PostOrder:');
  this._PostOrderTraverse(this);
 }
};

好了，利用上述二叉树例子，我们可以自行测试下：

var treeNode = null,
 nodeList = ['A', 'B', 'C', null, null, 'D', 'E', null, 'G', null, null, 'F', null, null, null];
//getting a binary tree from nodeList
treeNode = TreeNode.createBiTree(nodeList);
//traversing the tree of treeNode
treeNode.PreOrderTraverse();//ABCDEGF
treeNode.InOrderTraverse();//CBEGDFA
treeNode.PostOrderTraverse();//CGEFDBA

树

--概念--

树是n（n>=0）个结点的有限集。在任意一棵非空树中，有且仅有一个特定的称为根（root）的结点，当n>1时，其余结点可分为m（m>0）个互不相交的有限集，其中每个集合本身又是一棵树，称为根的子树。当然，二叉树肯定属于树咯。

如下，就是一棵树（注：下文树的相关例子，都以该树为例）：

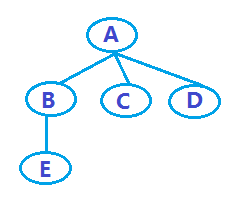
且，遍历一棵多孩子树，有两种常用遍历方式，如下：

1) 、先根遍历，和深度优先搜索（Depth_First Search）遍历类似。都是利用栈来遍历元素，如下：

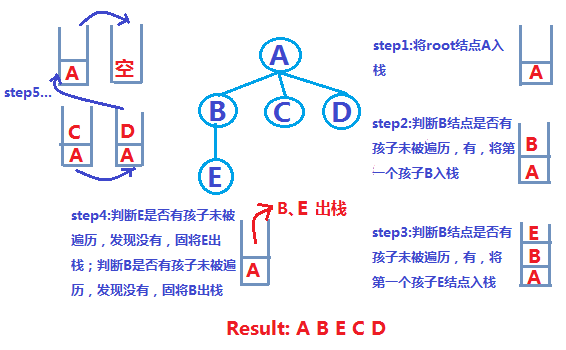
2) 、按层次遍历，和广度优先搜索（Breadth_First Search）遍历类似。都是利用队列来遍历元素，如下：

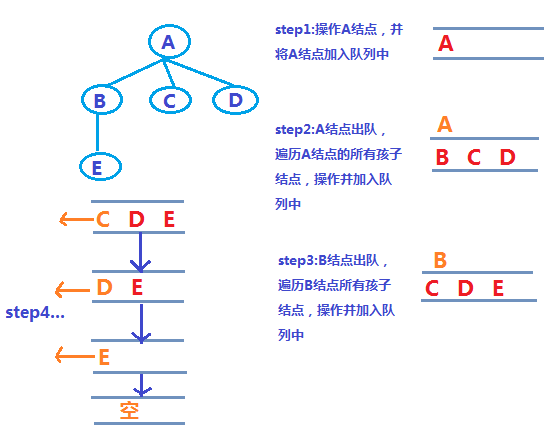
好了，了解了树以及遍历方式，那么，接下来我们就一起用JavaScrip来实现下吧，当然也是采用链式存储结构。

首先，利用JavaScript建立树结点，如下：

/*
*@Params: data --节点数据
   children -- 所有孩子结点
*/
function TreeNode(data, children){
 if(!(this instanceof TreeNode)){
  return new TreeNode(data, children);
 }
 this.data = data || null;
 this.children = children || [];
};

根据上述TreeNode构造函数，我们可以将例子中的树，表示如下：

var treeNode = TreeNode('A', [
       TreeNode('B', [TreeNode('E')]),
       TreeNode('C'),
       TreeNode('D')
     ]);

接着，就是编写遍历树方法咯，分别为先根遍历和按层次遍历，如下：

TreeNode.prototype = {
 constructor: TreeNode,
 _traverseAsDFS: function(node){//先根遍历
  var self = this;
  if(node){
   console.log(node.data);
   node.children.forEach(function(child){
    if(child.children.length){
     self._traverseAsDFS(child);
    }else{
     console.log(child.data);
    }
   });
  }
 },
 traverseAsDFS: function(){
  console.log('Depth_First Search');
  this._traverseAsDFS(this);
 },
 traverseAsBFS: function(){//按层次遍历
  var queue = [];
  console.log('Breadth_First Search');
  console.log(this.data);
  if(this.children.length){
   queue.push(this);
  }
  while(queue.length){
   let tempNode = queue.shift();
   tempNode.children.forEach(function(child){
    console.log(child.data);
    if(child.children.length){
     queue.push(child);
    }
   });
  }
 }
};

好了，利用上述二叉树例子，我们可以自行测试下：

var treeNode = TreeNode('A', [
       TreeNode('B', [TreeNode('E')]),
       TreeNode('C'),
       TreeNode('D')
     ]);
treeNode.traverseAsDFS();//ABECD
treeNode.traverseAsBFS();//ABCDE

关于上述全部代码，见github。

以上就是本文的全部内容，希望本文的内容对大家的学习或者工作能带来一定的帮助，同时也希望多多支持我们！