详解基于C++实现约瑟夫环问题的三种解法

目录

• 一、前言
• 二、循环链表模拟
• 三、有序集合模拟
• 四、递归公式解决
• 五、结语

一、前言

什么是约瑟夫环问题？

约瑟夫环问题在不同平台被"优化"描述的不一样，例如在牛客剑指offer叫孩子们的游戏，还有叫杀人游戏，点名……最直接的感觉还是力扣上剑指offer62的描述：圆圈中最后剩下的数字。

问题描述：

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

当然，这里考虑m，n都是正常的数据范围，其中

• 1 <= n <= 10^5
• 1 <= m <= 10^6

对于这个问题，你可能脑海中有了印象，想着小时候村里一群孩子坐在一起，从某个开始报数然后数到几出列，下一个重新开始一直到最后一个。

二、循环链表模拟

这个问题最本质其实就是循环链表的问题，围成一个圈之后，就没有结尾这就是一个典型的循环链表嘛！一个一个顺序报数，那不就是链表的遍历枚举嘛！数到对应数字的出列，这不就是循环链表的删除嘛！

并且这里还有非常方便的地方：

• 循环链表的向下枚举不需要考虑头尾问题，直接node=node.next向下
• 循环聊表的删除也不需要考虑头尾问题，直接node.next=node.next.next删除

当然也有一些需要注意的地方

• 形成环形链表很简单，只需要将普通链表的最后一个节点的next指向第一个节点即可
• 循环链表中只有一个节点的时候停止返回，即node.next=node的时候
• 删除，需要找到待删除的前面节点，所以我们删除计数的时候要少即一位，利用前面的那个节点直接删除后面节点即可

这样，思路明确，直接开撸代码：

class Solution {
    class node//链表节点
    {
        int val;
        public node(int value) {
            this.val=value;
        }
        node next;
    }
    public int lastRemaining(int n, int m) {
        if(m==1)return n-1;//一次一个直接返回最后一个即可
        node head=new node(0);
        node team=head;//创建一个链表
        for(int i=1;i<n;i++)
        {
            team.next=new node(i);
            team=team.next;
        }
        team.next=head;//使形成环
        int index=0;//从0开始计数
        while (head.next!=head) {//当剩余节点不止一个的时候
            //如果index=m-2 那就说明下个节点(m-1)该删除了
            if(index==m-2)
            {
                head.next=head.next.next;
                index=0;
            }
            else {
                index++;
            }
            head=head.next;
        }
        return head.val;
    }
}

当然，这种算法太复杂了，大部分的OJ你提交上去是无法AC的，因为超时太严重了，具体的我们可以下面分析。

三、有序集合模拟

上面使用链表直接模拟游戏过程会造成非常严重非常严重的超时，n个数字，数到第m个出列。因为m如果非常大远远大于m，那么将进行很多次转圈圈。

所以我们可以利用求余的方法判断等价最低的枚举次数，然后将其删除即可，在这里你可以继续使用自建链表去模拟，上面的while循环以及上面只需添加一个记录长度的每次求余算圈数即可：

int len=n;
while (head.next!=head) {
  if(index==(m-2)%len)
  {
    head.next=head.next.next;
    index=0;
    len--;
  }
  else {
    index++;
  }
  head=head.next;
}

但我们很多时候不会手动去写一个链表模拟，我们会借助ArrayList和LinkedList去模拟，如果使用LinkedList其底层也是链表，使用ArrayList的话其底层数据结构是数组。不过在使用List其代码方法一致。

List可以直接知道长度，也可删除元素，使用List的难点是一个顺序表怎们模拟成循环链表？

咱们仔细思考：假设当前长度为n，数到第m个(通过上面分析可以求余让这个有效的m不大于n)删除，在index位置删除。那么删除后剩下的就是n-1长度，index位置就是表示第一个计数的位置，我们可以通过求余得知走下一个删除需要多少步，那么下个位置怎么确定呢？

你可以分类讨论看看走的次数是否越界，但这里有更巧妙的方法，可以直接求的下一次具体的位置，公式就是为：

index=(index+m-1)%(list.size());

因为index是从1计数，如果是循环的再往前m-1个就是真正的位置，但是这里可以先假设先将这个有序集合的长度扩大若干倍，然后从index计数开始找到假设不循环的位置index2，最后我们将这个位置index2%(集合长度)即为真正的长度。

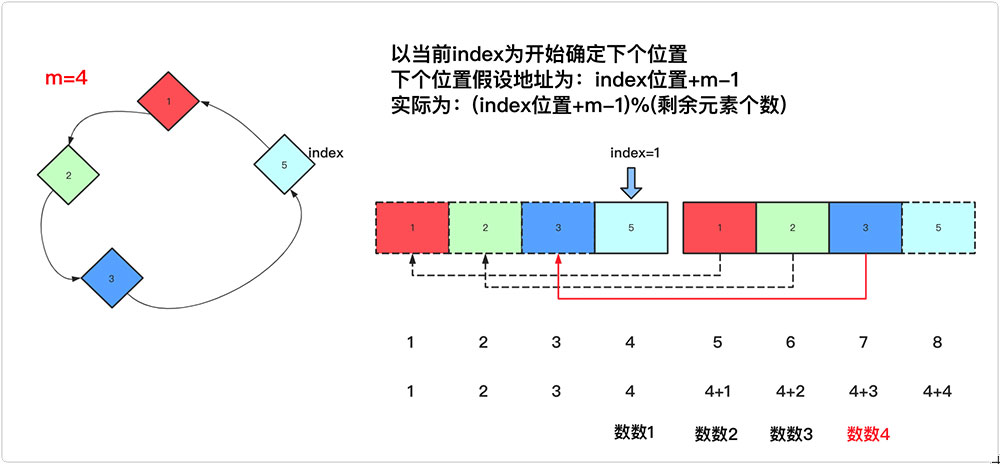
使用这个公式一举几得，既能把上面m过大循环过多的情况解决，又能找到真实的位置，就是将这个环先假设成线性的然后再去找到真的位置，如果不理解的话可以再看看这个图：

这种情况的话大部分的OJ是可以勉强过关的，面试官的层面也大概率差不多的，具体代码为：

class Solution {
    public int lastRemaining(int n, int m) {
        if(m==1)
            return n-1;
        List<Integer>list=new ArrayList<>();
        for(int i=0;i<n;i++)
        {
            list.add(i);
        }
        int index=0;
        while (list.size()>1)
        {
            index=(index+m-1)%(list.size());
            list.remove(index);
        }
        return list.get(0);
    }
}

四、递归公式解决

我们回顾上面的优化过程，上面用求余可以解决m比n大很多很多的情况(即理论上需要转很多很多圈的情况)。但是还可能存在n本身就很大的情况，无论是顺序表ArrayList还是链表LinkedList去频繁查询、删除都是很低效的。

所以聪明的人就开始从数据找一些规律或者关系。

先抛出公式：

f(n,m)=(f(n-1,m)+m)%n

f(n,m)指n个人，报第m个编号出列最终编号

下面要认真看一下我的分析过程：

我们举个例子，有0 1 2 3 4 5 6 7 8 9十个数字，假设m为3,最后结果可以先记成f(10,3)，即使我们不知道它是多少。

当进行第一次时候，找到元素2 删除，此时还剩9个元素，但起始位置已经变成元素3。等价成3 4 5 6 7 8 9 0 1这9个数字重写开始找。

此时这个序列最终剩下的一个值即为f(10,3)，这个序列的值和f(9,3)不同，但是都是9个数且m等于3，所以其删除位置是相同的，即算法大体流程是一致的，只是各位置上的数字不一样。所以我们需要做的事情是找找这个序列上和f(9,3)值上有没有什么联系。

寻找过程中别忘记两点，首先可通过%符号对数字有效扩充，即我们可以将3 4 5 6 7 8 9 0 1这个序列看成(3,4,5,6,7,8,9,10,11)%10.这里的10即为此时的n数值。

另外数值如果是连续的，那么最终一个结果的话是可以找到联系的(差值为一个定制)。所以我们可以就找到f(10,3)和f(9,3)值之间结果的关系，可以看下图：

所以f(10,3)的结果就可以转化为f(9,3)的表达,后面也是同理：

f(10,3)=(f(9,3)+3)%10

f(9,3)=(f(8,3)+3)%9

……

f(2,3)=(f(1,3)+3)%2

f(1,3)=0

这样，我们就不用模拟操作，可以直接从数值的关系找到递推的关系，可以轻轻松松的写下代码：

class Solution {
    int index=0;
    public int lastRemaining(int n, int m) {
         if(n==1)
            return 0;
        return (lastRemaining(n-1,m)+m)%n;
    }
}

但是递归效率因为有个来回的规程，效率相比直接迭代差一些，也可从前往后迭代：

class Solution {
    public int lastRemaining(int n, int m) {
        int value=0;
            for(int i=1;i<=n;i++)
            {
                value=(value+m)%i;
            }
            return  value;
    }
}

五、结语

我想，通过本篇文章你应该掌握和理解了约瑟夫环问题，这种裸的约瑟夫环问题出现的概率很大，考察很频繁，链表模拟是根本思想，有序集合模拟链表是提升，而公式递推才是最有学习价值的地方，如果你刚开始接触不理解可以多看几遍。

以上就是详解基于C++实现约瑟夫环问题的三种解法的详细内容，更多关于C++ 约瑟夫环的资料请关注我们其它相关文章！