C语言平衡二叉树真题练习

目录

• 一、题目描述
• 二、解题思路
• 自顶向下的递归（暴力解法）
• 自底向上的递归（最优解法）

题目难度：简单

LeetCode链接：平衡二叉树

一、题目描述

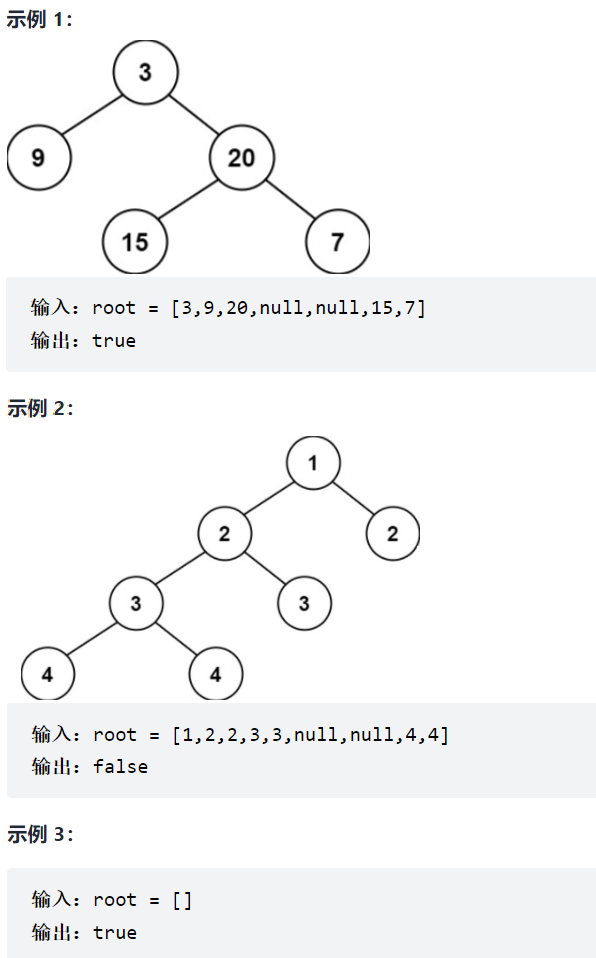
给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树 每个节点 的左右两个子树的高度差的绝对值不超过 1 。

二、解题思路

一棵二叉树是平衡二叉树，当且仅当其所有子树也都是平衡二叉树，因此我们使用递归的方式依次判断其所有子树是否为平衡二叉树，就知道这棵二叉树是不是平衡二叉树了。

自顶向下的递归（暴力解法）

自顶向下类似于 前序遍历，先判断当前树是否平衡，再判断当前树的左右子树是否平衡。

核心思路

写两个函数：

子函数：计算当前任意一个节点(树) root 的高度 root 是空节点：Depth ( root ) = 0root 是非空节点：Depth ( root ) = max ( Depth ( root->left ) , Depth ( root->right ) ) + 1

主函数：依次递归遍历完 root 的所有子树，对于「当前遍历到的子树」，判断是否平衡，首先计算其左右子树的高度，然后判断高度差是否不超过 1

• 如果不超过，才能继续往下递归遍历「当前树的左右子树」，判断其是否平衡；
• 如果超过1，说明不满足平衡条件，则直接返回 false，不用往下递归了。

递归过程演示：自顶向下的递归类似于前序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// 计算当前任意一个节点(树)的高度（子函数）
int TreeDepth(struct TreeNode* root)
{
    // 当前节点为空
    if(root == NULL)
    {
        return 0;
    }
    // 当前节点不为空，分别计算它的左右子树的高度
    int leftDepth = TreeDepth(root->left);
    int rightDepth = TreeDepth(root->right);
    // 当前节点(树)的高度
    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
bool isBalanced(struct TreeNode* root){
    // 依次递归遍历完root的所有子树，分别判断当前子树是否为高度平衡二叉树
    // 当前树的根节点为空，说明其满足高度平衡的二叉树，返回true
    if(root == NULL)
    {
        return true;
    }
    // 当前树的根节点不为空，分别计算它左右子树的高度
    int leftDepth = TreeDepth(root->left);
    int rightDepth = TreeDepth(root->right);
    // 计算左右子树的高度差
    int ret = leftDepth > rightDepth ? leftDepth - rightDepth : rightDepth - leftDepth;
    // 高度差不超过1，才能继续往下递归遍历当前树的左右子树
    return ret <= 1 && isBalanced(root->left) && isBalanced(root->right);
}

复杂度分析：

• 时间复杂度：O(n2)，其中 n 是二叉树中的节点个数。

最坏情况下，二叉树是满二叉树，主函数 isBalanced(root) 需要遍历二叉树中的所有节点，时间复杂度是 O(n)。计算每个子树的最大高度函数 TreeDepth(root) 被重复调用。除了根节点，其余所有节点都会被遍历两次，复杂度为 O[2(n-1)]，所以时间复杂度为 n*2(n-1) ≈ n2。

• 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。

自底向上的递归（最优解法）

方法一自顶向下递归，类似 前序遍历，先判断当前树是否平衡，再判断当前树的左右子树是否平衡，所以对于同一个节点，函数 TreeDepth 会被重复调用，会重复计算很多次子树的高度，导致时间复杂度较高。

如果使用自底向上的做法，则对于每个节点，函数 TreeDepth 只会被调用一次。因为到达左子树底部后，每次对应的左子树都是放在递归调度中的，每次只需要获取新的右子树长度便可。

自底向上递归类似于 后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。

• 如果当前树的左/右子树中只要有一个不平衡，则整个树就不平衡，返回-1（表示不平衡）
• 如果当前树是平衡的，则返回其高度，否则返回 -1（表示不平衡）。

写递归算法需要关注什么？

• 整个递归的终止条件：递归应该在什么时候结束？— 子树根节点为空的时候，空树也是平衡二叉树。
• 本级递归应该做什么？ — 判断当前树的左子树、右子树、以及当前树是否是平衡的。
• 返回值：应该返回给上一级的返回值是什么？— 当前树是平衡的，则返回其高度，不平衡则返回 -1。

递归算法流程：

每一级递归时，在我们眼中，当前树就是这样的，只有 root、left、right 三个节点。

到叶子节点了，当前树根节点 root 为空，说明是平衡的，则返回高度 0；

当前树根节点 root 不为空，计算左右子树 left 和 right 的高度，并判断：

• 如果「左子树 left 高度为 -1」、或「右子树 right 高度为 -1」、或「左右子树高度差 > 1」，说明整个树 不平衡 ，直接返回 -1（表示不平衡）。
• 如果不满足上面 3 种情况，说明当前树是 平衡 的，返回当前树的高度，即 max ( left, right ) + 1 。

补充：计算绝对值的函数：int abs( int n ); ，头文件 <stdlib.h> or <math.h>。

递归过程演示：自底向上递归类似于后序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// 计算当前树的高度，并判断当前树是否是平衡二叉树
int _isBalanced(struct TreeNode* root)
{
    // 先分别判断当前树的左/右子树是否平衡
    // 如果当前树的左/右子树中只要有一个不平衡，则全树就不平衡，返回-1（表示不平衡）
    // 如果当前树的左右子树都平衡，则继续判断当前树是否平衡
    // 1. 到叶子节点了，当前树根节点为空，说明是平衡的，则返回高度0
    if(root == NULL)
    {
        return 0;
    }
    // 2. 当前树根节点不为空
    // 计算左右子树的高度
    int leftTreeDepth = _isBalanced(root->left);
    int rightTreeDepth = _isBalanced(root->right);
    // 不平衡的3种情况：左子树高度为-1，右子树高度为-1，左右子树高度差>1
    if(leftTreeDepth == -1 || rightTreeDepth == -1 || abs(leftTreeDepth - rightTreeDepth) > 1)
    {
        return -1;
    }
    // 如果不满足上面3种情况，说明当前树是平衡的，返回当前树的高度
    return leftTreeDepth > rightTreeDepth ? leftTreeDepth + 1 : rightTreeDepth + 1;
}
bool isBalanced(struct TreeNode* root){
    // 递归遍历过程中：
    // 只要有一个子树高度为-1，说明整个树是不平衡的，返回false
    // 所有子树高度都不等于-1，说明整个树是平衡的，返回true
    return _isBalanced(root) != -1;
}

复杂度分析：

1.时间复杂度：O(n)，其中 n 是二叉树中的节点个数。

最坏情况是二叉树为满二叉树时，需要遍历完满二叉树中的所有节点，自底向上方法，因此每个节点只会被遍历一次，所以时间复杂度是 O(n)。

2.空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度却决于递归调用的层数，有 n 个节点的二叉树为单边树时深度最大，为 n。

到此这篇关于C语言平衡二叉树真题练习的文章就介绍到这了,更多相关C语言平衡二叉树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！