C语言数据结构图的创建与遍历实验示例

目录

• 一、 实验目的
• 二、 实验内容
• 三、 实验工具
• 四、 实验代码
• 五、 实验结果
• 六、总结与思考

一、 实验目的

理解图的基本概念，掌握图的存储结构，实现图的深度优先搜索遍历算法与广度优先搜索遍历算法。

二、 实验内容

利用邻接矩阵描述示例图，编写程序输出示例图的深度优先搜索和广度优先搜索的遍历序列。

具体步骤如下：

• 将图的邻接矩阵描述为一个二维数组，并将该数组定义为全局变量，以便数据的传递；
• 定义一个队列，在广度优先搜索时，该队列存储已被访问的路径长度为1，2，…的顶点；
• 定义访问函数visit()、深度优先搜索函数DFS()和广度优先搜索函数BFS()；
• 主函数实现各函数的调用。

三、 实验工具

Dev-C++

四、 实验代码

//Authors:xiaobei
#include<stdio.h>
#include<stdlib.h>
#define MaxInt 32767
#define MVNum 100
typedef char VerTexType;
typedef int ArcType;
//定义图结构
typedef struct{
 VerTexType vexs[MVNum];
 ArcType arcs[MVNum][MVNum];
 int vexnum,arcnum;
}AMGraph;
//定义辅助链队
typedef struct QNode{
 char data;
 struct QNode *next;
}QNode,*QueuePtr;
typedef struct{
 QueuePtr front;
 QueuePtr rear;
}LinkQueue;
//定义全局辅助数组visited[MVNum]
int visited[MVNum];
//函数返回定点下标
int LocateVex(AMGraph G,char v){
 int i;
 for(i=0;i<G.vexnum;i++)
  if(G.vexs[i]==v)
   return i;
  return -1;
}
//函数访问并输出顶点，返回下标
int visit(AMGraph G,char v){
 int i;
 for(i=0;i<G.vexnum;i++)
  if(v==G.vexs[i])
   printf("%c",v);
 return LocateVex(G,v);
}
//函数创建无向图，以邻接矩阵形式
int CreateUDN(AMGraph &G){
 int i,j,k,v1,v2,w;
 printf("[输入总顶点数和边数:]\n>>>");
 scanf("%d %d",&G.vexnum,&G.arcnum);
 for(i=0;i<G.vexnum;i++)
 {
  getchar();
  printf("[依次输入各顶点的信息:]\n>>>");
  scanf("%c",&G.vexs[i]);
 }
 for(i=0;i<G.vexnum;i++)
  for(j=0;j<G.vexnum;j++)
   G.arcs[i][j] = MaxInt;
 for(k=0;k<G.arcnum;k++){
  getchar();
  printf("[输入一条边依附的顶点及权值:]\n>>>");
  scanf("%c %c %d",&v1,&v2,&w);
  i = LocateVex(G,v1);
  j = LocateVex(G,v2);
  G.arcs[i][j]=w;
  G.arcs[j][i]=G.arcs[i][j];
 }
 return 1;
}
//函数深度遍历连通图
void DFS_AM(AMGraph G,char v){
 int w,u;
 u = visit(G,v);
 visited[u] = 1;
 for(w=0;w<G.vexnum;w++){
  if((G.arcs[u][w]<MaxInt) && (!visited[w]))
   DFS_AM(G,G.vexs[w]);
 }
}
//函数初始化链队
void InitQueue(LinkQueue &Q){
 Q.front = Q.rear = (QNode*)malloc(sizeof(QNode));
 Q.front->next=NULL;
}
//函数数据进队
void EnQueue(LinkQueue &Q,char e){
 QueuePtr p;
 p = (QNode*)malloc(sizeof(QNode));
 p->data = e;
 p->next = NULL;
 Q.rear->next=p;
 Q.rear = p;
}
//函数数据出队
void DeQueue(LinkQueue &Q,char &e){
 QueuePtr p;
 if(Q.front==Q.rear);
 else
 {
  p = Q.front->next;
  e = p->data;
  Q.front->next = p->next;
  if(Q.rear==p)
   Q.rear=Q.front;
  free(p);
 }
}
//函数判断链队是否为空
int QueueEmpty(LinkQueue Q){
 if(Q.front==Q.rear)
  return 1;
 else
  return 0;
}
//函数返回顶点下一个邻接点下标
int FirstAdjVex(AMGraph G,int c){
 int j;
 for(j=0;j<G.vexnum;j++)
  if(G.arcs[c][j]<MaxInt && visited[j]==0)
   return j;
  return -1;
}
//函数返回顶点下一个相对邻接点下标
int NextAdjVex(AMGraph G,int c,int w){
 int j;
 for(j=0;j<G.vexnum;j++)
  if(G.arcs[c][j]<MaxInt && visited[j]==0)
   return j;
  return -1;
}
//函数广度遍历连通图
void BFS_AM(AMGraph G,char v){
 int c,w,i;
 char u;
 LinkQueue Q;
 c = visit(G,v);
 visited[c] = 1;
 InitQueue(Q);
 EnQueue(Q,v);
 while(!QueueEmpty(Q)){
  DeQueue(Q,u);
  c = LocateVex(G,u);
  for(w=FirstAdjVex(G,c);w>=0;w=NextAdjVex(G,c,w))
  {
   if(!visited[w]){
    i = visit(G,G.vexs[w]);
    visited[i] = 1;
    EnQueue(Q,G.vexs[w]);
   }
  }
 }
}
//菜单打印
void Menu(){
 printf("\n————————菜单————————\n");
 printf("\n1.创建图结构;\n");
 printf("\n2.深度遍历（DFS）;\n");
 printf("\n3.广度遍历（BFS）;\n");
 printf("\n0.退出;\n");
 printf("\n——————————————————\n");
 printf("[请输入你的选择:]\n>>>");
}
//主函数
int main(){
 int i,user;
 char v;
 AMGraph G;
 while(1){
  Menu();
  scanf("%d",&user);
  switch(user){
  case 1:{
   CreateUDN(G);
   break;
  }
  case 2:{
   //初始化辅助数组
   for(i=0;i<G.vexnum;i++)
    visited[i] = 0;
   printf("[请输入遍历开始的顶点:]\n>>>");
   getchar();
   scanf("%c",&v);
   DFS_AM(G,v);
   break;
  }
  case 3:{
   //初始化辅助数组
   for(i=0;i<G.vexnum;i++)
    visited[i] = 0;
   printf("[请输入遍历开始的顶点:]\n>>>");
   getchar();
   scanf("%c",&v);
   BFS_AM(G,v);
   break;
  }
  case 0:{
   exit(0);
   break;
  }
  }
 }
 return 0;
}

五、 实验结果

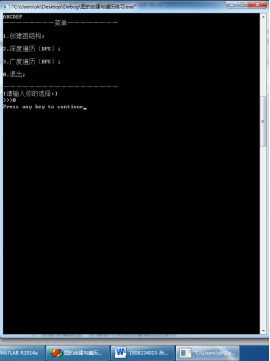
六、总结与思考

• 无向图的邻接矩阵是对称的，有向图邻接矩阵可能不对称。
• 深度优先搜索类似于栈结构的出栈于入栈过程，模拟递归，其实递归也是通过堆栈的形式实现的。
• 广度遍历是非递归过程，借助队列来实现。
• 辅助数组需要在全局使用，在主函数外定义。
• DFS与BFS空间复杂度都是O（n）,邻接矩阵时间复杂度都是O（n2），邻接表时间复杂度为O（n+e）。

邻接矩阵示意图：

以上就是C语言数据结构图的创建与遍历实验示例的详细内容，更多关于C语言图结构创建遍历的资料请关注我们其它相关文章！