Java数据结构之加权无向图的设计实现

2025-01-17 06:45:34

前言

加权无向图是一种为每条边关联一个权重值或是成本的图模型。这种图能够自然地表示许多应用。在一副航空图中，边表示航线，权值则可以表示距离或是费用。在一副电路图中，边表示导线，权值则可能表示导线的长度即成本，或是信号通过这条先所需的时间。此时我们很容易就能想到，最小成本的问题，例如，从西安飞纽约，怎样飞才能使时间成本最低或者是金钱成本最低？
在下图中，从顶点0到顶点4有三条路径，分别为0-2-3-4,0-2-4,0-5-3-4,那我们如果要通过那条路径到达4顶点最好呢？此时就要考虑，那条路径的成本最低。

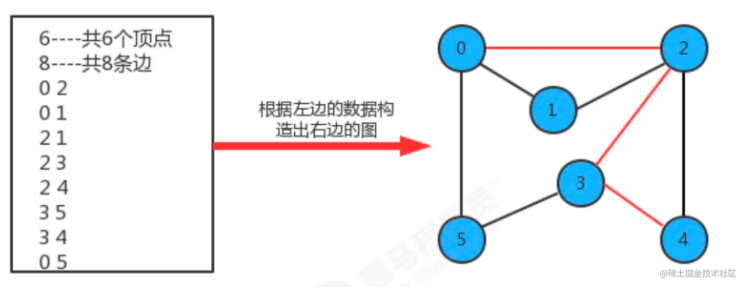
边的表示

加权无向图中的边我们就不能简单的使用v-w两个顶点表示了，而必须要给边关联一个权重值，因此我们可以使用对象来描述一条边。

API设计

类名	Edge implements Comparable
成员变量	1.private final int v：顶点一2.private final int w：顶点二3.private final double weight：当前边的权重
构造方法	Edge(int v,int w,double weight)：通过顶点v和w，以及权重weight值构造一个边对象
成员方法	1.public double weight():获取边的权重值2.public int either():获取边上的一个点3.public int other(int vertex)):获取边上除了顶点vertex外的另外一个顶点4.public int compareTo(Edge that)：比较当前边和参数that边的权重，如果当前边权重大，返回1，如果一样大，返回0，如果当前权重小，返回-1

代码实现

/**
 * 边
 *
 * @author alvin
 * @date 2022/11/3
 * @since 1.0
 **/
public class Edge implements Comparable<Edge> {
    //顶点一
    private final int v;
    //顶点二
    private final int w;
    //当前边的权重
    private final double weight;

    //通过顶点v和w，以及权重weight值构造一个边对象
    public Edge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    //获取边的权重值
    public double weight() {
        return weight;
    }

    //获取边上的一个点
    public int either() {
        return v;
    }

    //获取边上除了顶点vertex外的另外一个顶点
    public int other(int vertex) {
        if (vertex == v) {
            return w;
        } else {
            return v;
        }
    }

    @Override
    public int compareTo(Edge that) {
        //使用一个遍历记录比较的结果
        int cmp;

        if (this.weight() > that.weight()) {
            //如果当前边的权重值大，则让cmp=1；
            cmp = 1;
        } else if (this.weight() < that.weight()) {
            //如果当前边的权重值小，则让cmp=-1；
            cmp = -1;
        } else {
            //如果当前边的权重值和that边的权重值一样大，则让cmp=0
            cmp = 0;
        }

        return cmp;
    }
}

图的实现

之前我们已经完成了无向图，在无向图的基础上，我们只需要把边的表示切换成Edge对象即可。

API设计

类名	EdgeWeightedGraph
成员变量	1.private final int V: 记录顶点数量2.private int E: 记录边数量3.private Queue[] adj: 邻接表
构造方法	EdgeWeightedGraph(int V)：创建一个含有V个顶点的空加权无向图
成员方法	1.public int V():获取图中顶点的数量2.public int E():获取图中边的数量3.public void addEdge(Edge e):向加权无向图中添加一条边e4.public Queue adj(int v)：获取和顶点v关联的所有边5.public Queue edges()：获取加权无向图的所有边

代码实现

/**
 * 加权无向图的实现
 *
 * @author alvin
 * @date 2022/11/3
 * @since 1.0
 **/
public class EdgeWeightedGraph {
    //顶点总数
    private final int V;
    //边的总数
    private int E;
    //邻接表
    private Queue<Edge>[] adj;

    //创建一个含有V个顶点的空加权无向图
    public EdgeWeightedGraph(int V) {
        //初始化顶点数量
        this.V = V;
        //初始化边的数量
        this.E = 0;
        //初始化邻接表
        this.adj = new Queue[V];
        for (int i = 0; i < adj.length; i++) {
            adj[i] = new ArrayDeque<>();
        }

    }

    //获取图中顶点的数量
    public int V() {
        return V;
    }

    //获取图中边的数量
    public int E() {
        return E;
    }

    //向加权无向图中添加一条边e
    public void addEdge(Edge e) {
        //需要让边e同时出现在e这个边的两个顶点的邻接表中
        int v = e.either();
        int w = e.other(v);

        adj[v].add(e);
        adj[w].add(e);

        //边的数量+1
        E++;
    }

    //获取和顶点v关联的所有边
    public Queue<Edge> adj(int v) {
        return adj[v];
    }

    //获取加权无向图的所有边
    public Queue<Edge> edges() {
        //创建一个队列对象，存储所有的边
        Queue<Edge> allEdges = new ArrayDeque<>();

        //遍历图中的每一个顶点，找到该顶点的邻接表，邻接表中存储了该顶点关联的每一条边
        //因为这是无向图，所以同一条边同时出现在了它关联的两个顶点的邻接表中，需要让一条边只记录一次；
        for (int v = 0; v < V; v++) {
            //遍历v顶点的邻接表，找到每一条和v关联的边
            for (Edge e : adj(v)) {
                if (e.other(v) < v) {
                    allEdges.add(e);
                }
            }
        }
        return allEdges;
    }
}

到此这篇关于Java数据结构之加权无向图的设计实现的文章就介绍到这了,更多相关Java加权无向图内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

Java数据结构之图的基础概念和数据模型详解

目录图的实际应用图的定义及分类图的相关术语图的存储结构邻接矩阵邻接表图的实现图的API设计代码实现图的实际应用在现实生活中,有许多应用场景会包含很多点以及点点之间的连接,而这些应用场景我们都可以用即将要学习的图这种数据结构去解决. 地图: 我们生活中经常使用的地图,基本上是由城市以及连接城市的道路组成,如果我们把城市看做是一个一个的点,把道路看做是一条一条的连接,那么地图就是我们将要学习的图这种数据结构. 图的定义及分类定义: 图是由一组顶点和一组能够将两个顶点相连的边组
Java数据结构之有向图的拓扑排序详解

目录前言拓扑排序介绍检测有向图中的环实现思路 API设计代码实现基于深度优先的顶点排序实现思路 API设计代码实现拓扑排序 API设计代码实现测试验证前言在现实生活中,我们经常会同一时间接到很多任务去完成,但是这些任务的完成是有先后次序的.以我们学习java 学科为例,我们需要学习很多知识,但是这些知识在学习的过程中是需要按照先后次序来完成的.从java基础,到 jsp/servlet,到ssm,到springboot等是个循序渐进且有依赖的过程.在学习jsp前要首先掌
Java实现无向图的示例详解

目录基本概念图的定义无向图的定义无向图的 API 无向图的实现方式邻接矩阵边的数组邻接表数组无向图的遍历深度优先搜索广度优先搜索后记基本概念图的定义一个图是由点集V={vi} 和 VV 中元素的无序对的一个集合E={ek} 所构成的二元组,记为G=(V,E),V中的元素vi叫做顶点,E中的元素 ek叫做边. 对于V中的两个点 u,v,如果边(u,v) 属于E,则称 u,v两点相邻,u,v称为边(u,v)的端点. 我们可以用m(G)=|E| 表示图G中的边数,用n(G)
Java数据结构之有向图设计与实现详解

目录前言定义及相关术语 API设计代码实现前言在实际生活中,很多应用相关的图都是有方向性的,最直观的就是网络,可以从A页面通过链接跳转到B页面,那么a和b连接的方向是a->b,但不能说是b->a,此时我们就需要使用有向图来解决这一类问题,它和我们之前学习的无向图,最大的区别就在于连接是具有方向的,在代码的处理上也会有很大的不同. 定义及相关术语定义: 有向图是一副具有方向性的图,是由一组顶点和一组有方向的边组成的,每条方向的边都连着一对有序的顶点. 出度: 由某个顶点指出的边的个数
Java数据结构之图的两种搜索算法详解

目录前言深度优先搜索算法 API设计代码实现广度优先搜素算法 API设计代码实现案例应用前言在很多情况下,我们需要遍历图,得到图的一些性质,例如,找出图中与指定的顶点相连的所有顶点,或者判定某个顶点与指定顶点是否相通,是非常常见的需求. 有关图的搜索,最经典的算法有深度优先搜索和广度优先搜索,接下来我们分别讲解这两种搜索算法. 学习本文前请先阅读这篇文章 [数据结构与算法]图的基础概念和数据模型. 深度优先搜索算法所谓的深度优先搜索,指的是在搜索时,如果遇到一个结点既有子结点,
Java数据结构之图的路径查找算法详解

目录前言算法详解实现 API设计代码实现前言在实际生活中,地图是我们经常使用的一种工具,通常我们会用它进行导航,输入一个出发城市,输入一个目的地城市,就可以把路线规划好,而在规划好的这个路线上,会路过很多中间的城市.这类问题翻译成专业问题就是: 从s顶点到v顶点是否存在一条路径?如果存在,请找出这条路径. 例如在上图上查找顶点0到顶点4的路径用红色标识出来,那么我们可以把该路径表示为 0-2-3-4. 如果对图的前置知识不了解,请查看系列文章: [数据结构与算法]图的基础概念和数据
带你了解Java数据结构和算法之无权无向图

目录 1.图的定义 ①.邻接: ②.路径: ③.连通图和非连通图: ④.有向图和无向图: ⑤.有权图和无权图: 2.在程序中表示图 ①.顶点: ②.边: 3.搜索 ①.深度优先搜索(DFS) ②.广度优先搜索(BFS) ③.程序实现 4.最小生成树 5.总结 1.图的定义我们知道,前面讨论的数据结构都有一个框架,而这个框架是由相应的算法实现的,比如二叉树搜索树,左子树上所有结点的值均小于它的根结点的值,右子树所有结点的值均大于它的根节点的值,类似这种形状使得它容易搜索数据和插入数据,树的边表示
Java数据结构之加权无向图的设计实现

目录前言边的表示 API设计代码实现图的实现 API设计代码实现前言加权无向图是一种为每条边关联一个权重值或是成本的图模型.这种图能够自然地表示许多应用.在一副航空图中,边表示航线,权值则可以表示距离或是费用.在一副电路图中,边表示导线,权值则可能表示导线的长度即成本,或是信号通过这条先所需的时间.此时我们很容易就能想到,最小成本的问题,例如,从西安飞纽约,怎样飞才能使时间成本最低或者是金钱成本最低?在下图中,从顶点0到顶点4有三条路径,分别为0-2-3-4,0-2-4,0-5-3
常用的Java数据结构知识点汇总

目录 1.数据结构分类 2.线性数据结构 2.1数组 2.2可变数组 2.3链表 2.4栈 2.5队列 3.非线性数据结构 3.1树 3.2图 3.3散列表 3.4堆 1. 数据结构分类按照线性和非线性可以将Java数据结构分为两大类: ①线性数据结构:数组.链表.栈.队列②非线性数据结构:树.堆.散列表.图 2. 线性数据结构 2.1 数组数组是一种将元素存储于连续内存空间的数据结构,并且要求元素的类型相同. // 定义一个数组长度为5的数组array int[] array = new
Java数据结构与算法之栈(Stack)实现详解

本篇是java数据结构与算法的第2篇,从本篇开始我们将来了解栈的设计与实现,以下是本篇的相关知识点: 栈的抽象数据类型顺序栈的设计与实现链式栈的设计与实现栈的应用栈的抽象数据类型栈是一种用于存储数据的简单数据结构,有点类似链表或者顺序表(统称线性表),栈与线性表的最大区别是数据的存取的操作,我们可以这样认为栈(Stack)是一种特殊的线性表,其插入和删除操作只允许在线性表的一端进行,一般而言,把允许操作的一端称为栈顶(Top),不可操作的一端称为栈底(Bottom),同时把插入元素的操作
Java数据结构之图(动力节点Java学院整理)

1,摘要: 本文章主要讲解学习如何使用JAVA语言以邻接表的方式实现了数据结构---图(Graph).从数据的表示方法来说,有二种表示图的方式:一种是邻接矩阵,其实是一个二维数组:一种是邻接表,其实是一个顶点表,每个顶点又拥有一个边列表.下图是图的邻接表表示. 从图中可以看出,图的实现需要能够表示顶点表,能够表示边表.邻接表指是的哪部分呢?每个顶点都有一个邻接表,一个指定顶点的邻接表中,起始顶点表示边的起点,其他顶点表示边的终点.这样,就可以用邻接表来实现边的表示了.如顶点V0的邻接表如下: 与
Java数据结构与算法之树(动力节点java学院整理)

为什么使用树: 树结合了两种数据结构的有点:一种是有序数组,树在查找数据项的速度和在有序数组中查找一样快:另一种是链表,树在插入数据和删除数据项的速度和链表一样.既然这样,就要好好去学了.... (最主要讨论的是二叉树中的二叉搜索树,即一个节点的左子节点关键值小于这个节点,右子节点的关键值大于这个节点) 设计前的思考: 树-->元素(节点) class Node { public int iData ; public float fData ; public Node left ; public
Java数据结构与算法入门实例详解

第一部分:Java数据结构要理解Java数据结构,必须能清楚何为数据结构? 数据结构: Data_Structure,它是储存数据的一种结构体,在此结构中储存一些数据,而这些数据之间有一定的关系. 而各数据元素之间的相互关系,又包括三个组成成分,数据的逻辑结构,数据的存储结构和数据运算结构. 而一个数据结构的设计过程分成抽象层.数据结构层和实现层. 数据结构在Java的语言体系中按逻辑结构可以分为两大类:线性数据结构和非线性数据结构. 一.Java数据结构之:线性数据结构线性数据结构:常见的
Java数据结构学习之树

一.树 1.1 概念与线性表表示的一一对应的线性关系不同,树表示的是数据元素之间更为复杂的非线性关系. 直观来看,树是以分支关系定义的层次结构. 树在客观世界中广泛存在,如人类社会的族谱和各种社会组织机构都可以用树的形象来表示. 简单来说,树表示的是1对多的关系. 定义(逻辑结构): 树(Tree)是n( n>=0 )个结点的有限集合,没有结点的树称为空树,在任意一颗非空树中: 有且仅有一个特定的称为根(root)的结点 . 当n>1的时,其余结点可分为 m( m>0 ) 个互不相交的
Java数据结构之链表实现（单向、双向链表及链表反转）

前言之前学习的顺序表查询非常快,时间复杂度为O(1),但是增删改效率非常低,因为每一次增删改都会元素的移动.可以使用另一种存储方式-链式存储结构. 链表是一种物理存储单元上非连续.非顺序的存储结构.链表由一序列的结点(链表中的每一个元素成为结点)组成. 结点API设计: 类名 Node 构造方法 Node(T t,Node next) 创建Node对象成员变量 T item:存储数据 Node next :指向下一个结点结点类: public class Node<T>{ Node ne

Java数据结构之加权无向图的设计实现

目录

前言

边的表示

API设计

代码实现

图的实现

API设计

代码实现

相关推荐

随机推荐