opencv python 傅里叶变换的使用

理论

傅立叶变换用于分析各种滤波器的频率特性，对于图像，2D离散傅里叶变换（DFT）用于找到频域.快速傅里叶变换（FFT）的快速算法用于计算DFT.

于一个正弦信号，x(t)=Asin(2πft)，我们可以说 f 是信号的频率，如果它的频率域被接受，我们可以看到 f 的峰值.如果信号被采样来形成一个离散信号，我们得到相同的频率域，但是在[−π,π] or [0,2π]范围内是周期性的 (or [0,N] for N-point DFT).

可以将图像视为在两个方向上采样的信号.因此，在X和Y方向上进行傅里叶变换可以得到图像的频率表示.

更直观的是，对于正弦信号，如果振幅在短时间内变化得非常快，你可以说它是一个高频信号.如果它变化缓慢，它是一个低频信号,可以把同样的想法扩展到图片上,边和噪声是图像中的高频内容,如果振幅没有很大的变化，那就是低频分量.

Numpy中的傅里叶变换

np.fft.fft2()

第一个参数是输入图像，它是灰度图像

第二个参数是可选的，它决定了输出数组的大小,如果它大于输入图像的大小，则输入图像在计算FFT之前填充了0.如果它小于输入图像，输入图像将被裁剪,如果没有参数传递，输出数组的大小将与输入相同.

一旦得到结果，零频率分量（DC分量）将位于左上角。 如果要将其置于中心位置，则需要在两个方向上将结果移动N2.np.fft.fftshift(),一旦你找到频率变换，你就能找到大小谱.

代码:

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('img.jpg',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

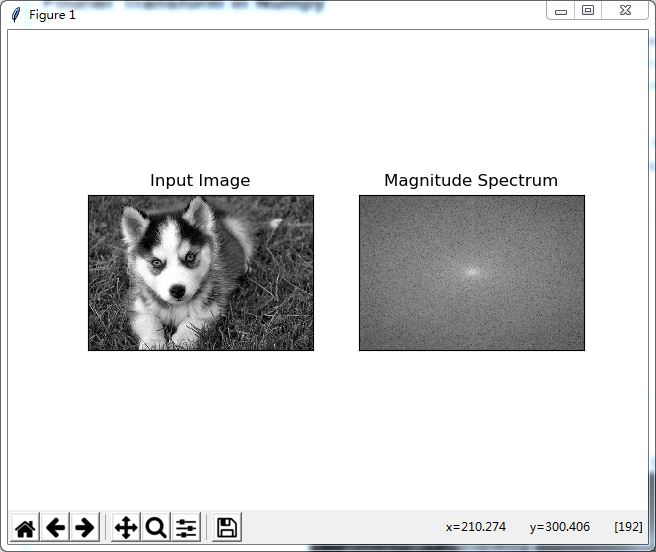
可以在中心看到更多的白色区域，表示低频率的内容更多.

现在可以在频域做一些运算，比如高通滤波和重建图像也就是找到逆DFT，只需用一个矩形窗口大小的60x60来移除低频部分，使用np.fft.ifftshift()应用反向移动，使DC组件再次出现在左上角,然后使用np.ifft2()函数找到反FFT,结果将会是一个复数,可以取它的绝对值.

代码:

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('img.jpg',0)

f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))

rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back)

plt.subplot(221),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(222),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(223),plt.imshow(img_back)
plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.subplot(224),plt.imshow(img_back, cmap = 'gray')
plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.show()

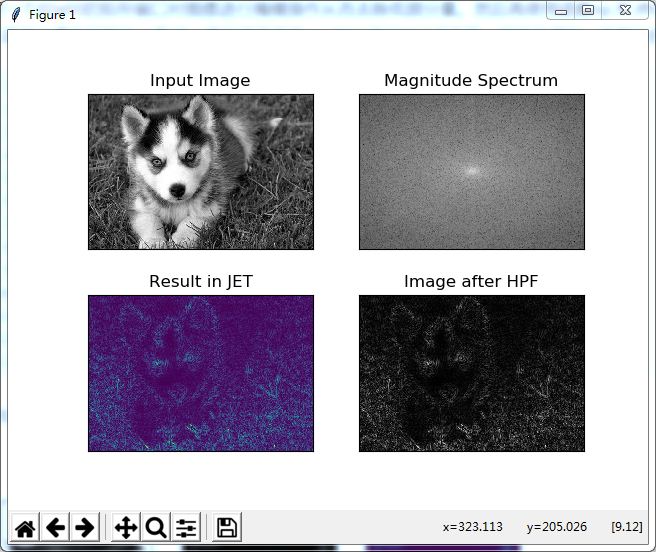
结果表明，高通滤波是一种边缘检测操作.

OpenCV中的傅里叶变换

OpenCV提供了cv.dft()和cv.idft()函数.它返回与前面相同的结果，但是有两个通道.第一个通道将会有结果的实部，第二个通道将会有一个虚部.

输入图像首先应该转换为np.float32

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('img.jpg',0)

dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)

magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

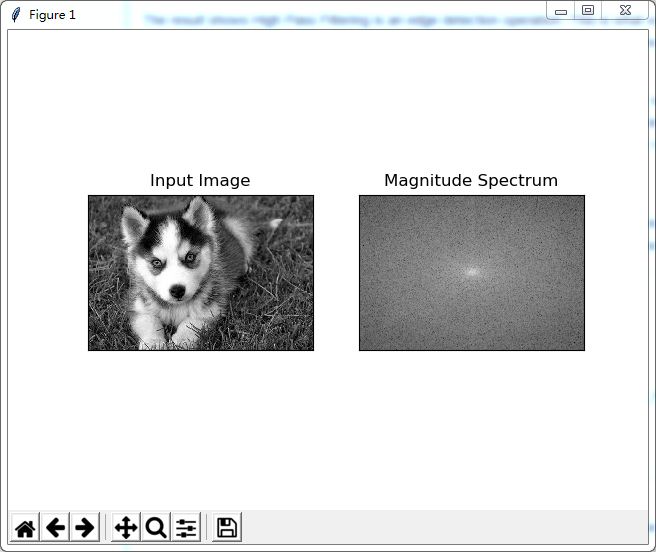
也可以使用cv.cartToPolar()，它可以在一次拍摄中同时返回大小和相位.

现在我们要做的是逆DFT.这次我们将移除图像中的高频内容，即我们将LPF应用到图像中.它实际上模糊了图像.为此，我们先创建一个具有高值(1)低频率的掩模，即我们通过低频内容，而在高频区域则是0。

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('img.jpg',0)

dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)

rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)

# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

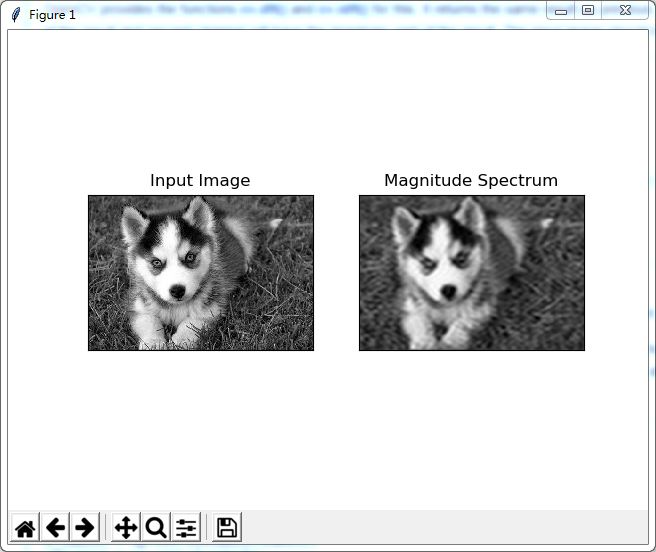
NOTE:

OpenCV函数cv.dft（）和cv.idft（）比Numpy函数更快.但是Numpy功能更加用户友好.

Fourier Transform

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。