python神经网络pytorch中BN运算操作自实现

BN 想必大家都很熟悉，来自论文：

《Batch Normalization Accelerating Deep Network Training by Reducing Internal Covariate Shift》

也是面试常考察的内容，虽然一行代码就能搞定，但是还是很有必要用代码自己实现一下，也可以加深一下对其内部机制的理解。

通用公式：

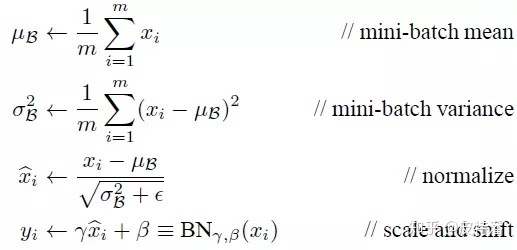
直奔代码：

首先是定义一个函数，实现BN的运算操作：

def batch_norm(is_training, x, gamma, beta, moving_mean, moving_var, eps=1e-5, momentum=0.9):
    # 判断当前模式是训练模式还是预测模式
    if not is_training:
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        x_hat = (x - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        if len(x.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = x.mean(dim=0)
            var = ((x - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。这里我们需要保持
            # x的形状以便后面可以做广播运算
            mean = x.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
            var = ((x - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
        # 训练模式下用当前的均值和方差做标准化
        x_hat = (x - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    x = gamma * x_hat + beta  # 拉伸和偏移
    return Y, moving_mean, moving_var

然后再定义一个类，就是常用的集成nn.Module的类了。

这里说明三点：

• 在卷积上的BN实现，是在 Batch，W，H上进行归一化操作的，也就是BWH拉成一个维度求均值和方差，均值和方差以及beta和gamma的尺寸为channel。当然其他各种N，包括IN，LN，GN都是包含WH维度的。
• 不需要计算梯度和参与梯度更新的参数，可以用self.register_buffer直接注册就可以了；注册的变量同样使用；
• 被包成nn.Parameter的参数，需要求梯度，但是不能加cuda（），否则会报错。 如果想在gpu上运算，可以将整个类的实例加.cuda（）。例如 bn = BatchNorm（**param），bn=bn.cuda().

class BatchNorm(nn.Module):
    def __init__(self, num_features, num_dims):
        super(BatchNorm, self).__init__()
        if num_dims == 2: # 同样是判断是全连层还是卷积层
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成0和1
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 不参与求梯度和迭代的变量，全初始化成0
        self.register_buffer('moving_mean', torch.zeros(shape))
        self.register_buffer('moving_var', torch.ones(shape))

    def forward(self, x):
        # 如果X不在内存上，将moving_mean和moving_var复制到X所在显存上
        if self.moving_mean.device != x.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var, Module实例的traning属性默认为true, 调用.eval()后设成false
        y, self.moving_mean, self.moving_var = batch_norm(self.training,
            x, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return x

以上就是python神经网络pytorch中BN运算操作自实现的详细内容，更多关于pytorch BN运算的资料请关注我们其它相关文章！