Java针对封装数组的简单复杂度分析方法

本文实例讲述了Java针对封装数组的简单复杂度分析方法。分享给大家供大家参考，具体如下：

完成了数组的封装之后我们还需对其进行复杂度分析：

此处的复杂度分析主要是指时间复杂度分析，算法的时间复杂度反映了程序执行时间随输入规模增长而增长的量级，在很大程度上能很好反映出算法的优劣与否。

1.简单概念

在各种不同算法中，若算法中语句执行次数为一个常数，则时间复杂度为O(1),另外，在时间频度不相同时，时间复杂度有可能相同，如T(n)=n2+3n+4与T(n)=4n2+2n+1它们的频度不同，但时间复杂度相同，都为O(n2)。 按数量级递增排列，常见的时间复杂度有：常数阶O(1),对数阶O(log2n),线性阶O(n), 线性对数阶O(nlog2n),平方阶O(n2)，立方阶O(n3),...， k次方阶O(nk),指数阶O(2n)。随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。相关图如下：

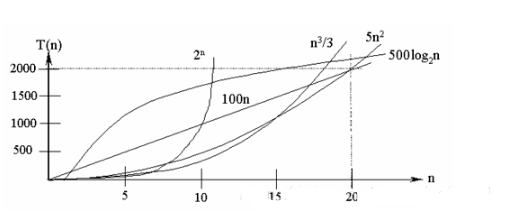
   从图中可见，我们应该尽可能选用多项式阶O(nk)的算法，而不希望用指数阶的算法。

见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜…＜Ο(2n)＜Ο(n!)

2.大O简单定义（非数学领域）

大O描述的是算法运行时间和输入数据之间的关系

3.简单程序时间复杂度分析

在上述中算法和n呈线性关系，那为什么要使用大O呢？称作O(n)?

其实上述的程序中，实际的实际时间复杂度：T = c1*n + c2，在这里忽略了常数c1和c2。

因此：算法和N呈线性相关，取n的高阶项，因为当n趋于无穷大的时候，低阶项起的作用很小。

4.对动态数组的时间复杂度进行分析

（1）动态数组添加操作时间复杂度分析

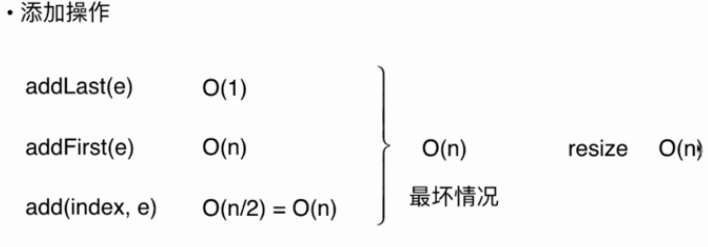
(1)addLast(e)方法 :只需在最后位置添加   时间复杂度 为O(1)

(2)addFirst(e)方法，数组中均需向后移动一位   时间复杂度 为O(n)

(3)add(index,e)方法，在index位置插入e,时间复杂度与选择的位置有关，选择最后时间复杂度 为O(1)；选择第一个位置时间复杂度 为O(n)；对于其他情况与概率有关，在平均情况下只需要移动n/2个位置   时间复杂度 为O(n/2)=O(n)

总的来说：数组添加的时间复杂度为O(n)（最坏情况考虑）

在添加的时候可能会触发resize方法，需要移动n个元素到新数组中   时间复杂度 为O(n)

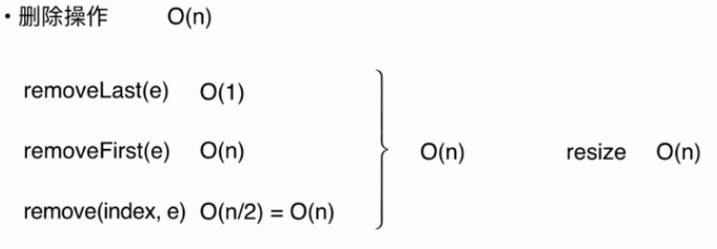
（2）动态数组删除操作时间复杂度分析

相同的分析方法，可以得出删除操作的时间复杂度

（3）动态数组修改操作时间复杂度分析

对于修改，只要通过索引找到即可进行修改，时间复杂度为O(1)

（4）动态数组查找操作时间复杂度分析

动态数组时间复杂度分析总结：

关于resize方法，我们完全使用最坏情况分析是不合理的，其分析情况我们将在下一节进行学习~

更多关于java相关内容感兴趣的读者可查看本站专题：《Java数组操作技巧总结》、《Java字符与字符串操作技巧总结》、《Java数学运算技巧总结》、《Java数据结构与算法教程》及《Java操作DOM节点技巧总结》

希望本文所述对大家java程序设计有所帮助。

赞 (0)

相关推荐

  • Java实现求子数组和的最大值算法示例

    Java实现求子数组和的最大值算法示例

    本文实例讲述了Java实现求子数组和的最大值算法.分享给大家供大家参考,具体如下: 一般C和C++在算法实现中使用较多,下面我们通过java语言实现算法,更有亲切感. 题目: 输入一个整形数组,数组里有正数也有负数. 数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和. 求所有子数组的和的最大值. 例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2, 因此输出为该子数组的和18. 实现代码: package arrDe

  • Java对数组实现选择排序算法的实例详解

    Java对数组实现选择排序算法的实例详解

    一. 算法描述     选择排序:比如在一个长度为N的无序数组中,在第一趟遍历N个数据,找出其中最小的数值与第一个元素交换,第二趟遍历剩下的N-1个数据,找出其中最小的数值与第二个元素交换......第N-1趟遍历剩下的2个数据,找出其中最小的数值与第N-1个元素交换,至此选择排序完成. 以下面5个无序的数据为例: 56 12 80 91 20(文中仅细化了第一趟的选择过程) 第1趟:12 56 80 91 20 第2趟:12 20 80 91 56 第3趟:12 20 56 91 80 第4趟

  • Java封装数组之改进为泛型数组操作详解

    本文实例讲述了Java封装数组之改进为泛型数组操作.分享给大家供大家参考,具体如下: 前言:通过上一节我们对我们需要封装的数组,进行了基本的增删改查的封装,但只局限于int类型的操作,为了能提供多种类型数组的操作,我们可以将其进一步封装为泛型数组. 1.定义泛型数组相关概念 (1)泛型数组让我们可以存放任何数据类型 (2)存放的类型不可以是基本数据类型,只能是类对象 基本类型: boolean.byte.char.short.int.long.float.double (3)每个基本数据类型都有

  • Java中打乱一个数组的2种公平算法分享

    公平算法,打乱数组 这是前几天面试的时候遇见的一道题目,看到这个题首先想到了洗牌程序: 方法一:洗牌程序原理 在java.util包中的Collections类中的 shuffle方法,现在手工实现以下代码如下: package test.ms; import java.util.Random; public class Redistribute2 { public static void main(String[] args) { //define the array int[] s = {1

  • Java封装数组之动态数组实现方法详解

    本文实例讲述了Java封装数组之动态数组实现方法.分享给大家供大家参考,具体如下: 前言:在此之前,我们封装的数组属于静态数组,也即数组空间固定长度,对于固定长度的数组当元素超过容量时会报数组空间不足.为了能更好的使用数组,我们来实现一个可以自动扩充容量的数组. 实现思路: 1.当数组容量达到事先定义值时创建一个空间是data数组两倍的newData数组(扩容): 2.把data数组中的元素全部赋值到newData数组中: 3.把data数组重新执行newData数组. 一.定义核心扩容方法 /

  • Java封装数组实现在数组中查询元素和修改元素操作示例

    本文实例讲述了Java封装数组实现在数组中查询元素和修改元素操作.分享给大家供大家参考,具体如下: 前言:在上一小节中,我们已经对如何往数组中添加一个元素的方法进行了编写,此节中我们就如何查询出数组中元素与修改元素的方法进行编写. 在数组中,数据是存储在私有变量data中的,若我们想知道打印输出一些关于data中数据相关信息,我们可以使用toString()方法,在java中,该方法需要每个类自定义重写实现,针对该类,自定义如下: @Override public String toString

  • java数据结构与算法之双向循环队列的数组实现方法

    本文实例讲述了java数据结构与算法之双向循环队列的数组实现方法.分享给大家供大家参考,具体如下: 需要说明的是此算法我并没有测试过,这里给出的相当于伪代码的算法思想,所以只能用来作为参考! package source; public class Deque { private int maxSize; private int left; private int right; private int nItems; private long[] myDeque; //constructor p

  • 详解Java数据结构和算法（有序数组和二分查找）

    一.概述 有序数组中常常用到二分查找,能提高查找的速度.今天,我们用顺序查找和二分查找实现数组的增删改查. 二.有序数组的优缺点 优点:查找速度比无序数组快多了 缺点:插入时要按排序方式把后面的数据进行移动 三.有序数组和无序数组共同优缺点 删除数据时必须把后面的数据向前移动来填补删除项的漏洞 四.代码实现 public class OrderArray { private int nElemes; //记录数组长度 private long[] a; /** * 构造函数里面初始化数组 赋值默

  • Java封装数组实现包含、搜索和删除元素操作详解

    本文实例讲述了Java封装数组实现包含.搜索和删除元素操作.分享给大家供大家参考,具体如下: 前言:在上一小节中我们已经会了如何获取和如何修改数组中的元素,在本小节中我们将继续学习如何判断某个元素是否在数组中存在.查询出某个元素在数组中的位置.以及删除数组中元素等方法的编写. 1.查找数组中是否包含元素e,返回true或false //查找数组中是否包含元素e public boolean contains(int e) { for (int i = 0; i < size; i++) { if

  • Java实现求数组最长子序列算法示例

    本文实例讲述了Java实现求数组最长子序列算法.分享给大家供大家参考,具体如下: 问题:给定一个长度为N的数组,找出一个最长的单调自增子序列(不一定连续,但是顺序不能乱) 例如:给定一个长度为8的数组A{1,3,5,2,4,6,7,8},则其最长的单调递增子序列为{1,2,4,6,7,8},长度为6. 思路1:第一眼看到题目,很多人肯定第一时间想到的是LCS.先给数组排个序形成新数组,然后再把新数组和原数组拿来求LCS,即可得到答案.这种解法很多人能想得到,所以就不再赘述. 思路2:按照思路1的

  • Java封装数组之添加元素操作实例分析

    本文实例讲述了Java封装数组之添加元素操作.分享给大家供大家参考,具体如下: 在上一小节中,我们对数组进行了一个基本的封装,该小节中,我们在上一次基础上,新增往数组添加元素的方法: 1.向所有元素后添加一个元素 思路: (1)先判断当前数组容量是否已满,未满则转入(2),否则抛出异常 (2)在元素下标为size的位置插入新元素 (3)维护我们的size值 //向所有元素后添加元素 public void addLast(int e) { if (size == data.length) thr

随机推荐