C++二叉树的创建及遍历详情

目录

• 树的定义
• 什么是树？
• 非递归的中序遍历的实现
• 二叉树的非递归的前序遍历的实现
• 二叉树的创建以及前中后序遍历的代码总结

树的定义

什么是树？

假如给我们一棵二叉树的前序遍历和中序遍历结果，我们应该如何通过这两个遍历结果创建一棵树呢？

通过前序遍历的结果我们可以找到二叉树的根节点，那么既然有了二叉树的根节点，我们在看中序遍历，在中序遍历中找到二叉树的根节点，呢么根节点之前的所有节点就是二叉树的左子树了，根节点之后的所有节点就是二叉树的右子树了。由此就可以对遍历结果进行分割了。

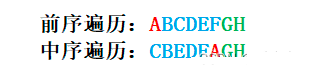
既然已经得到了左子树和右子树就好办了，我们知道二叉树的左子树和右子树也可以看作是一棵二叉树，此时二叉树的规模变小的了，但还是符合前序遍历和中序遍历的结果，所以可以对左右子树在分别进行创建。

伪代码表示：

BtNode* BuyNode()
{
    BtNode* s = (BtNode*)malloc(sizeof(BtNode));
    if(s == nullptr) return nullptr;
    memset(s,0,sizeof(BtNode));
    return s;
}
int FindPos(char* in,int n,char a)
{
    int pos  = -1;
    for(int i =0;i<n；++i)
    {
        if(in[i] == a)
        {
            pos = i;
            break;
        }
    }
    return pos;
}

BinaryTree CreateBinaryTree(char* Pre,char* in,int n)
{
    //首先我们需要购买一个节点，让其作为根节点，所以就需要一个购买节点函数
    BtNode* root = BuyNode();//购买节点
    root->value = pre[0];
    //要想构建二叉树，我们还需要在中序遍历中找到根节点的位置，从而确定左右子树，所以还需要一个查找函数，返回值是根节点的位置pos
    int pos = FindPos(in,n,pre[0]);//在中序遍历中查找pre[0]的位置,如果没有找到，说明两个遍历结果不是一棵二叉树，直接退出
    if(pos == -1) exit(0);
    //此时我们已经有了新的左子树和右子树，分别来创建
    CreateBinaryTree(左子树的前序遍历结果,左子树的中序遍历结果,左子树的大小);//创建左子树
    CreateBinaryTree(右子树的前序遍历结果,右子树的中序遍历结果,右子树的大小);//创建右子树
}
//pre 表示前序遍历数组，in表示中序遍历数组，n表示节点的个数
BinaryTree CreateBtree(char* Pre,char* in)
{
    int n = sizeof(pre)/sizeof(pre[0]);
    if(pre==nullptr||in==nullptr||n<=0)
    {
        return nullptr;//不满足以上条件说明不存在该二叉树，直接返回空指针
    }
    CreateBinaryTree(pre,in,n);//开始创建
}

构建二叉树以及使用递归方式前中后序遍历完整代码如下：

#include<iostream>
#include<stack>
#include<queue>
#include<memory>
/*
*二叉树的存储方式有两种，一种是以链表的方式进行存储，一种是以数组的方式进行存储
* 当以数组的方式进行存储的时候，要注意节点之间的关系，假设根节点的位置为POS那么左子树的位置就是
* 2*POS+1，右子树的位置就是2*POS+2。正是由于这层关系，当二叉树不是满二叉树的时候，使用数组进行存储
* 是非常的浪费空间的，空间的利用率较低。
* 当以链表的方式存储二叉树的时候，每一个二叉树节点都含有一个左孩子指针和一个右孩子指针，两个指针分别
* 指向相应的节点，节省空间，并且更容易使用。
*/
using namespace std;
typedef char ElemType;
typedef struct BtNode
{
	ElemType value;
	BtNode* leftchild;
	BtNode* rightchild;
}BtNode,*BinaryTree;
BtNode* BuyNode()
{
	BtNode* s = (BtNode*)malloc(sizeof(BtNode));
	if (s == NULL)return nullptr;
	memset(s, 0, sizeof(BtNode));
	return s;
}
int FindPos(ElemType* In, int n, ElemType val)
{
	int pos = -1;
	for (int i = 0; i < n ; ++i)
	{
		if (In[i] == val)
		{
			pos = i;
			break;
		}
	}
	return pos;
}
BinaryTree CreateBinTree(ElemType* Pr, ElemType* In, int n)
{
	BtNode* s = nullptr;
	if (n >= 1)
	{
		s = BuyNode();
		s->value = Pr[0];
		int pos = FindPos(In, n, Pr[0]);
		if (pos == -1) exit(0);

		s->leftchild = CreateBinTree(Pr + 1, In, pos);
		s->rightchild = CreateBinTree(Pr + pos + 1, In + pos + 1, n - pos - 1);
	}
	return s;
}
//通过前中序数组创建二叉树
BinaryTree CreateBinaryTree(ElemType* Pr, ElemType* In)
{
	int n = strlen(Pr);
	if (Pr == nullptr || In == nullptr)
	{
		return nullptr;
	}
	else
		return CreateBinTree(Pr, In, n);
}
BinaryTree CreateLI(ElemType* Li, ElemType* In, int n)
{
	BtNode* s = nullptr;
	if (n >= 1)
	{
		s = BuyNode();
		s->value = Li[n - 1];//后序遍历的最后一位数据是根节点
		int pos = FindPos(In, n, Li[n - 1]);
		if (pos == -1)exit(0);
		s->leftchild = CreateLI(Li, In, pos);
		s->rightchild = CreateLI(Li + pos, In + pos + 1, n - pos - 1);
	}

	return s;
}

//通过后中序数组建立二叉树
BinaryTree CreateLITree(ElemType* Li, ElemType* In)
{
	int n = strlen(Li);
	if (Li == nullptr || In == nullptr)
	{
		return nullptr;
	}
	else
		return CreateLI(Li, In, n);
}
//二叉树的前序遍历（递归方式）根节点-左子树-右子树
void PreOrder(BtNode* root)
{
	if (root != nullptr)
	{
		cout << root->value << " ";
		PreOrder(root->leftchild);
		PreOrder(root->rightchild);
	}
}
//二叉树的中序遍历（递归方式）左子树-根节点-右子树
void InOrder(BtNode* root)
{
	if (root != nullptr)
	{
		InOrder(root->leftchild);
		cout << root->value << " ";
		InOrder(root->rightchild);
	}
}
//二叉树的后序遍历（递归方式）左子树-右子树-根节点
void PastOrder(BtNode* root)
{
	if (root != nullptr)
	{
		InOrder(root->leftchild);
		InOrder(root->rightchild);
		cout << root->value << " ";
	}
}
int main()
{
	char ar[] = { "ABCDEFGH" };
	char br[] = { "CBEDFAGH" };
	char cr[] = { "CBEDFGHA" };
	//BinaryTree root = CreateBinaryTree(ar, br);
	BinaryTree root = CreateLITree(cr, br);
	PreOrder(root);
	cout << endl;
	InOrder(root);
	cout << endl;
	PastOrder(root);
	cout << endl;
}

非递归的中序遍历的实现

这里我们需要借助一个栈来实现，利用栈的特性，后进先出，当我们到达端节点时，打印端节点。按照中序的顺序，既左中右打印二叉树。具体怎么操作呢？

申请一个站用来存储节点，当根节点不为空，或者栈不为空的时候判断栈中节点的左孩子是否为空，如果左孩子不为空就继续将左孩子入栈，如果左孩子为空，就打印该节点，然后在访问右孩子，继续之前的判断。

要点在于我们访问每一个节点的时候，都要将其当做根节点来判断，将其当做一个小的二叉树，完成中序遍历，那么总的实现下来就是整个二叉树的中序遍历啦。

代码实现:

void NiceInOrder(BtNode* root)
{
	//如果根节点为空的话，直接返回就不用排序
	if(root == nullptr) return;
    std::stack<BtNode*> st;
    while(root!=nullptr || !st.empty())
    {
        //不断将左子树入栈，当左子树为空时，说明到达端节点
        while(root!=nullptr)
        {
            st.push(root);
            root = root->leftchild;
        }
        root = st.top(); st.pop();
        cout<< root->value;
        root = root->rightchild;
        }
    }
}

二叉树的非递归后序遍历：

后序遍历的顺序是左右中，优先访问左子树当左子树访问完毕之后，在访问右子树，最后访问根节点。那么非递归的后序遍历的难点在于，我们访问到端节点之后如何判断是否打印该节点呢，该节点是否还有右子树没有访问。

假设二叉树只有三个节点，如图所示：

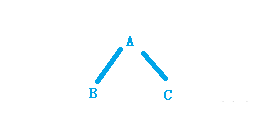
如果根节点不为空就将根节点入栈，因为是后序遍历，所以要再访问根节点的左子树，可以看到左子树也不为空，继续向左子树访问，当左子树为空时返回到根节点继续判断右子树是否为空，当左右子树都为空的时候，才能打印根节点。

代码实现：

void NicePastOrder(BtrNode* root)
{
    if(root == nullptr) return;
    std::stack<BtNode*> st;
    BtNode* tag = nullptr;//标志位，总是指向最近打印的那个节点
    while(root != nullptr || !st.empty())
    {
        while(root!=nullptr)
        {
            st.push(root);
            root = root->left;
        }
        //当上面的循环执行完毕，说明当前的*root已经指向了nullptr，那么他的双亲节点就是没有左子树的，然后可以进行出战操作了
        //当执行完出栈操作之后，我们就已经知道了root节点的左孩子是空的，或者左孩子已经打印过了。
        root= st.top(); st.pop();
        //因为执行的是后序遍历、出栈之后我们还需要判断，该节点是否有右子树，如果有并且还没有遍历，那么要将右子树遍历完毕才能打印根节点
        if(root->rightchild == nullptr || root->rightchild == tag)
        {
            cout << root->value;
            tag = ptr;
            ptr =nullptr;
        }
        else
        {
            //如果右子树不为空，就要再将右子树入栈，继续判断
            st.push(root);
            root = root->rightchild；
        }
    }
}

二叉树的非递归的前序遍历的实现

要实现前序遍历就需要先打印根节点，然后打印左子树再打印右子树，还是要使用分治的策略。使用一个栈，先将根节点入栈，只要root不为空或者栈不为空就一直循环，每次循环都出栈顶元素，并判断并将栈顶元素的左右孩子入栈。

代码实现：

void NicePreOrder(BtNode* root)
{
	if (root == nullptr) return;
	stack<BtNode*> s;
	s.push(root);//先将根节点放进去
	while (root != nullptr || !s.empty())
	{
		root = s.top(); s.pop();
		cout << root->value;
		if (root->rightchild != nullptr)
		{
			s.push(root->rightchild);
			root = root->rightchild;
		}
		if (root->leftchild != nullptr)
		{
			s.push(root->leftchild);
			root = root->leftchild;
		}
	}
}

二叉树的创建以及前中后序遍历的代码总结

#include<iostream>
#include<stack>
#include<queue>
#include<memory>
/*
*二叉树的存储方式有两种，一种是以链表的方式进行存储，一种是以数组的方式进行存储
* 当以数组的方式进行存储的时候，要注意节点之间的关系，假设根节点的位置为POS那么左子树的位置就是
* 2*POS+1，右子树的位置就是2*POS+2。正是由于这层关系，当二叉树不是满二叉树的时候，使用数组进行存储
* 是非常的浪费空间的，空间的利用率较低。
* 当以链表的方式存储二叉树的时候，每一个二叉树节点都含有一个左孩子指针和一个右孩子指针，两个指针分别
* 指向相应的节点，节省空间，并且更容易使用。
*/
using namespace std;
typedef char ElemType;
typedef struct BtNode
{
	ElemType value;
	BtNode* leftchild;
	BtNode* rightchild;
}BtNode,*BinaryTree;

BtNode* BuyNode()
{
	BtNode* s = (BtNode*)malloc(sizeof(BtNode));
	if (s == NULL)return nullptr;
	memset(s, 0, sizeof(BtNode));
	return s;
}

int FindPos(ElemType* In, int n, ElemType val)
{
	int pos = -1;
	for (int i = 0; i < n ; ++i)
	{
		if (In[i] == val)
		{
			pos = i;
			break;
		}
	}
	return pos;
}
BinaryTree CreateBinTree(ElemType* Pr, ElemType* In, int n)
{
	BtNode* s = nullptr;
	if (n >= 1)
	{
		s = BuyNode();
		s->value = Pr[0];
		int pos = FindPos(In, n, Pr[0]);
		if (pos == -1) exit(0);

		s->leftchild = CreateBinTree(Pr + 1, In, pos);
		s->rightchild = CreateBinTree(Pr + pos + 1, In + pos + 1, n - pos - 1);
	}
	return s;
}
//通过前中序数组创建二叉树
BinaryTree CreateBinaryTree(ElemType* Pr, ElemType* In)
{
	int n = strlen(Pr);
	if (Pr == nullptr || In == nullptr)
	{
		return nullptr;
	}
	else
		return CreateBinTree(Pr, In, n);
}

BinaryTree CreateLI(ElemType* In, ElemType* Li, int n)
{
	BtNode* s = nullptr;
	if (n >= 1)
	{
		s = BuyNode();
		s->value = Li[n - 1];//后序遍历的最后一位数据是根节点
		int pos = FindPos(In, n, Li[n - 1]);
		if (pos == -1)exit(0);
		s->leftchild = CreateLI( In,Li, pos);
		s->rightchild = CreateLI( In + pos + 1,Li + pos, n - pos - 1);
	}

	return s;
}

//通过后中序数组建立二叉树
BinaryTree CreateLITree(ElemType* In , ElemType* Li)
{
	int n = strlen(In );
	if (Li == nullptr || In == nullptr)
	{
		return nullptr;
	}
	else
		return CreateLI(In,Li , n);
}
//二叉树的前序遍历（递归方式）根节点-左子树-右子树
void PreOrder(BtNode* root)
{
	if (root != nullptr)
	{
		cout << root->value << " ";
		PreOrder(root->leftchild);
		PreOrder(root->rightchild);
	}
}

//二叉树的中序遍历（递归方式）左子树-根节点-右子树
void InOrder(BtNode* root)
{
	if (root != nullptr)
	{
		InOrder(root->leftchild);
		cout << root->value << " ";
		InOrder(root->rightchild);
	}
}

//二叉树的后序遍历（递归方式）左子树-右子树-根节点
void PastOrder(BtNode* root)
{
	if (root != nullptr)
	{
		InOrder(root->leftchild);
		InOrder(root->rightchild);
		cout << root->value << " ";
	}
}
二叉树的中序遍历（非递归方式）
//使用循环的方式一般是面试时考察的重点，原理是使用栈去存储相应的子树，当到达终端节点时，再将栈中的节点一一出栈
void NiceInOrder(BtNode* root)
{
	if (root == nullptr) return;
	stack<BtNode*> s;
	while (root !=nullptr || !s.empty())
	{
		//将整个左子树入栈
		while (root != nullptr)
		{
			s.push(root);
			root = root->leftchild;
		}
		//到达端节点时开始出栈
		root = s.top();
		s.pop();
		cout << root->value;
		root = root->rightchild;
	}
	cout << endl;
}
//二叉树的前序遍历（非递归方式）
void NicePreOrder(BtNode* root)
{
	if (root == nullptr) return;
	stack<BtNode*> s;
	BtNode* node = nullptr;
	s.push(root);
	while (!s.empty())
	{
		node = s.top();
		s.pop();
		cout << node->value;
		if (node->rightchild)
			s.push(node->rightchild);
		if (node->leftchild)
			s.push(node->leftchild);
	}
	cout << endl;
}

//二叉树的后序遍历（非递归方式）
void NicePastOrder(BtNode* root)
{
	if (root == nullptr)return;
	stack<BtNode*> st;
	BtNode* tag = nullptr;
	while (root != nullptr || !st.empty())
	{
		while (root != nullptr)
		{
			st.push(root);
			root = root->leftchild;
		}
		root = st.top();
		st.pop();
		if (root->rightchild == nullptr || root->rightchild == tag)
		{
			cout << root->value;
			tag = root;
			root = nullptr;
		}
		else
		{
			st.push(root);
			root = root->rightchild;
		}
	}
	cout << endl;
}
int main()
{
	char ar[] = { "ABCDEFGH" };
	char br[] = { "CBEDFAGH" };
	char cr[] = { "CEFDBHGA" };
	//BinaryTree root = CreateBinaryTree(ar, br);
	BinaryTree root = CreateLITree(br,cr );
	NiceInOrder(root);
	NicePreOrder(root);
	PreOrder(root);
	/*PreOrder(root);
	cout << endl;
	InOrder(root);
	cout << endl;
	PastOrder(root);
	cout << endl;*/
}

ightchild == tag)
{
cout << root->value;
tag = root;
root = nullptr;
}
else
{
st.push(root);
root = root->rightchild;
}
}
cout << endl;
}

int main()
{
char ar[] = { “ABCDEFGH” };
char br[] = { “CBEDFAGH” };
char cr[] = { “CEFDBHGA” };
//BinaryTree root = CreateBinaryTree(ar, br);
BinaryTree root = CreateLITree(br,cr );
NiceInOrder(root);
NicePreOrder(root);
PreOrder(root);
/PreOrder(root);
cout << endl;
InOrder(root);
cout << endl;
PastOrder(root);
cout << endl;/
}

到此这篇关于C++二叉树的创建及遍历详情的文章就介绍到这了,更多相关C++二叉树创建内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！