Python学习之MRO方法搜索顺序

目录

• 为什么会讲 MRO？
• 什么是 MRO
• 注意
• MRO 算法
• 什么是旧式类，新式类
• 想深入了解 C3 算法的可以看看官网
• 旧式类 MRO 算法
• 新式类 MRO 算法
• 新式 MRO 算法的问题
• 什么是单调性原则？
• C3 MRO 算法
• 简单了解下 C3 算法
• merge 的运算方式
• 简单类 MRO 的计算栗子
• 单继承MRO 的计算栗子
• 多继承MRO 的计算栗子
• 多继承MRO 的计算栗子二

为什么会讲 MRO？

• 在讲多继承的时候，有讲到， 当继承的多个父类拥有同名属性、方法，子类对象调用该属性、方法时会调用哪个父类的属性、方法呢？
• 这就取决于 Python 的 MRO 了

什么是 MRO

• MRO，method resolution order，方法搜索顺序
• 对于单继承来说，MRO 很简单，从当前类开始，逐个搜索它的父类有没有对应的属性、方法
• 所以 MRO 更多用在多继承时判断方法、属性的调用路径
• Python 中针对类提供了一个内置属性__mro__可以查看方法搜索顺序

实际代码

class A:
    def test(self):
        print("AAA-test")

class B:
    def test(self):
        print("BBB-test")

# 继承了三个类，B、A、还有默认继承的 object
class C(B, A):
    ...

# 通过类对象调用，不是实例对象！
print(C.__mro__)

# 输出结果
(<class '__main__.C'>, <class '__main__.B'>, <class '__main__.A'>, <class 'object'>)

• 1.在搜索方法时，是按照__mro__的输出结果从左往右的顺序查找的
• 2.如果在当前类（Class C）中找到方法，就直接执行，不再搜索
• 3.如果没有找到，就查找下一个类中（Class B）是否有对应的方法，如果找到，就直接执行，不再搜素
• 4.如果找到最后一个类（Class object）都没有找到方法，程序报错

类图

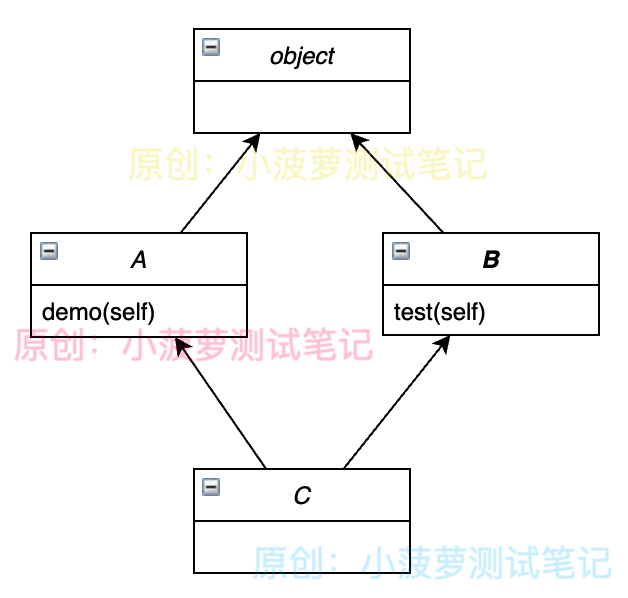
注意

其实 MRO 是涉及一个底层算法的，下面来详细讲解一下

MRO 算法

Python 发展到现在经历了三种算法

• 旧式类 MRO 算法：从左往右，采用深度优先搜索（DFS），从左往右的算法，称为旧式类的 MRO
• 新式类 MRO 算法：自 Python 2.2 版本开始，新式类在采用深度优先搜索算法的基础上，对其做了优化
• C3 算法：自 Python 2.3 版本，对新式类采用了 C3 算法；由于 Python 3.x 仅支持新式类，所以该版本只使用 C3 算法

什么是旧式类，新式类

Python学习之新式类和旧式类讲解

想深入了解 C3 算法的可以看看官网

https://www.python.org/download/releases/2.3/mro/

旧式类 MRO 算法

需要在 python2 环境下运行这段代码

实际代码

# 旧式类算法
class A:
    def test(self):
        print("CommonA")

class B(A):
    pass

class C(A):
    def test(self):
        print("CommonC")

class D(B, C):
    pass

D().test()

# python2 下的运行结果
CommonA

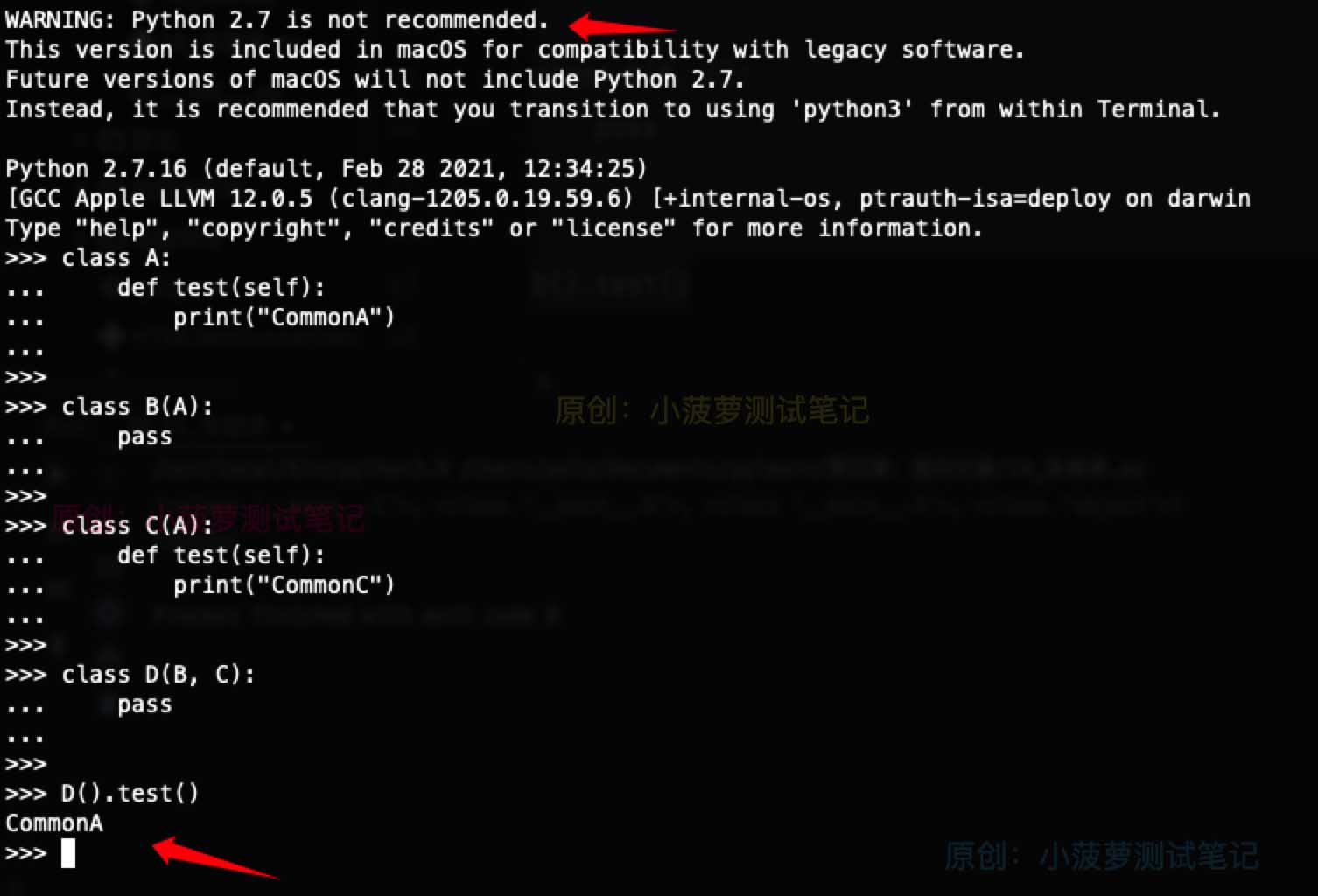
类图

分析

• 通过类图可以看到，此程序中的 4 个类是一个“菱形”继承的关系
• 当使用 D 类实例对象访问 test() 方法时，根据深度优先算法，搜索顺序为D->B->A->C->A
• 因此，旧式类 MRO 算法最先搜索得到 test() 方法是在 A 类里面，所以最终输出结果为 CommonA

新式类 MRO 算法

• 为解决旧式类 MRO 算法存在的问题，Python 2.2 版本推出了新的计算新式类 MRO 的方法
• 它仍然采用从左至右的深度优先遍历，但是如果遍历中出现重复的类，只保留最后一个

以上面的代码栗子来讲

• 深度优先遍历，搜索顺序为D->B->A->C->A
• 因为顺序中有 2 个 A，因此只保留最后一个
• 最终搜索顺序为D->B->C->A

新式 MRO 算法的问题

虽然解决了旧式 MRO 算法的问题，但可能会违反单调性原则

什么是单调性原则？

在子类存在多继承时，子类不能改变父类的 MRO 搜索顺序，否则会导致程序发生异常

实际代码

class X(object):
    pass

class Y(object):
    pass

class A(X, Y):
    pass

class B(Y, X):
    pass

class C(A, B):
    pass

深度优先遍历后的搜索顺序为：C->A->X->object->Y->object->B->Y->object->X->object

相同取后者的搜索顺序为：C->A->B->Y->X->object

分析不同类的 MRO

• A：A->X->Y->object
• B：A->Y->X->object
• C：C->A->B->X->Y->object

很明显，B、C 中间的 X、Y 顺序是相反的，就是说 B 被继承时，它的搜索顺序会被改变，违反了单调性

在 python2 中运行这段代码的报错

在 python3 中运行这段代码的报错

C3 MRO 算法

• 为解决前面两个算法的问题，Python 2.3 采用了 C3 方法来确定方法搜索顺序
• 多数情况下，如果别人提到 Python 中的 MRO，指的都是 C3 算法

将上面第一个栗子的代码放到 python3 中运行

class A:
    def test(self):
        print("CommonA")

class B(A):
    pass

class C(A):
    def test(self):
        print("CommonC")

class D(B, C):
    pass

D().test()

# 输出结果
CommonC

简单了解下 C3 算法

以上面代码为栗子，C3 会把各个类的 MRO 等价为以下等式

• A：L[A] = merge(A , object)
• B：L[B] = B + merge(L[A] , A)
• C：L[C] = C + merge(L[A] , A)
• D：L[D] = D + merge(L[B] , L[C] , B , C)

了解一下：头、尾

以 A 类为栗，merge() 包含的 A 成为 L[A] 的头，剩余元素（这里只有 object）称为尾

merge 的运算方式

• 1.将merge 第一个列表的头元素（如 L[A] 的头），记作 H
• 2.如果 H 出现在 merge 其他列表的头部，则将其输出，并将其从所有列表中删除
• 3.如果 H 只出现一次，那么也将其输出，并将其从所有列表中删除
• 4.如果 H 出现在 merge 其他列表的非头部，则取下一个列表的头元素记作 H，然后回到步骤二
• 5.最后回到步骤一，重复以上步骤

重复以上步骤直到列表为空，则算法结束；如果不能再找出可以输出的元素，则抛出异常

简单类 MRO 的计算栗子

class B(object): pass

print(B.__mro__)

(<class '__main__.B'>, <class 'object'>)

• MRO 计算方式

L[B] = L[B(object)]
     = B + merge(L[object])
     = B + L[object]
     = B object

单继承MRO 的计算栗子

# 计算 MRO
class B(object): pass

class C(B): pass

print(C.__mro__)

(<class '__main__.C'>, <class '__main__.B'>, <class 'object'>)

• MRO 计算方式

L[C] = C + merge(L[B])
     = C + L[B]
     = C B object

多继承MRO 的计算栗子

O = object

class F(O): pass

class E(O): pass

class D(O): pass

class C(D, F): pass

class B(D, E): pass

class A(B, C): pass

print(C.__mro__)
print(B.__mro__)
print(A.__mro__)

# 输出结果
(<class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <class 'object'>)
(<class '__main__.B'>, <class '__main__.D'>, <class '__main__.E'>, <class 'object'>)
(<class '__main__.A'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.D'>, <class '__main__.E'>, <class '__main__.F'>, <class 'object'>)

• O 类、object 类 MRO 计算

L[O] = O = object

• D、E、F 类 MRO 计算

L[D] = D + merge(L[O])
        = D O

• C 类 MRO 计算

L[C] = L[C(D, F)]
     = C + merge(L[D], L[F], DF)
     # 从前面可知 L[D] 和 L[F] 的结果
     = C +  merge(DO, FO, DF)
     # 因为 D 是顺序第一个并且在几个包含 D 的 list 中是 head，
     # 所以这一次取 D 同时从列表中删除 D
     = C + D + merge(O, FO, F)
     # 因为 O 虽然是顺序第一个但在其他 list (FO)中是在尾部, 跳过
     # 改为检查第二个list FO
     # F 是第二个 list 和其他 list 的 head
     # 取 F 同时从列表中删除 F
     = C + D + F + merge(O)
     = C D F O

• B 类 MRO 计算

L[B] = L[B(D, E)]
     = B + merge(L[D], L[E], DE)
     = B + merge(DO, EO, DE)
     = B + D + merge(O, EO, E)
     = B + D + E + merge(O)
     = B D E O

• A 类 MRO 计算

L[A] = L[A(B,C)]
        = A + merge(L[B], L[C], BC)
        = A + merge( BDEO, CDFO, BC )
        = A + B + merge( DEO, CDFO, C )
        # D 在其他列表 CDFO 不是 head，所以跳过到下一个列表的 头元素 C
        = A + B + C + merge( DEO, DFO )
        = A + B + C + D + merge( EO, FO )
        = A + B + C + D + E + merge( O, FO )
        = A + B + C + D + E + F + merge( O )
        = A B C D E F O

多继承MRO 的计算栗子二

O = object

class F(O): pass

class E(O): pass

class D(O): pass

class C(D, F): pass

class B(E, D): pass

class A(B, C): pass

print(C.__mro__)
print(B.__mro__)
print(A.__mro__)

# 输出结果
(<class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <class 'object'>)
(<class '__main__.B'>, <class '__main__.E'>, <class '__main__.D'>, <class 'object'>)
(<class '__main__.A'>, <class '__main__.B'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <class 'object'>)

• O 类、object 类 MRO 计算

L[O] = O = object

• D、E、F 类 MRO 计算

L[D] = D + merge(L[O])
        = D O

• C 类 MRO 计算

L[C] = L[C(D, F)]
        = C + merge(L[D], L[F], DF)
        = C + merge(DO, FO, DF)
        = C + D + merge(O, FO, F)
        = C + D + F + merge(O)
        = C D F O

• B 类 MRO 计算

L[B] = L[B(E, D)]
       = B + merge(L[E], L[D], ED)
       = B + merge(EO, DO, ED)
       = B + E + merge(O, DO, D)
       = B + E + D + merge(O)
       = B E D O

• A 类 MRO 计算

L[A]  = L[A(B, C)]
        = A + merge(L[B], L[C], BC)
        = A + merge(BEDO, CDFO, BC)
        = A + B + merge(EDO, CDFO, C)
        = A + B + E + merge(DO,CDFO, C)
        = A + B + E + C + merge(O,DFO)
        = A + B + E + C + D + merge(O, FO)
        = A + B + E + C + D + F + merge(O)
        = A B E C D F O

到此这篇关于Python学习之MRO方法搜索顺序的文章就介绍到这了,更多相关Python MRO方法搜索顺序内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！