Matlab实现黑洞优化算法的示例代码

目录

• 前言
• 1.概述
• 1.1黑洞算法
• 1.2黑洞搜索优化算法
• 1.3黑洞搜索算法的实现过程
• 2.Matlab代码实现
• 2.1主函数
• 2.2目标函数
• 2.3黑洞优化算法
• 3.结果展现

前言

应用的领域很多。

1.概述

1.1黑洞算法

根据黑洞现象原理首次提出BH 算法,它在传统PSO基础上引入了新的机制,有效地提高了收敛速度并防止了陷入局部极值的情况发生;但是该方法却没有提及如何确定黑洞边界和如何处理吸收星体的问题. Hatamlou BH算法进行了完善,让其更加接近于黑洞的自然现状,使其具有黑洞现象的一般特质.该方法不但沿袭了原BH算法的一切特性,同时还解决了原BH 算法的黑洞边界问题和吸收多余星点的问题.

1.2黑洞搜索优化算法

BH 算法的思想较为完整地描述了自然界中黑洞现象的一般特性;以BH 算法具有的这些特性为基础,BH算法的寻优搜索原理比较简单,易于实现.BH算法主要是模拟实际黑洞现象，在一定搜索空间内随机布置一定数量的星体,并通过统计学手段确定和评估搜索空间内每一个星体的适应度函数,选出一个具有最佳适应度值的星体作为黑洞.这个黑洞边界(以R为半径)被视为当前全局最优解所在区域,而黑洞本身被视为当前全局最优解;BH 算法中的黑洞具有与自然界黑洞同样的强吸引能力,在搜索域内所有其他星体都将向其靠拢且无法逃逸.星体被黑洞吸引并向黑洞靠拢的公式如下:

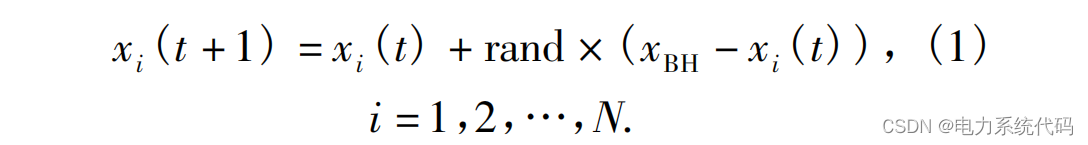
式中:x_i(t)和x_i+1(t+1)分别代表第i个星体在t和 t＋1次迭代时的位置;rand表示0,1]之间的随机数;Am是搜索空间内的黑洞位置;N是星体的数量.

在更替迭代过程中黑洞将进入其边界以内的星体一一吸收.每当一个星体被吸收的同时,在搜索空间内随机产生一个新的星体﹐星体的总数保持不变.黑洞边界范围计算公式如下:

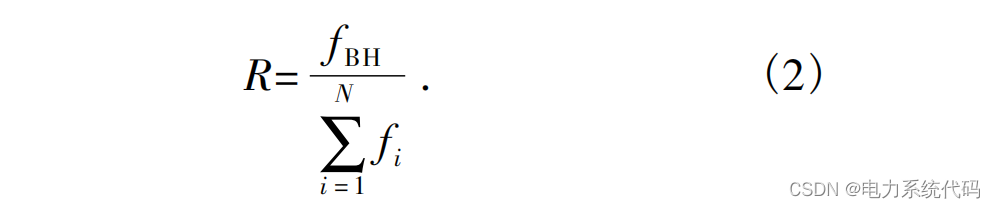
式中:f_BH是黑洞的适应度函数值;f_i是第i个星体的适应度函数值.

在被黑洞吸引的过程中,如果有一个星体i的适应度函数值f_i优于黑洞的适应度函数值f_BH则说明该黑洞所处位置并非最优,需要黑洞和星体互换位置.然后算法将以新生成的黑洞为中心继续运行下去，其他星体将通过位置更替公式(1)重新涌向新的黑洞位置,并被其吸收.

1.3黑洞搜索算法的实现过程

根据上述分析,得出黑洞算法的实现步骤:

步骤1初始化参数,在搜索空间内随机选取一定数量星体;

步骤2计算每个星体的适应度函数值;

步骤3选择一个具有最佳适应度值的星体作为黑洞;

步骤4根据式(1)更改每个星体的位置;

步骤5如果星体最优适应度函数值优于黑洞的适应度函数值,则交换二者位置;

步骤6 如果一个星体在黑洞的边界范围内,那么这个星体将被吸收﹐黑洞的边界半径由式(2)计算,同时,在搜索空间内随机产生一个新的星体;

步骤7当系统达到最大迭代次数,或者出现一个最好的适应度值时,程序停止运行,否则返回步骤4.

2.Matlab代码实现

2.1主函数

clear all
clc
close all
%% 初始化参数
d=5;                % 维度
options.lk=-32*ones(1,d);   % 下限
options.uk=32*ones(1,d);    % 上限
options.m=50; % 种群数量
options.MAXITER=500; % 最大迭代次数
options.n=length(options.uk);    % 问题的维度。
options.ObjFunction=@Ackley; % 调用目标函数
options.Display_Flag=1; % 在迭代中显示结果的标志
options.run_parallel_index=0;
options.run=10;

if options.run_parallel_index
    stream = RandStream('mrg32k3a');
    parfor index=1:options.run
        set(stream,'Substream',index);
        RandStream.setGlobalStream(stream)
        [bestX, bestFitness, bestFitnessEvolution,nEval]=BH_v1(options);
        bestX_M(index,:)=bestX;
        Fbest_M(index)=bestFitness;
        fbest_evolution_M(index,:)=bestFitnessEvolution;
    end
else
    rng('default')
    for index=1:options.run
        [bestX, bestFitness, bestFitnessEvolution,nEval]=BH_v1(options);
        bestX_M(index,:)=bestX;
        Fbest_M(index)=bestFitness;
        fbest_evolution_M(index,:)=bestFitnessEvolution;
    end
end

%% 可视化
[a,b]=min(Fbest_M);
figure
plot(1:options.MAXITER,fbest_evolution_M(b,:))
xlabel('迭代次数')
ylabel('适应度值')

fprintf(' MIN=%g  MEAN=%g  MEDIAN=%g MAX=%g  SD=%g \n',...
    min(Fbest_M),mean(Fbest_M),median(Fbest_M),max(Fbest_M),std(Fbest_M))
 

2.2目标函数

function [F, lb, ub, FGO] = Ackley(x)
%% 目标函数值
if (nargin==0)
    F=[];
    d=2;                % 维度
    lb=-32*ones(1,d);   % 下限
    ub=32*ones(1,d);    % 上限
    FGO=0;              % 总体最优值
else
    n=size(x,2);
    for ix=1:size(x,1)
        x0=x(ix,:);
        F(ix) = -20*exp(-0.2*sqrt(1/n*sum(x0.^2)))-...
                    exp(1/n*sum(cos(2*pi*x0)))+20+exp(1);
    end
end

2.3黑洞优化算法

function [bestX, bestFitness, bestFitnessEvolution,nEval]=BH_v1(options)
%--------------------------------------------------------------------------
% 黑洞优化算法
%--------------------------------------------------------------------------
% 在搜索空间中初始化具有随机位置的恒星群。
% 开始。
%   对于每一颗星，评估目标函数。
%   选择具有最佳适应值的最佳恒星作为黑洞。
%   根据公式更改每颗恒星的位置。
%   如果一颗恒星到达一个比黑洞成本更低的位置，交换它们的位置。
%   如果一颗恒星穿过黑洞的视界，在搜索空间中的随机位置用一颗新恒星替换它。
%   如果满足终止标准(最大迭代次数或足够好的适应度)，则退出循环。
% 结束循环
%--------------------------------------------------------------------------

ObjFunction=options.ObjFunction; % 目标函数的命名
n=options.n;    % 该问题的维度
uk=options.uk;   % 在第k维上界。
lk=options.lk;  % 在第k的下界。
m=options.m; % m：样本点数
MAXITER=options.MAXITER; % 最大迭代次数
nEval=0;
[x,xBH,iBH,ObjFunctionValue]=Initialize(options);
nEval=nEval+size(x,1);
for iteration =1:MAXITER
    %%  根据公式改变每颗星的位置。
    for i = 1 : m
        if i ~= iBH
            landa=rand;
            for k = 1 : n
                if landa<0.5
                    x(i,k)=x(i,k) + rand*(xBH(k)- x(i,k));
                else
                    x(i,k)=x(i,k) + rand*(xBH(k)- x(i,k));
                end
            end
        end
    end
    %% 如果恒星到达一个比黑洞成本低的位置，交换它们的位置
    ObjFunctionValue=feval(ObjFunction,x);
    nEval=nEval+size(x,1);
    %如果一颗恒星越过黑洞的事件视界，则在搜索空间中随机位置用一颗新恒星代替
    R=ObjFunctionValue(iBH)/sum(ObjFunctionValue);
    %     R=exp(-n*ObjFunctionValue(iBH)/sum(ObjFunctionValue))
    for i = 1 : m
        Distance(i)=norm(xBH- x(i,:));
    end
    [x,ObjFunctionValue]=NewStarGeneration(x,Distance,R,options,iBH,ObjFunctionValue);
    [x]=bound(x,lk,uk);
    [xBH,iBH]=argmin(x,ObjFunctionValue,options);

    %--------------------------------------------------------------------------------
    bestFitnessEvolution(iteration)=ObjFunctionValue(iBH);
    %--------------------------------------------------------------------------------

    if options.Display_Flag==1
        fprintf('迭代次数N为 %g 最优适应度为 %g\n',iteration,ObjFunctionValue(iBH))
    end

end
bestX=xBH;
bestFitness=ObjFunctionValue(iBH);
end

function [x,xBH,iBH,ObjFunctionValue]=Initialize(options)
ObjFunction=options.ObjFunction; % the name of the objective function.
n=options.n;    % n: dimension of the problem.
uk=options.uk;  % up: upper bound in the kth dimension.
lk=options.lk;  % lp: lower bound in the kth dimension.
m=options.m;    % m: number of sample points

for i = 1 : m
    for k = 1 : n
        landa=rand;
        x(i,k) = lk(k) + landa*(uk(k) - lk(k));
    end
end
% x(end+1,:)=x0;
ObjFunctionValue=feval(ObjFunction,x);
[index1,index2]=sort(ObjFunctionValue);
x=x(index2(1:m),:);
xBH=x(1,:);
iBH=1;
ObjFunctionValue=ObjFunctionValue(index2(1:m));
end

function [xb,ib,xw,iw]=argmin(x,f,options)
[minf,ib]=min(f);
xb=x(ib,:);
[maxf,iw]=max(f);
xw=x(iw,:);
end

function [x,ObjFunctionValue]=NewStarGeneration(x,Distance,R,options,iBH,ObjFunctionValue)
ObjFunction=options.ObjFunction;
n=options.n;
uk=options.uk;
lk=options.lk;
index=find(Distance<R);
for i=1:length(index)
    if index(i) ~= iBH
        for k = 1 : n
            x(i,k) = lk(k) + rand*(uk(k) - lk(k));
        end
        ObjFunctionValue(i)=feval(ObjFunction,x(i,:));
    end
end
end
function [x]=bound(x,l,u)
for j = 1:size(x,1)
    for k = 1:size(x,2)
        % 如果上限越界
        if x(j,k) > u(k),
            x(j,k) = u(k);
        end
        % 如果下限越界
        if x(j,k) < l(k),
            x(j,k) = l(k);
        end
    end
end
end

3.结果展现

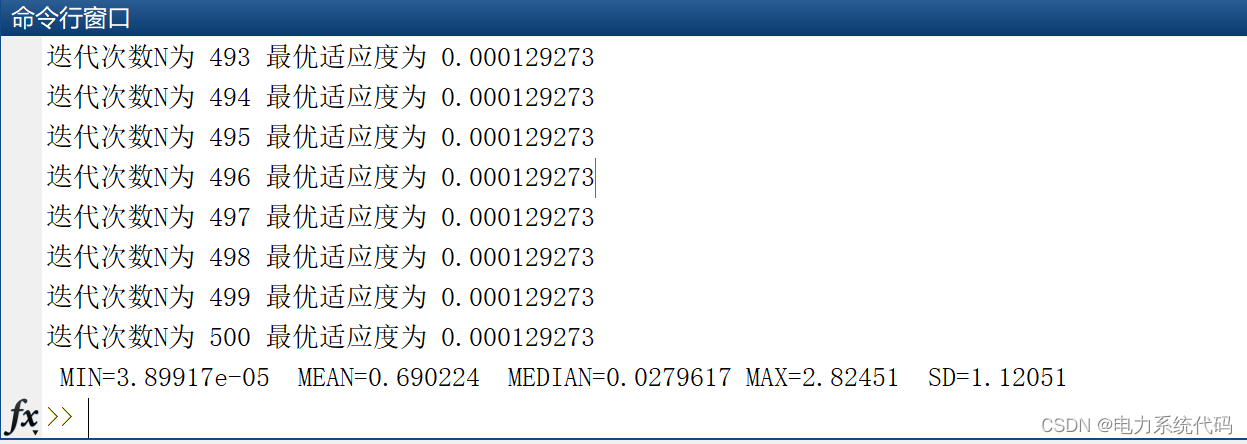
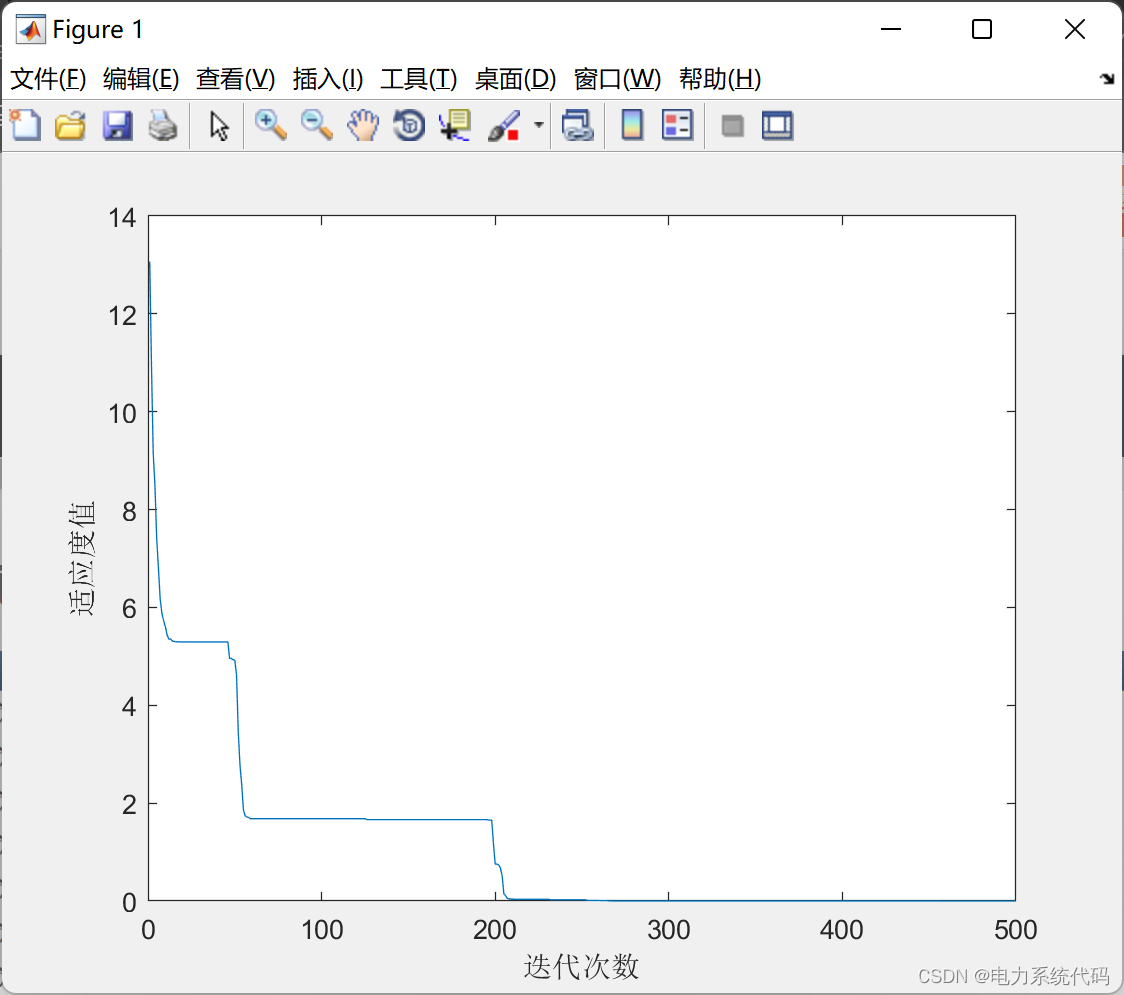
以上就是Matlab实现黑洞优化算法的示例代码的详细内容，更多关于Matlab黑洞优化算法的资料请关注我们其它相关文章！