Java深入了解数据结构之优先级队列(堆)

目录

• 一，二叉树的顺序存储
• ①存储方式
• ②下标关系
• ③二叉树顺序遍历
• 二，堆
• ①概念
• ②操作-向下调整
• ③建堆（建大堆为例）
• 三，堆的应用-优先级队列
• ①概念
• ②内部原理
• ③入队列
• ④出队列（优先级最高）
• ⑤返回队首元素（优先级最高）
• 四，堆排序

一，二叉树的顺序存储

①存储方式

使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。 一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。 这种方式的主要用法就是堆的表示。

②下标关系

已知双亲(parent)的下标，则：

左孩子(left)下标 = 2 * parent + 1;

右孩子(right)下标 = 2 * parent + 2;

已知孩子（不区分左右）(child)下标，则：

双亲(parent)下标 = (child - 1) / 2;

③二叉树顺序遍历

// 层序遍历
    void levelOrderTraversal(TreeNode root) {
        if(root == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode top = queue.poll();
            System.out.print(top.val+" ");
            if(top.left != null) {
                queue.offer(top.left);
            }
            if(top.right!=null) {
                queue.offer(top.right);
            }
        }
        System.out.println();
    }

二，堆

①概念

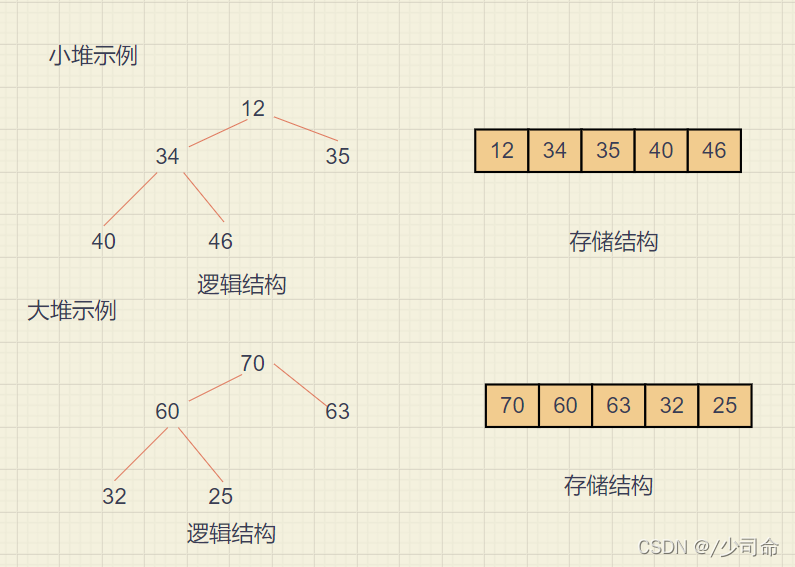
1. 堆逻辑上是一棵完全二叉树

2. 堆物理上是保存在数组中

3. 满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆

4. 反之，则是小堆，或者小根堆，或者最小堆

②操作-向下调整

前提：

左右子树必须已经是一个堆，才能调整。

说明：

1. array 代表存储堆的数组

2. size 代表数组中被视为堆数据的个数

3. index 代表要调整位置的下标

4. left 代表 index 左孩子下标

5. right 代表 index 右孩子下标

6. min 代表 index 的最小值孩子的下标 

过程（以小堆为例）：

Ⅰ index 如果已经是叶子结点，则整个调整过程结束

1. 判断 index 位置有没有孩子

2. 因为堆是完全二叉树，没有左孩子就一定没有右孩子，所以判断是否有左孩子

3. 因为堆的存储结构是数组，所以判断是否有左孩子即判断左孩子下标是否越界，即 left >= size 越界

Ⅱ 确定 left 或 right，谁是 index 的最小孩子 min

1. 如果右孩子不存在，则 min = left

2. 否则，比较 array[left] 和 array[right] 值得大小，选择小的为 min

Ⅲ比较 array[index] 的值 和 array[min] 的值，如果 array[index] <= array[min]，则满足堆的性质，调整结束

Ⅳ否则，交换 array[index] 和 array[min] 的值

Ⅴ然后因为 min 位置的堆的性质可能被破坏，所以把 min 视作 index，向下重复以上过程

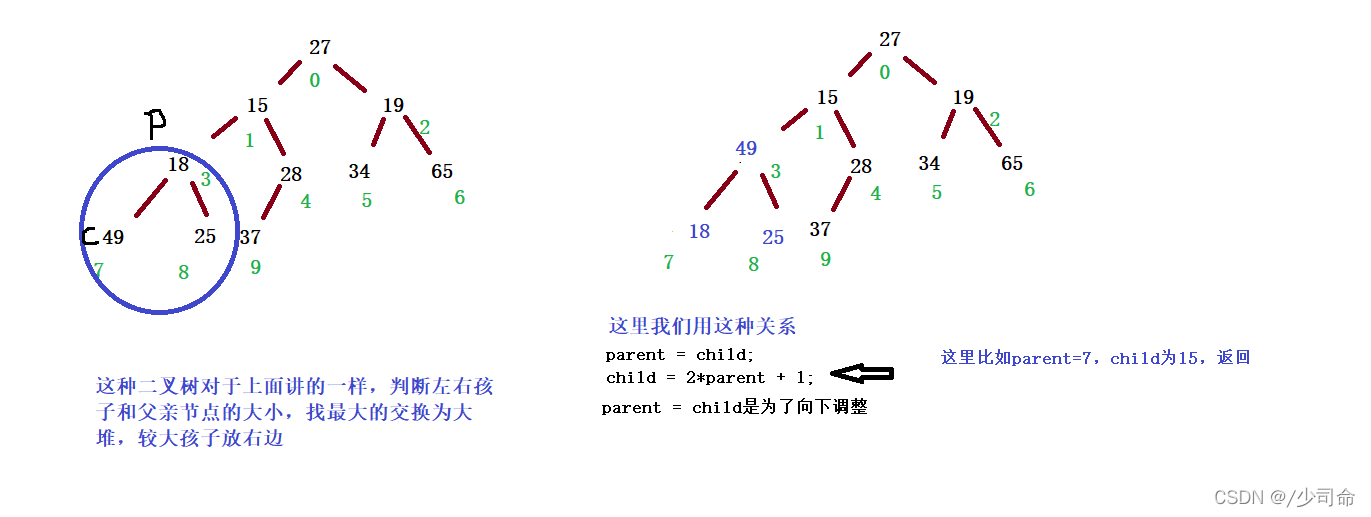
向下调整是以层序遍历的二叉树为例来遍历

public void adjustDown(int root,int len){
        int parent = root;
        int child = 2*parent + 1;
        while(child < len){
            if (child + 1 < len && this.elem[child] < this.elem[child + 1] ){
                child++;
            }
            if(this.elem[child] > this.elem[parent]){
                int tmp = this.elem[parent];
                this.elem[parent] = this.elem[child];
                this.elem[child] = tmp;
                parent = child;
                child = 2*parent + 1;
            }else{
                break;
            }
        }
    }

③建堆（建大堆为例）

下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构 建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的子树开始调整，一直 调整到根节点的树，就可以调整成堆。

//建大堆
    public void creatHeap(int[] array){
        for (int i = 0; i < array.length;i++){
            this.elem[i] = array[i];
            suedSize++;
        }
        for (int parent = (array.length - 1 - 1) / 2;parent >= 0;parent--){
            adjustDown(parent,this.suedSize);
        }

三，堆的应用-优先级队列

①概念

在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次 高的对象。最简单的一个例子就是，在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。 在这种情况下，我们的数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这 种数据结构就是优先级队列(Priority Queue)

②内部原理

优先级队列的实现方式有很多，但最常见的是使用堆来构建。

③入队列

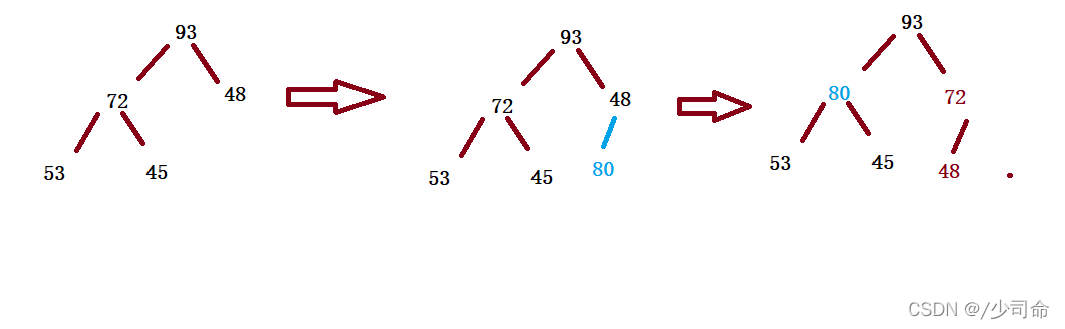
过程（以大堆为例）：

1. 首先按尾插方式放入数组

2. 比较其和其双亲的值的大小，如果双亲的值大，则满足堆的性质，插入结束

3. 否则，交换其和双亲位置的值，重新进行 2、3 步骤 4. 直到根结点

public void adjustUp(int child){
        int parent = (child - 1) / 2;
        while(child>0){
            if(this.elem[child] > this.elem[parent]){
                int tmp = this.elem[parent];
                this.elem[parent] = this.elem[child];
                this.elem[child] = tmp;
                child = parent;
                parent = (child - 1) / 2;
            }else {
                break;
            }
        }
    }

public void push(int val) {
        if (isFull()) {
            this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);
            this.elem[this.suedSize] = val;
            this.suedSize++;
            adjustUp(this.suedSize - 1);

        }
    }

④出队列（优先级最高）

为了防止破坏堆的结构，删除时并不是直接将堆顶元素删除，而是用数组的最后一个元素替换堆顶元素，然后通过向下调整方式重新调整成堆

 public boolean isEmpty(){
        return this.suedSize == 0;
    }

 public void pop(){
        if(isEmpty()){
            return;
        }
        int tmp = this.elem[0];
        this.elem[0] = this.elem[this.suedSize-1];
        this.elem[this.suedSize-1] = tmp;
        this.suedSize--;
        adjustDown(0,this.suedSize);
    }

⑤返回队首元素（优先级最高）

public int peek(){
        if(isEmpty()){
            return -1;
        }
        return this.elem[0];
    }

  public boolean isFull(){
        return this.suedSize == this.elem.length;
    }

四，堆排序

 /**
     * 一定是先创建大堆
     *      调整每棵树
     * 开始堆排序：
     *     先交换  后调整  直到 0下标
     */

    public void heapSort(){
        int end = this.suedSize-1;
        while (end > 0){
            int tmp = this.elem[0];
            this.elem[0] = this.elem[end];
            this.elem[end] = tmp;
            adjustDown(0,end);
            end--;

        }

    }

到此这篇关于Java深入了解数据结构之优先级队列(堆)的文章就介绍到这了,更多相关Java 优先级队列内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！